各种排序算法的简要记录(小白学习向)
第一次发博客,也是初学者,有错误请大胆指出,和谐讨论。
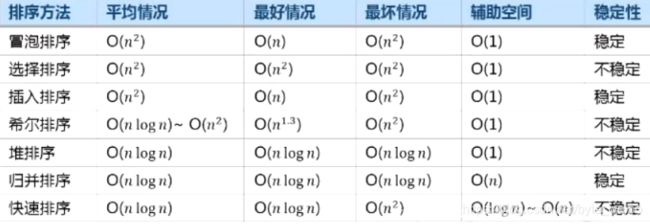
对七种排序算法的归纳总结:
一、冒泡排序
简述:以排升序为例,通过一个元素和该元素前面的一个元素比较,若该元素大于前方的元素,则交换二者。
重复上述步骤,直至无法交换。此时该组数据有序。
何时最快?(时间复杂度最小)
该组数据已经有序,虽然有序,但是冒泡排序需要遍历一边,发现每个元素都无法进行交换时结束,所以仍然需要O(N)的时间复杂度。
何时最慢?(时间复杂度最大)
该组数据与想要得到的顺序逆序,此时需要遍历并且交换N*N次,此时时间复杂度为O(N*N)(设一组降序的数据有n个元素,此时要将该组数据排成升序,因为每次只能交换2个元素,冒泡排序会进行n*n次遍历)
空间复杂度
需要开辟一个空间用于交换元素,所以是O(1)
稳定性
稳定。(冒泡排序不会将相等的元素进行交换,不会破坏其相对顺序)
二、选择排序
简述:以升序为例,首先在未排序序列中找到最小元素,存放到排序序列的起始位置。再从剩余未排序元素中继续寻找最小元素,然后放到已排序序列的末尾。
重复上述步骤,直至所有数据被排序完成。
时间复杂度
无论怎样,都需要O(N*N),因为无论是否有序,都会遍历n*n次。
空间复杂度
同冒泡排序,需要开辟一个空间用于交换元素,所以是O(1)
稳定性
不稳定。(选择排序可能会横跨交换,比如80a,80b,70,ab用来标记两个相同的数,运用选择排序改成升序,第一次会找到70,交换70和80a,变成70,80b,80a,此时破坏了相对顺序)
选择排序可以实现稳定,不过需要额外花费空间或者时间。
三、插入排序
简述:将前两个元素排序,看成一个单独的有序序列,去寻找下一个元素,放到有序序列中合适的位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面)
何时最快?(时间复杂度最小)
类似冒泡排序,数据已经有序,但仍需要遍历一边,发现每个元素都不需要变动其位置时结束,所以仍然需要O(N)的时间复杂度。
何时最慢?(时间复杂度最大)
当一组数据与想要得到的最终数据逆序,那么每放一个元素,会遍历有序序列一次,同时找到元素需要遍历所有数据,此时时间复杂度为O(N*N)
空间复杂度
同冒泡排序,需要开辟一个空间用于交换数据,所以是O(1)
稳定性
稳定。(待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。所以不会打乱相对位置)
四、希尔排序
简述:插入排序的进阶版,先进行预排序,之后进行插入排序,因为插入排序数据越接近有序,时间复杂度越小。
预排序:将待排序列划分为若干组,在每一组内进行插入排序,以使整个序列基本有序。
何时最快?(时间复杂度最小)
O(N^1.3)
具体咋算的我也不知道。。。。
何时最慢?(时间复杂度最大)
同插入排序,不过一般情况下会比O(N*N)要快。
空间复杂度
同插入排序,需要开辟一个空间用于交换数据,所以是O(1)
稳定性
不稳定。
以{3,7,8,6a,6b,5}为例
第一次分为3组,{3,6a},{7,6b},{8,5}
排序后变成{3,6a},{6b,7},{5,8}
放回去变成{3,6b,5,6a,7,8}
由此看出不稳定
五、堆排序
简述:利用建堆来达成排序。
将一个无序序列构造成了一个大堆, 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
最后得到一个有序序列。
时间复杂度
每次取堆的根结点为最大值,然后将最后一个节点作为根节点,进行堆调整,堆排序的时间等于建堆和进行堆调整的时间,所以堆排序的时间复杂度是O(nlog n + n) =O(nlog n)。
建堆的时间复杂度是O(n)。
排序的时间复杂度时O(nlog n)
空间复杂度
堆排序时就地排序,空间复杂度为O(1)
稳定性
不稳定。(当一个节点上他的子节点与其相等时,就会乱序)
六、归并排序
简述:利用递归,大事化小小事化了。
将一个序列不断分半(8=4+4=2+2+2+2=1+1+1+1+1+1+1+1),当分的只剩下一个元素时,认为他有序,之后在合上去进行排序。
举例说明:{65,94,23,48,63,9,3,98}
将其分为两组:{65,94,23,48},{63,9,3,98}
再分:{65,94},{23,48},{63,9},{3,98}
再分:{65},{94},{23},{48},{63},{9},{3},{98}
合上去同时排序:{65,94},{23,48},{9,63},{3,98}
合上去排序:{23,48,65,94},{3,9,63,98}
在合上去{3,9,23,48,63,65,94,98}
时间复杂度
一个长度为n的序列,分为log n层;每层排序时需要花费O(N)进行排序
最后时间复杂度为O(N*log N)
空间复杂度
归并排序的空间复杂度:
分层时创建的临时数组(log N层)
递归时压如栈的数据占用的空间:Nlog N;
所以空间复杂度N)
稳定性
稳定。(会按照顺序排序)
七、快速排序(挖坑法)
简述:挖个坑,埋点土…………
递归双指针。
举例说明:以{49,56,55,6,3,65,48}为例
挖坑挖坑,先要挖一个坑,找出第一个值“49”,成为基准值,将49的位置当成坑。
将坑的下一个元素的位置定位begin,最后一个元素的位置定位end。
while(end !=begin)
{
end不断--,找到比key小的值,这里我们直接找到“48”。将48放进坑里,此时end的位置成为坑。
注意这里是放进坑而不是交换。
之后begin不断++,找到比key大的值,这里找到了“56”,将“56”放进新的坑中。此时begin 的位置成为坑。
}
一直到end和begin相遇,此时end和begin指向的位置是一个坑,将我们最初找的基准值“49”放进坑里。数据变成:{ 48,3,6,49,55,65,56}
可以发现,49左边的都比49小,49右边的都比49大。以这里的49为中间值,将两边的数据分成两组,分别进行快速排序。递归调用重复步骤。最终实现数据有序。
何时最快?(时间复杂度最小)
类似归并排序,分成了log N层,每层处理需要O(N),此时时间复杂度为O(N log N)
何时最慢?(时间复杂度最大)
当选取的基准值凑巧是这段序列的最大值,此时快速排序变成了选择排序。
时间复杂度为O(N*N)
空间复杂度
每一次都平分数组的情况下:空间复杂度为O(log N) 。
但是会有特殊情况,在最差的情况下,每次只完成了一个元素,那么空间复杂度为 O(N)
稳定性
不稳定。
当两个数相等时,会因为实际的写法而不稳定。
当两个数相同时,会因为实际写法时究竟是大于基准值的数放在左边,还是大于等于基准值的数放在左边。
或者究竟是小于基准值的数放在右边,还是大于等于基准值的数放在右边。
如此,会导致乱序,并且无法在不消耗空间和时间的情况下避免该问题,所以不稳定。