基于MIV的神经网络变量筛选

1.案例背景

        一般神经网络中所包含的网络输人数据是研究者根据专业知识和经验预先选择好的,然而在许多实际应用中,由于没有清晰的理论依据,神经网络所包含的自变量即网络输入特征难以预先确定,如果将一些不重要的自变量也引入神经网络,会降低模型的精度,因此选择有意义的自变量特征作为网络输入数据常常是应用神经网络分析预测问题中很关键一步。选择神经网络输入的方法有多种,其基本思路是:尽可能将作用效果显著的自变量选入神经网络模型中,将作用不显著的自变量排除在外。本例将结合BP神经网络应用平均影响值(Mean Impact Value,MIV)算法来说明如何使用神经网络来筛选变量,找到对结果有较大影响的输人项,继而实现使用神经网络进行变量筛选。
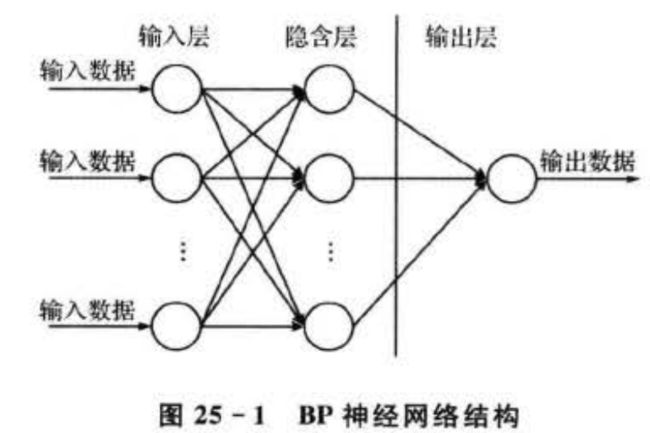
        BP(back propagation)神经网络是一种神经网络学习算法,其全称为基于误差反向传播算法的人工神经网络。图25-1所示为单隐藏层前馈网络拓扑结构，一般称为三层前馈网或三层感知器,即输入层,中间层(也称隐藏层)和输出层。输入层各神经元负责接收来自外界的输入信息,并传递给中间层各神经元;中间层是内部信息处理层,可以设计为单隐层或者多隐层结构;最后一个隐层传递到输出层各神经元的信息,经进一步处理后,完成一次学习的正向传播处理过程,由输出层向外界输出信息处理结果。BP神经网络的特点是:各层神经元仅与相邻层神经元之间相互全连接,同层内神经元之间无连接,各层神经元之间无反馈连接,构成具有层次结构的前馈型神经网络系统。单层前馈神经网络只能求解线性可分问题,能够求解非线性问题的网络必须是具有隐层的多层神经网络。当实际输出与期望输出不符时,进入误差的反向传播阶段。误差通过输出层,按误差梯度下降的方式修正各层权值,向隐层、输入层逐层反传。周而复始的信息正向传播和误差反向传播过程,是各层权值不断调整的过程,也是神经网络学习训练的过程,此过程一直进行到网络输出的误差减少到可以接受的程度﹐或者预先设定的学习次数为止。

        Dombi等人提出用MIV来反映神经网络中权重矩阵的变化情况,MIV被认为是在神经网络中评价变量相关性最好的指标之一,也为解决此类问题开创了新思路。因此探索此类型的评价指标在实际工作中的运用以及寻找新的评价指标是值得研究的课题。
        本例选择MIV作为评价各个自变量对于因变量影响的重要性大小指标。MIV是用于确定输人神经元对输出神经元影响大小的一个指标,其符号代表相关的方向,绝对值大小代表影响的相对重要性。具体计算过程:在网络训练终止后,将训练样本P中每一自变量特征在其原值的基础上分别加和减10%构成两个新的训练样本P，和P. ,将P,和P:分别作为仿真样本利用已建成的网络进行仿真,得到两个仿真结果A和A,求出A和A2的差值,即为变动该自变量后对输出产生的影响变化值(Impact Value,1V),最后将IⅣ按观测例数平均得出该自变量对于应变量——网络输出的MIV。按照上面步骤依次算出各个自变量的MIV值,最后根据MIV绝对值的大小为各自变量排序,得到各自变量对网络输出影响相对重要性的位次表,从而判断出输入特征对于网络结果的影响程度,即实现了变量筛选。

2.模型建立

        本例产生网络训练数据的方法如下:

3.MATLAB实现

 

%% 清空环境变量
clc
clear
%% 产生输入 输出数据

% 设置步长
interval=0.01;

% 产生x1 x2
x1=-1.5:interval:1.5;
x2=-1.5:interval:1.5;

% 产生x3 x4（噪声）
x=rand(1,301);
x3=(x-0.5)*1.5*2;
x4=(x-0.5)*1.5*2;

% 按照函数先求得相应的函数值，作为网络的输出。
F =20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2);

%设置网络输入输出值
p=[x1;x2;x3;x4];
t=F;


%% 变量筛选 MIV算法的初步实现（增加或者减少自变量）

p=p';
[m,n]=size(p);
yy_temp=p;

% p_increase为增加10%的矩阵 p_decrease为减少10%的矩阵
for i=1:n
    p=yy_temp;
    pX=p(:,i);
    pa=pX*1.1;
    p(:,i)=pa;
    aa=['p_increase'  int2str(i) '=p;'];
    eval(aa);
end


for i=1:n
    p=yy_temp;
    pX=p(:,i);
    pa=pX*0.9;
    p(:,i)=pa;
    aa=['p_decrease' int2str(i) '=p;'];
    eval(aa);
end


%% 利用原始数据训练一个正确的神经网络
nntwarn off;
p=yy_temp;
p=p';
% bp网络建立
net=newff(minmax(p),[8,1],{'tansig','purelin'},'traingdm');
% 初始化bp网络
net=init(net);
% 网络训练参数设置
net.trainParam.show=50;
net.trainParam.lr=0.05;
net.trainParam.mc=0.9;
net.trainParam.epochs=2000;

% bp网络训练
net=train(net,p,t);


%% 变量筛选 MIV算法的后续实现（差值计算）

% 转置后sim

for i=1:n
    eval(['p_increase',num2str(i),'=transpose(p_increase',num2str(i),');'])
end

for i=1:n
    eval(['p_decrease',num2str(i),'=transpose(p_decrease',num2str(i),');'])
end


% result_in为增加10%后的输出 result_de为减少10%后的输出
for i=1:n
    eval(['result_in',num2str(i),'=sim(net,','p_increase',num2str(i),');'])
end

for i=1:n
    eval(['result_de',num2str(i),'=sim(net,','p_decrease',num2str(i),');'])
end

for i=1:n
    eval(['result_in',num2str(i),'=transpose(result_in',num2str(i),');'])
end

for i=1:n
    eval(['result_de',num2str(i),'=transpose(result_de',num2str(i),');'])
end

%% MIV的值为各个项网络输出的MIV值 MIV被认为是在神经网络中评价变量相关的最好指标之一，其符号代表相关的方向，绝对值大小代表影响的相对重要性。


for i=1:n
    IV= ['result_in',num2str(i), '-result_de',num2str(i)];
    eval(['MIV_',num2str(i) ,'=mean(',IV,')'])
    
end

        运行结果如下：

MIV_1 =

    1.2030


MIV_2 =

    1.0120


MIV_3 =

   -0.0376


MIV_4 =

    0.0773

        MIV_n的值为各项网络输出的MIV值,MIV被认为是在神经网络应用中评价变量对结果影响大小的最好指标之一,其符号代表相关的方向,绝对值大小代表影响的相对重要性。
        由此可见;第一,二个变量得出的MIV值较大;因为F值是靠x1 ,x2计算出来的，与x3 ,x4无关,所以MIV筛选出的对结果有重要影响的自变量同真实情况一致。神经网络使用MIV方法对变量进行筛选是可行的。

4.案例扩展

        神经网络模型本身可以应用于多重共线性的数据,所谓多重共线性(multicollinearity)是指回归模型中的自变量之间由于存在精确相关关系或高度相关关系而使模型估计失真或难以估计准确。为了网络的训练效果更佳,使用了MIV算法来寻找对结果影响大的变量。不只是BP神经网络,其他很多神经网络在进行拟合,回归,分类的条件下,都可以应用MIV算法进行变量筛选并且建立自变量更少.效果更好的神经网络模型。