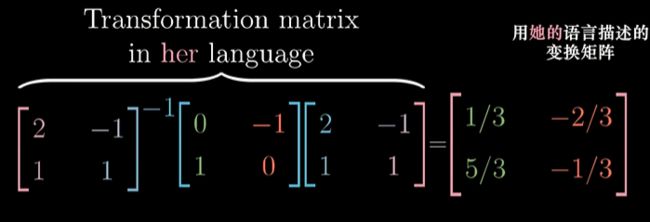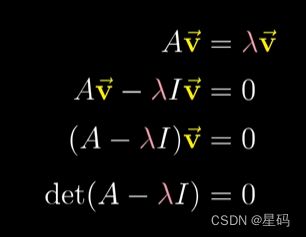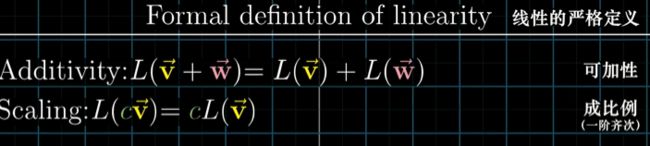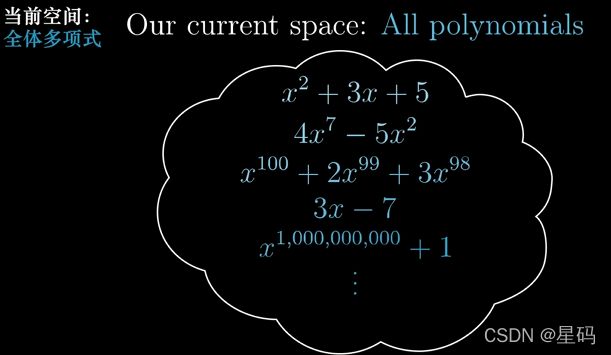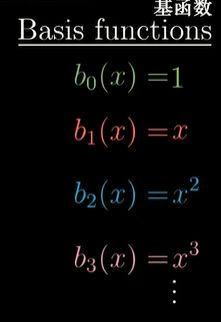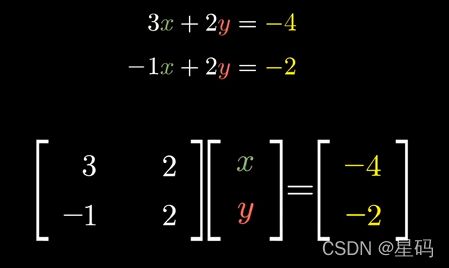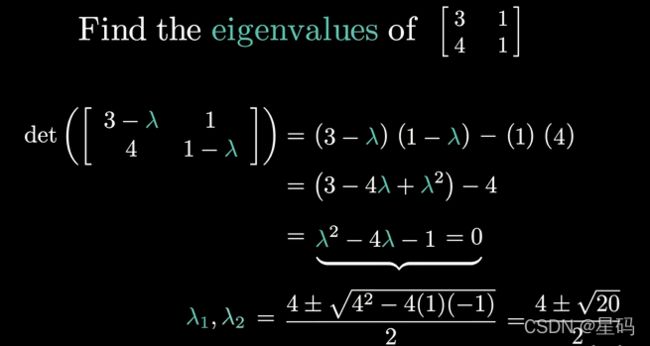线性代数的本质(第二部分)
线性代数的本质
- 七:基变换
-
- 1. 不同的基含义
- 2. 不同的基之间转换
-
- 2.1 从十字坐标系到新坐标系转化 --- 对新坐标系中向量 基于十字坐标系描述坐标( A A A)
- 2.2 从新坐标系到十字坐标系 --- 对十字坐标系中向量 基于新坐标系描述坐标( A − 1 A^{-1} A−1)
- 2.3 新坐标系与十字坐标系转化总结
- 2.4 基于新坐标系进行各种线性变换 --- 相似矩阵 A − 1 M A A^{-1}MA A−1MA
- 八:特征值与特征向量
-
- 1. 特征值与特征向量几何意义 --- 特征向量:变换后仍在张成空间的向量;特征值:衡量特征向量在变换中拉伸或缩放的比例
- 2. 特征值与特征向量作用 --- 矩阵描述的线性变换 新的理解角度
- 3. 特征值与特征向量计算思想 A v = λ v Av=\lambda v Av=λv --- 计算 d e t ( A − λ I ) = 0 det(A-\lambda I) = 0 det(A−λI)=0求特征值
- 4. 特征基 --- 基向量都是特征向量(对角矩阵); 变换有 足以张成全空间 的特征向量集合,那么就可以变换坐标系,使得特征向量就是基向量
- 九:抽象向量空间
-
- 0. 函数 与 向量 --- 有相同可加性 和 成比例
- 1. 线性变换的定义 --- 成比例 与 可加性
- 2. 用矩阵描述求导 --- 矩阵向量乘法 和 函数求导 联系
- 3. 向量空间与公理 --- 如果满足公理,就可以在其他奇怪的向量空间中使用已有结论
- 补1:克莱姆法则几何解释 --- 变换后向量与变换后基向量构成的面积(体积) 与 变化之前的比例 可以用 变换矩阵的行列式衡量
- 补2:计算二阶矩阵特征值的妙计 --- 与韦达定理联系
- 参考视频
前置知识 — 线性代数的本质一到六章:
矩阵和线性变换,矩阵与矩阵乘法,行列式,逆矩阵,列空间,零空间,点积与对偶性
博客链接:线性代数的本质(第一部分)
七:基变换
1. 不同的基含义
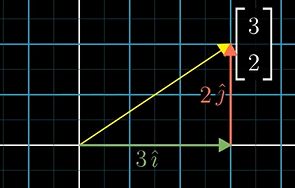
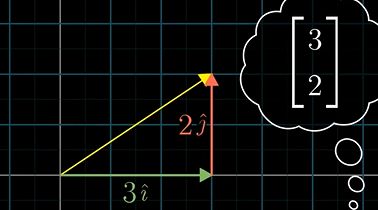
对于坐标,我们用更加线性代数的方法描述这个坐标:
将这些数看成拉伸或压缩向量的标量:对基向量进行伸缩
所选择的基就是坐标系 ( 1 , 0 ) , ( 0 , 1 ) (1,0),(0,1) (1,0),(0,1)含义的向量 — 规定各个方向的单位长度
不同的基表示:坐标轴的方向 与 网格间距 会有所不同
发生在向量 与 一组数(坐标) 之间任意一种转化被称为一个坐标系,其中有两个特殊的向量 i , j i,j i,j被称为基向量
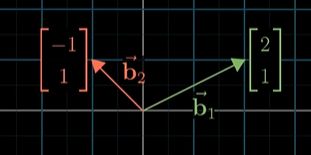
设:有一个我们通常了解的十字坐标系中的基向量 i , j i,j i,j,还有一个坐标系选取的是其他的基向量 b 1 , b 2 b_1,b_2 b1,b2
-
但以 b 1 , b 2 b_1,b_2 b1,b2为基向量看:
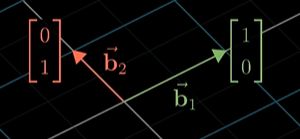
坐标为 ( 1 , 0 ) , ( 0 , 1 ) (1,0),(0,1) (1,0),(0,1),因为这两个向量就是定义这个坐标系 ( 1 , 0 ) , ( 0 , 1 ) (1,0),(0,1) (1,0),(0,1)含义的向量
这就使得相同的向量以不同的基来看是不同的坐标
∴ \therefore ∴ 当选择的基向量不同时:
- 同一个坐标描述的向量不同
- 同一个向量有不同的坐标描述
2. 不同的基之间转换
十字坐标系中有一对基向量 i , j i,j i,j
詹妮弗有一个新坐标系(异于十字坐标系),其有一对基向量 b 1 , b 2 b_1,b_2 b1,b2
2.1 从十字坐标系到新坐标系转化 — 对新坐标系中向量 基于十字坐标系描述坐标( A A A)
有一个向量,对于 异于十字坐标系的基向量 b 1 , b 2 b_1,b_2 b1,b2 来说的坐标系中,以 ( − 1 , 2 ) (-1,2) (−1,2)表示:
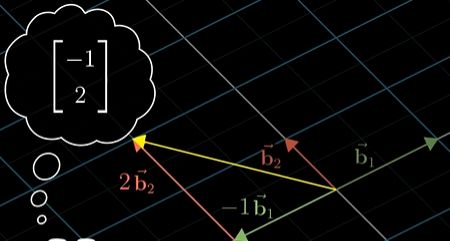
而从十字坐标系的角度来看: b 1 : ( 2 , 1 ) , b 2 : ( − 1 , 1 ) b_1:(2,1),b_2:(-1,1) b1:(2,1),b2:(−1,1)
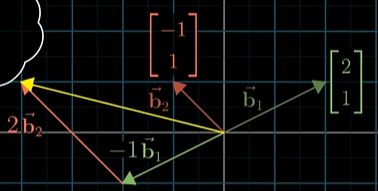
计算该向量 在十字坐标系中 坐标表示:
由第一章第1节知识知:
有向量 v v v,变换后的基向量 i , j i,j i,j的变成了向量 b 1 , b 2 b_1,b_2 b1,b2,利用变换前 v , i , j v , i , j v,i,j之间的线性组合,可以得到变换后的 v v v的坐标(变换后的向量的坐标仍然使用原始的十字坐标系表示的)
这里是将某个向量的特定坐标 ( − 1 , 2 ) (-1,2) (−1,2) 与 它的基向量 b 1 , b 2 b_1,b_2 b1,b2在十字坐标系表示的坐标 进行 数乘然后相加 来得到最后在十字坐标系中的向量坐标
而这个过程就是矩阵向量的乘法 — 该矩阵为基变换矩阵
- 矩阵的列代表以:十字坐标系 来描述 b 1 , b 2 b_1,b_2 b1,b2基向量
而矩阵乘法就是应用一个特定的线性变换(第一章第3节),以这个视角来看上式发生了什么:
- 这个矩阵将十字坐标系中的 ( 1 , 0 ) , ( 0 , 1 ) (1,0),(0,1) (1,0),(0,1)向量(即: i , j i,j i,j),线性变换为了新坐标系中的 ( 1 , 0 ) , ( 0 , 1 ) (1,0),(0,1) (1,0),(0,1)向量(即: b 1 , b 2 b_1,b_2 b1,b2)
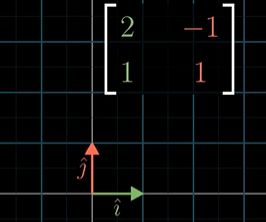

举个例子:
还是这个基变换矩阵 [ 2 − 1 1 1 ] \left[ \begin{matrix} 2 & -1\\ 1 & 1\end{matrix} \right] [21−11](即:相同的线性变换)
对于十字坐标系中所认为的 ( − 1 , 2 ) (-1,2) (−1,2)应用变换的意思:
利用线性变换的重要特性 — 变换前后的线性组合不变(第一章第1节)
∴ \therefore ∴ 这个基变换矩阵 [ 2 − 1 1 1 ] \left[ \begin{matrix} 2 & -1\\ 1 & 1\end{matrix} \right] [21−11]所做的事情是:
-
将我们的网格变换为了新坐标系的网格
将新坐标对向量的描述 转化为 十字坐标系的描述(因为新坐标下想要表达的向量: ( − 1 , 2 ) (-1,2) (−1,2),变成了基于十字坐标系下对该向量的坐标描述: ( − 4 , 1 ) (-4,1) (−4,1) ,即:将新坐标系中表示的向量坐标 变成 基于十字坐标系对该向量的坐标描述)
-
也可以这样理解:
将矩阵看成我们对新坐标中向量的误解 — 将十字坐标系中有相同坐标的向量,变成新坐标系真正想要表达的向量(描述的坐标 都是 基于十字坐标系的)
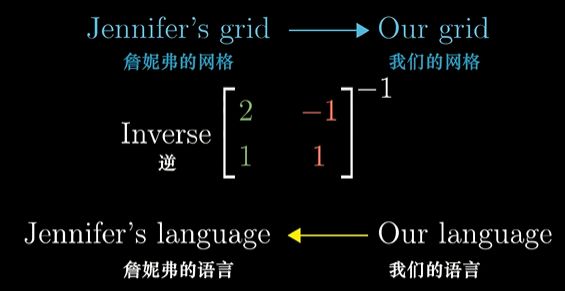
2.2 从新坐标系到十字坐标系 — 对十字坐标系中向量 基于新坐标系描述坐标( A − 1 A^{-1} A−1)
目的将:对 十字坐标系中的向量 计算出 其在新坐标系中的坐标
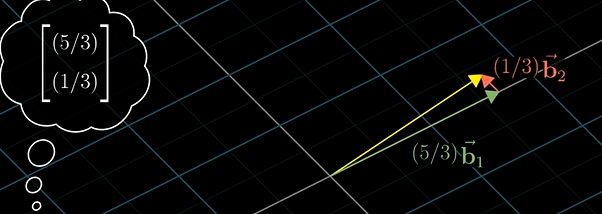
十字坐标系下的 ( 3 , 2 ) (3,2) (3,2)向量,在新坐标系下表示为 ( 5 / 3 , 1 / 3 ) (5/3,1/3) (5/3,1/3):
上一节中的 基变换矩阵 所做的是:
- 将新坐标系的语言转换为我们十字坐标系的语言(将新坐标系中表示的向量坐标 变成 基于十字坐标系对该向量的坐标描述)
而取这个基变换矩阵的逆,其意义相反:
计算其逆得到: [ 1 / 3 1 / 3 − 1 / 3 2 / 3 ] \left[ \begin{matrix} 1/3 & 1/3\\ -1/3 & 2/3\end{matrix} \right] [1/3−1/31/32/3]
相对本章第1节,这个基变换矩阵逆矩阵的意义是:将十字坐标系对向量的描述 转化为 新坐标对向量的描述
综上,如果想知道基于十字坐标系的某向量,例如十字坐标系下的 ( 3 , 2 ) (3,2) (3,2)向量,在新坐标系下表示为 ( 5 / 3 , 1 / 3 ) (5/3,1/3) (5/3,1/3):

2.3 新坐标系与十字坐标系转化总结
2.4 基于新坐标系进行各种线性变换 — 相似矩阵 A − 1 M A A^{-1}MA A−1MA
考虑线性变换,比如:逆时针旋转90°
用矩阵表示这个线性变换的时候,我们实际在追踪 i , j i,j i,j变换后的位置,变换后的坐标也就成了矩阵的列,即有旋转矩阵 [ 0 − 1 1 0 ] \left[ \begin{matrix} 0 & -1\\ 1 & 0\end{matrix} \right] [01−10]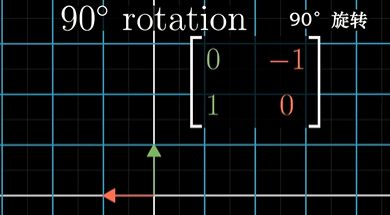
但这种表示与我们对基向量的选取密切相关,因为我们追踪 i , j i,j i,j,并且是在自己的坐标系中记录他们的去向
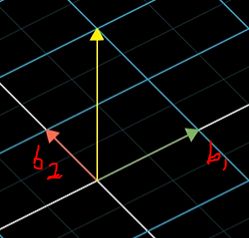
基于新坐标系 描述空间逆时针90°:
但旋转矩阵 [ 0 − 1 1 0 ] \left[ \begin{matrix} 0 & -1\\ 1 & 0\end{matrix} \right] [01−10]描述的是基于十字坐标系的 i , j i,j i,j的去向,并不是描述这个新坐标系的基的去向,且不是基于用新坐标系来表述坐标
总体思路总结:
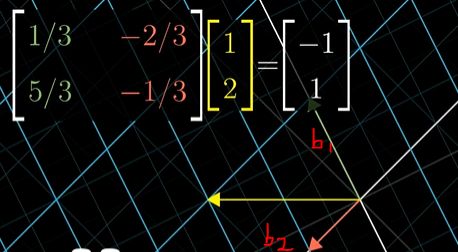
- 先将新坐标系表示的向量坐标 转化为 十字坐标系对该向量的描述,得到该向量基于十字坐标系的描述(因为我们知道基于十字坐标系的逆时针旋转对应的矩阵)
- 基于十字坐标系旋转90°的线性变换对应的矩阵 [ 0 − 1 1 0 ] \left[ \begin{matrix} 0 & -1\\ 1 & 0\end{matrix} \right] [01−10]
- 再将基于十字将 变换后的向量 转化到 新坐标系的描述
详细过程:
上面过程中可以得到式子: A − 1 M A A^{-1}MA A−1MA (相似矩阵),这三个矩阵的复合给出的就是 以新坐标系描述 的我们需要的变换;
相似矩阵 A − 1 M A A^{-1}MA A−1MA 其也暗示数学上一种转移作用:
- A − 1 A^{-1} A−1与 A A A 表示视角的转化 — 新旧坐标系转化
- 中间矩阵表示一种基于十字坐标系的变换
八:特征值与特征向量
1. 特征值与特征向量几何意义 — 特征向量:变换后仍在张成空间的向量;特征值:衡量特征向量在变换中拉伸或缩放的比例
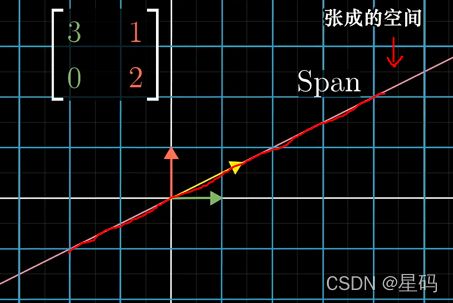
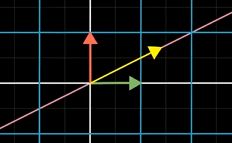
考虑二维空间中的线性变换:其将基向量 i , j i,j i,j变成了 ( 3 , 0 ) , ( 1 , 2 ) (3,0),(1,2) (3,0),(1,2),这个线性变换对应矩阵就为 [ 3 1 0 2 ] \left[ \begin{matrix} 3 & 1\\ 0 & 2\end{matrix} \right] [3012],之后关注其对某向量的作用
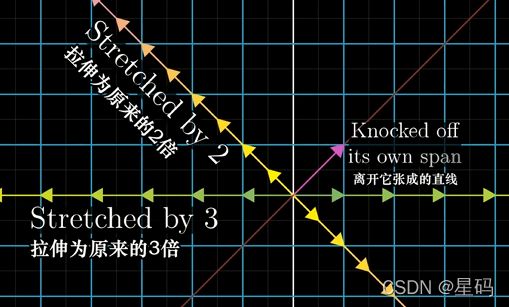
经过线性变换后,有的向量会离开它张成的空间
但有的向量比较特殊:
- 经过线性变化后,有的向量仍然留在其所张成的空间中
- 此时意味着矩阵对他的作用仅仅是拉伸或者压缩而已(因为这个向量变换后方向没有发生变换)
- 例子中,除了黄色向量,基向量 i i i也是这样一个特殊向量(变换后 i i i 仍留在 张成空间( x x x轴)中) — i i i变换后 变成了原来的3倍,仍留在 x x x轴
- 由图看出,黄色向量 变化后 成为原来2倍,线性性质暗示 — 处在该向量张成空间上的其他任何向量 也 仅仅被拉伸为原来2倍 — 同理:x轴上的向量都被拉伸为原来3倍
对于这个变换而言,拥有这一特殊性质(变换后仍在他们张成的空间中)的向量有:
对这些向量进行分析:由图可以看出,变换后,在 x x x轴的特殊的向量变成原来的3倍,在对角线上的向量变成原来的2倍,而其他的向量在变换后都离开了它张成的空间
特征值与特征向量:
2. 特征值与特征向量作用 — 矩阵描述的线性变换 新的理解角度
用途举例:
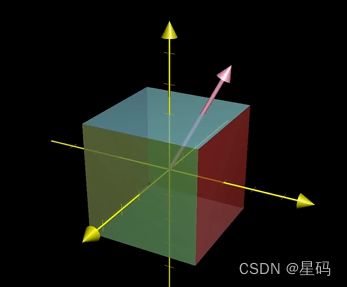
对三维空间的旋转,如果找到这个旋转的特征向量(即:留在其张成空间中的向量),那么就找到了旋转轴,特征向量对应特征值必须为1(因为旋转不缩放向量)
这样将 三维旋转看成了绕某个轴旋转 比 直接考虑这个变换对于 3 × 3 3 \times 3 3×3矩阵直观
对于任意矩阵描述的线性变换
- 可以使用其列描述变换后的基向量来理解
- 但理解线性变换的关键往往较少依赖特定的坐标系,更好的方法是特征向量和特征值(比如上例旋转,直接以特征向量作为旋转轴理解)
3. 特征值与特征向量计算思想 A v = λ v Av=\lambda v Av=λv — 计算 d e t ( A − λ I ) = 0 det(A-\lambda I) = 0 det(A−λI)=0求特征值
计算式子:
A A A是变换矩阵, v v v是特征向量, λ \lambda λ是一个数,为对于的特征值
- 求解 A A A矩阵特征向量与特征值,就是求解上式中 v v v与 λ \lambda λ
核心思路:
对 A v = λ v Av=\lambda v Av=λv进行变换:
所以得到: ( A − λ I ) v = 0 (A-\lambda I)v=0 (A−λI)v=0
- 如果 v v v本身就是0向量,等式成立
- 如果 v v v是非0向量的话,当且仅当矩阵代表的变换将空间压缩到更低维度时,才会存在一个非0向量,使得矩阵与它乘积为0向量(第三章第4节零空间)
而空间压缩到低纬度 对应 矩阵行列式为0
∴ \therefore ∴ 对于非0向量 v v v,为了使得 v v v经过线性变换后变成0向量,我们要找到一个 λ \lambda λ使得行列式: d e t ( A − λ I ) = 0 det(A-\lambda I) = 0 det(A−λI)=0
思路总结:
例子:对矩阵 [ 3 1 0 2 ] \left[ \begin{matrix} 3 & 1\\ 0 & 2\end{matrix} \right] [3012]进行求解特征值 λ \lambda λ和特征向量
计算 d e t ( A − λ I ) = 0 det(A-\lambda I) = 0 det(A−λI)=0
得到 λ \lambda λ后带入矩阵 A − λ I A-\lambda I A−λI中,再求解出 ( A − λ I ) v = 0 (A-\lambda I)v=0 (A−λI)v=0中的 v v v(即:求解经过变换后 成为 0向量 的向量)
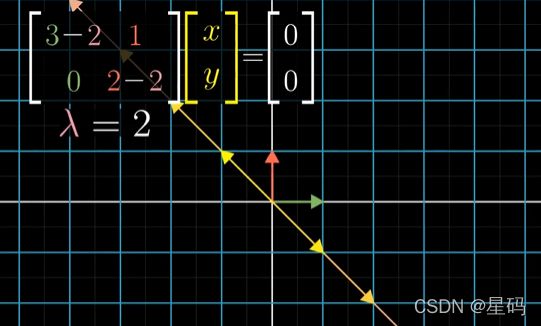
例如:求 λ = 2 \lambda=2 λ=2时对应向量
得到的所有解都落在了向量 ( − 1 , 1 ) (-1,1) (−1,1)张成的对角线上
而原始矩阵 [ 3 1 0 2 ] \left[\begin{matrix} 3 & 1\\ 0 & 2\end{matrix}\right] [3012]将这些向量拉伸为原来的2倍(因为这些向量对应特征值为2)
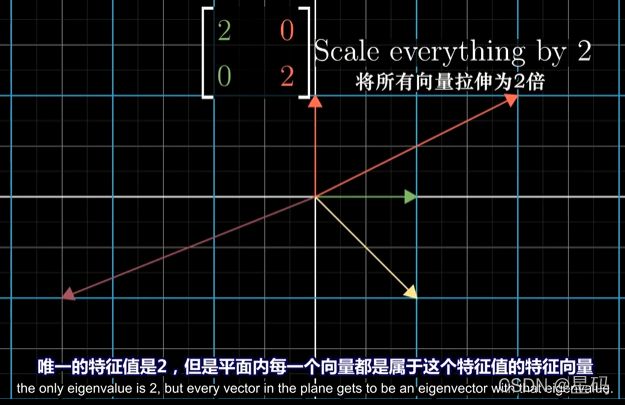
特殊情况:属于单个特征值的特征向量可以不在一条直线上(一个特征值 可以对应 多个特征向量)
4. 特征基 — 基向量都是特征向量(对角矩阵); 变换有 足以张成全空间 的特征向量集合,那么就可以变换坐标系,使得特征向量就是基向量
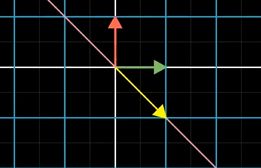
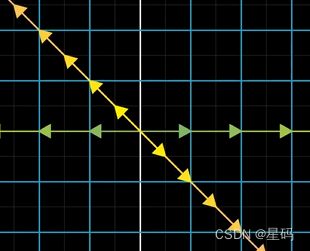
比如: i i i变成原来的 − 1 -1 −1倍, j j j变成原来的 2 2 2倍,但 i , j i,j i,j没有离开其张成的空间,会得到一个对角矩阵

如果基向量全是特征向量,对应的变换向量为:对角矩阵,对角矩阵的解读其方法是:
但基向量同时是特征向量情况比较少,但如果 变换有 足以张成全空间 的特征向量集合,那么就可以变换坐标系,使得特征向量就是基向量
第七章基变换涉及到坐标系变换:
取出想作为新基的向量坐标(在此处指的就是要作为新基的特征向量),将他们的坐标构成基变换矩阵
用特征向量作为新基意义在于:这个新矩阵必然是对角的,且对角元为对应特征值
特征向量作为新基,得到对角矩阵 的意义是:要计算非对角矩阵多次幂
- 先变换到特征基,得到一个对角矩阵
- 再在新坐标系中计算多次幂
- 最后转换回标准坐标系
九:抽象向量空间
行列式与特征向量似乎不受所选坐标系的影响,这两者都是暗含于空间中的性质
- 行列式:告诉一个变换对面积的缩放比例
- 特征向量:在变换后保留在它所张成的空间中的向量
上述提到的 空间 在之后的内容进行讲解(第3节)
0. 函数 与 向量 — 有相同可加性 和 成比例
现在讨论一种与向量有相同特性的东西 — 函数
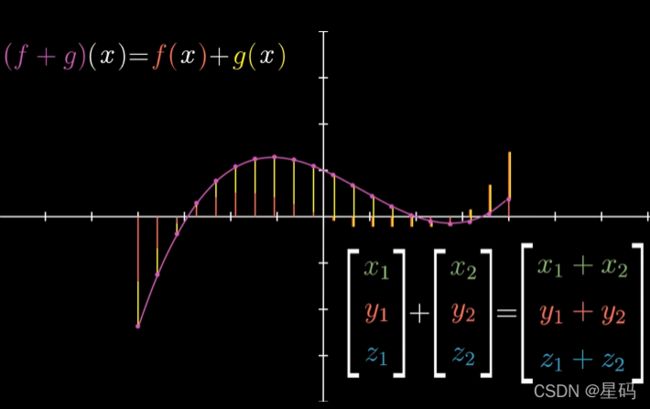
函数加法:与向量加法相似,不过从某种程度上说函数加法是无数个坐标相加
函数与实数相乘:与向量与实数相乘类似,不过是无数个坐标要相乘
∴ \therefore ∴ 最初以空间中箭头为背景考虑线性代数的合理概念和解决问题的手段,应该可以原封不动的取出来,应用于与其有类似性质的 函数
类比到函数上,例如 函数的线性变换
这个变换接受一个函数,并把它变成另一个函数(导数就是如此) — 这个概念对应着 线性算子(linear operations)
1. 线性变换的定义 — 成比例 与 可加性
一个函数变换是线性的的定义是什么?
- 可加性:将 w , v w,v w,v相加,然后对它们的和应用变换 得到的结果与 变换后的 v , w v,w v,w相加 一致
- 成比例:将 v v v与某个数相乘,然后应用变换 得到的结果与 变换后的 v v v与该数相乘 一致
即:线性变换保持加法运算和数乘运算
线性变换 — 可加性,成比例 两个性质最重要的推论:
一个线性变换可以通过他对基向量的作用来完全描述,这样使得 矩阵向量乘法成为可能
因为:任何向量都可以表达为基向量以某种方式进行的线性组合,而线性变换不改变这个线性组合(第一章第1节)
∴ \therefore ∴ 求一个向量变换后的结果 实际就是求出变换后的基向量以相同的方式进行线性组合
而后面的内容会看到: 这点对函数来说同样正确
对于函数操作的一个例子:导数
2. 用矩阵描述求导 — 矩阵向量乘法 和 函数求导 联系
为了掌握 向量,矩阵 和 函数求导 的类比关系,我们可以 使用矩阵来描述求导:
我们先规定一个空间 — 全体多项式(包含了任意高次的多项式 x 0 − > x 高 次 x^0 -> x^{高次} x0−>x高次)
想要把多项式当作向量来处理:
先赋予这个空间坐标的含义 — 即规定空间的基:因为多项式就是 x x x的不同次幂数乘再加和,所以,选取 x x x的不同次幂作为基函数
用矩阵描述函数求导:
使用求导矩阵进行求导:( x 3 + 5 x 2 + 4 x + 5 x^3+5x^2+4x+5 x3+5x2+4x+5)
先将这个多项式化成向量,在使用矩阵向量乘法得到结果
**正是因为上述中 求导满足线性性质(本章第1节),使得这个过程称为可能**
3. 向量空间与公理 — 如果满足公理,就可以在其他奇怪的向量空间中使用已有结论
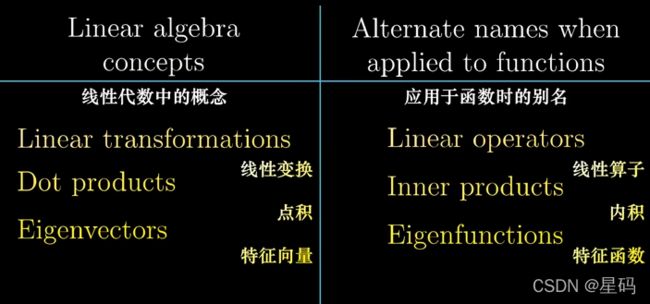
这就使得矩阵向量乘法 和 矩阵求导 进行了联系,而其实有很多概念都可以进行类比:
数学中有很多类似事物可以与向量类比:只要处理的对象集有合理的数乘和相加的概念,那么线性代数中所有关于向量,线性变换以及其他概念都适用于它
向量空间
- 这些类似向量的事物,比如:箭头;一组数;函数等,他们构成的集合称为“向量空间” (之前的例子中,函数构成集合就是一种向量空间)
- 向量空间中 有一系列向量加法和数乘必须遵守的规则 — 公理
而在线性代数现代理论中,如果让所有已经建立好的理论和概念适用于一个向量空间,其必须满足八条公理:

这样就可以保证向量加法与数乘的概念确实如所想那样 - 如果满足公理,就可以在其他奇怪的向量空间中使用已有结论 — 比如函数满足线性代数8条公理,那么线性代数中的结论都可以运用到函数上
补1:克莱姆法则几何解释 — 变换后向量与变换后基向量构成的面积(体积) 与 变化之前的比例 可以用 变换矩阵的行列式衡量
[ − 4 2 3 − 1 0 2 − 4 6 − 9 ] [ x y z ] = [ 7 − 8 3 ] \left[\begin{matrix} -4 & 2 & 3\\ -1 & 0 & 2 \\ -4 & 6 & -9 \\ \end{matrix}\right] \left[\begin{matrix} x\\ y \\ z \\ \end{matrix}\right] = \left[\begin{matrix} 7\\ -8 \\ 3 \\ \end{matrix}\right] ⎣⎡−4−1−420632−9⎦⎤⎣⎡xyz⎦⎤=⎣⎡7−83⎦⎤
背景知识:(在上一篇博客中:点击此处)
不过:克莱姆法则不是解线性方程组最好的方法,高斯消元法会更快,但理解克莱姆法则会更加理解线性代数
只要未知数和方程个数相同,一般都可以使用克莱姆法则,一个例子:
方程组可以看成对 ( x , y ) (x,y) (x,y)向量的一个已知矩阵变换
- ( x , y ) (x,y) (x,y)其变换结果是 ( − 4 , − 2 ) (-4,-2) (−4,−2)
- 而矩阵说明了是如何变换的,其列表明变换后基向量的位置
然而:当矩阵行列式为0时 ( d e t ( A ) = 0 ) (det(A)=0) (det(A)=0),即:变换之后降了维(例如:二维空间压缩成一条线 — 第二章第4节)
以下只讨论非0行列式的情况,即线性变换后维数依然相同
对于非0行列式情况:
构建与向量每个坐标有关的面积 — 使用行列式来构建(第二章第4节)
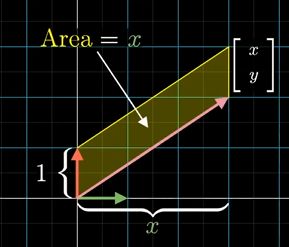
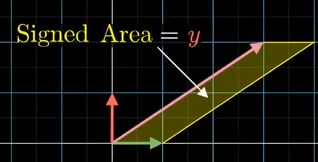
第一个基向量 i i i和未知向量 ( x , y ) (x,y) (x,y)构成平行四边形面积来表示 y y y
第二个基向量 j j j和未知向量 ( x , y ) (x,y) (x,y)构成平行四边形的面积来表示 x x x
表示三维中的 z z z时,用向量与基向量 i , j i,j i,j 所组成的平行六面体 的体积(底面为1,高为 z z z)
同样的,对于三维,可以用:
- x = d e t ( [ x 0 0 y 1 0 z 0 1 ] ) x = det(\left[\begin{matrix} x & 0 & 0\\ y & 1 & 0 \\ z & 0 & 1 \\ \end{matrix}\right]) x=det(⎣⎡xyz010001⎦⎤),
- y = d e t ( [ 1 x 0 0 y 0 0 z 1 ] ) y = det(\left[\begin{matrix} 1 & x & 0\\ 0 & y & 0 \\ 0 & z & 1 \\ \end{matrix}\right]) y=det(⎣⎡100xyz001⎦⎤)
- 这个方法可以描述一个向量的某一坐标轴上位置 — 和除这个坐标轴之外的其他轴组成平行六面体,其体积就是对应的坐标轴
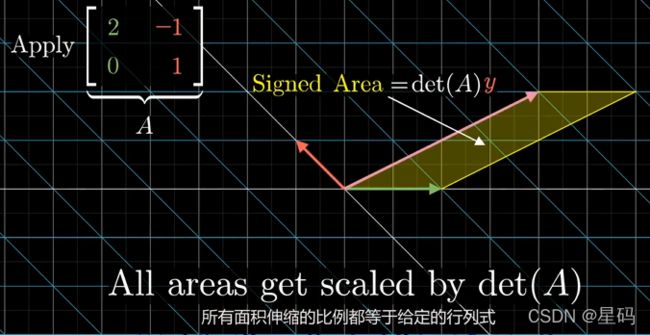
之所以使用行列式,是因为:变换前后所有面积伸缩比例都是一样的,而变换矩阵的行列式可以描述这个比例(第二章第4节)
变换前:向量与基向量 i i i构成的面积
变换后:向量经过了矩阵 A A A的变换,成了 A x Ax Ax,基向量也发生了变换
但是 变换后向量与变换后基向量 i i i构成的面积 与 之前面积比例 可以用 变换矩阵的行列式衡量
∴ \therefore ∴ 可以得到 y y y的式子为:
接下来求解 变换后向量与变换后基向量 i i i构成的面积(Area) 就可以得到 y y y
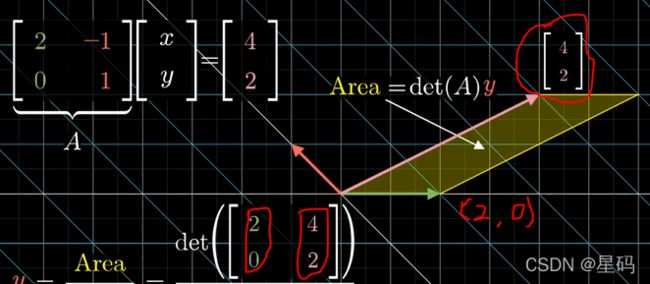
对于一个线性方程组: 2 x − 1 y = 4 2x-1y=4 2x−1y=4; 0 x + 1 = 2 0x+1=2 0x+1=2
变成矩阵向量形式为: [ 2 − 1 0 1 ] [ x y ] = [ 4 2 ] \left[\begin{matrix} 2 & -1 \\ 0 & 1\end{matrix}\right] \left[\begin{matrix} x\\ y \\ \end{matrix}\right] = \left[\begin{matrix} 4\\ 2 \\ \end{matrix}\right] [20−11][xy]=[42]
可以得到这个向量变换后的向量 — 变换后,向量 ( x , y ) (x,y) (x,y)变成了 ( 4 , 2 ) (4,2) (4,2)
∴ \therefore ∴ 变换后向量与变换后基向量 i i i构成的面积 — 就可以用一个行列式来表述:行列式中第一列为变换后的 i i i,第二列为变换后的向量
综上,得到了原来向量的坐标 y y y:

同理可以解 x x x:

补2:计算二阶矩阵特征值的妙计 — 与韦达定理联系
参考视频:计算二阶矩阵特征值的妙计
回顾:第八章特征值与特征向量
某个向量,进行线性变换后,其仍留在向量张成的空间中(即:只是缩放了若干倍),这个向量就是 特征向量,特征向量缩放的倍数就是相应的 特征值
即转化成式子: A v = λ v Av=\lambda v Av=λv对式子进行转化: ( A − λ I ) v = 0 (A-\lambda I)v=0 (A−λI)v=0
这意味着:
- 变换矩阵 ( A − λ I ) (A-\lambda I) (A−λI) 将 A对应非0特征向量 变换为0向量
- ( A − λ I ) (A-\lambda I) (A−λI)这个矩阵其行列式为0
求解特征值时:利用性质 — d e t ( A − λ I ) = 0 det(A-\lambda I)=0 det(A−λI)=0
这个求解过程比较复杂,对二阶矩阵来说,有种更直接的方法
计算二阶矩阵特征值的妙计
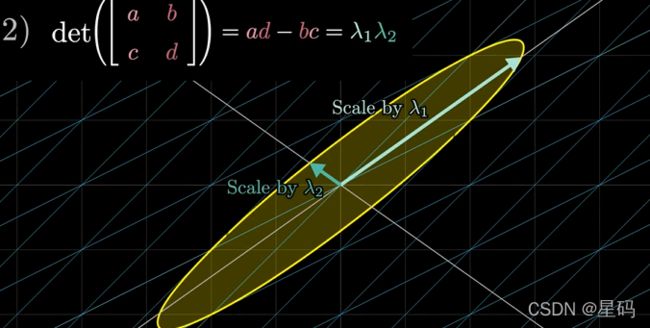
对矩阵 [ a b c d ] \left[\begin{matrix} a & b \\ c & d\end{matrix}\right] [acbd]
- 矩阵的“迹”(就是主对角元总和) = = = 矩阵各特征值的总和
∴ \therefore ∴ 两特征值的平均数等于两个主对角元的平均数- 二阶矩阵的行列式(即: a d − b c ad-bc ad−bc) = = = 两个特征值的乘积
- λ 1 , λ 2 = m ± m 2 − p \lambda_1,\lambda_2=m\plusmn\sqrt{m^2-p} λ1,λ2=m±m2−p
定义 m = ( a + b ) / 2 = ( λ 1 + λ 2 ) / 2 m=(a+b)/2=(\lambda_1+\lambda_2)/2 m=(a+b)/2=(λ1+λ2)/2; p = a d − b c = λ 1 λ 2 p=ad-bc=\lambda_1\lambda_2 p=ad−bc=λ1λ2
有一个二阶矩阵,就有 a , b , c , d a,b,c,d a,b,c,d,也就求出 m , p m,p m,p,接下来求特征值
两个特征值均值为 m m m,设这两个特征值到 m m m的距离为 d d d
即: λ 1 = m − d , λ 2 = m + d \lambda_1=m-d,\lambda_2=m+d λ1=m−d,λ2=m+d
∴ \therefore ∴ λ 1 λ 2 = ( m − d ) ( m + d ) = m 2 − d 2 = p \lambda_1\lambda_2=(m-d)(m+d)=m^2-d^2=p λ1λ2=(m−d)(m+d)=m2−d2=p
得到了 d = m 2 − p d=\sqrt{m^2-p} d=m2−p
∴ \therefore ∴ λ 1 , λ 2 = m ± m 2 − p \lambda_1,\lambda_2=m\plusmn\sqrt{m^2-p} λ1,λ2=m±m2−p
记忆顺口溜
解二次方程的通用方法 — 韦达定理
对于我们计算二阶矩阵特征值( λ 1 , λ 2 \lambda_1,\lambda_2 λ1,λ2)
利用 d e t ( A − λ I ) = 0 det(A-\lambda I)=0 det(A−λI)=0,化解后是一个一元二次方程(两个特征值为方程的解)
∴ \therefore ∴ 这个方程可以写为 ( x − λ 1 ) ( x − λ 2 ) = x 2 − ( λ 1 + λ 2 ) x + λ 1 λ 2 (x-\lambda_1)(x-\lambda_2)=x^2-(\lambda_1+\lambda_2)x+\lambda_1\lambda_2 (x−λ1)(x−λ2)=x2−(λ1+λ2)x+λ1λ2
而韦达定理中求解 ( − b ± b 2 − 4 a c ) / ( 2 a ) (-b\plusmn\sqrt{b^2-4ac})/(2a) (−b±b2−4ac)/(2a)
对计算二阶矩阵特征值的方程使用韦达定理: a = 1 , b = λ 1 + λ 2 = 2 m , c = λ 1 λ 2 = p a=1,b=\lambda_1+\lambda_2=2m,c=\lambda_1\lambda_2=p a=1,b=λ1+λ2=2m,c=λ1λ2=p
将其带入韦达定理公式,则得到 m ± m 2 − p m\plusmn\sqrt{m^2-p} m±m2−p

也即:使用特征值的和,积与矩阵元素的关系求特征值 与 直接对 二阶矩阵特征值的方程( d e t ( A − λ I ) = 0 det(A-\lambda I)=0 det(A−λI)=0) 使用韦达定理求解 得到的结果相同
且我们赋予了结果中 m , p m,p m,p的含义( m = ( a + b ) / 2 = ( λ 1 + λ 2 ) / 2 m=(a+b)/2=(\lambda_1+\lambda_2)/2 m=(a+b)/2=(λ1+λ2)/2; p = a d − b c = λ 1 λ 2 p=ad-bc=\lambda_1\lambda_2 p=ad−bc=λ1λ2)
参考视频
【官方双语/合集】线性代数的本质 - 系列合集:https://www.bilibili.com/video/BV1ys411472E?p=1
【官方双语】计算二阶矩阵特征值的妙计 – 线性代数的本质 13:https://www.bilibili.com/video/BV12K4y1A7NA?spm_id_from=333.999.0.0
原能在运用直观思维时找到乐趣,同时也祝在今后学习中顺利
(So, have fun applying those intuitions and best of luck with future learning.)