【计算机视觉|生成对抗】非配对图像到图像的翻译：使用循环一致对抗网络（CycleGAN）

本系列博文为深度学习/计算机视觉论文笔记，转载请注明出处

标题：Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks

链接：[1703.10593] Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks (arxiv.org)

摘要

图像到图像的转换是一类涉及视觉和图形问题的任务，其目标是通过一组配准的图像对训练集来学习将输入图像映射到输出图像。然而，在许多任务中，很难获得配对的训练数据。我们提出了一种方法，用于在没有配对样本的情况下学习从源领域 $X$ 到目标领域 $Y$ 的图像转换。我们的目标是学习一个映射 $G:X\to Y$，使得从 $G(X)$ 产生的图像分布在使用对抗性损失时与领域 Y 的分布不可区分。由于这种映射存在很大的不确定性，因此我们引入了一个逆映射 $F:Y\to X$，并引入循环一致性损失来强制执行 $F(G(X))\approx X$（反之亦然）。我们在多个任务中展示了没有配对训练数据的定性结果，包括风格转换、物体变形、季节转换、照片增强等。通过与几种先前方法进行定量比较，证明了我们方法的优越性。

1. 引言

克劳德·莫奈在1873年一个美丽的春日，在塞纳河畔阿让特伊堡附近放置他的画架时，他看到了什么景象呢？如果彩色摄影术已经发明，或许可以记录下清澈的蓝天和倒映其中的玻璃般的河水。然而，莫奈通过轻柔的笔触和鲜艳的调色表达了他对同一场景的印象。

如果莫奈在凉爽的夏日傍晚来到卡西斯的小港口，会是怎样的景象呢？透过一系列莫奈的画作，我们可以想象他如何描绘这个场景：或许使用柔和的色调，粗糙的颜料涂抹和较为平坦的动态范围。

尽管我们从未见过莫奈的画作与所画场景的照片并排放置，但我们了解莫奈画作的集合和风景照片的集合。我们可以推理出这两个集合之间的风格差异，从而想象出将一个场景从一个集合“转换”到另一个集合会是什么样子。

在本文中，我们提出了一种可以实现类似效果的方法：捕捉一个图像集合的特殊特征，并找出如何将这些特征转换到另一个图像集合中，所有这些都在没有任何配对的训练示例的情况下进行。

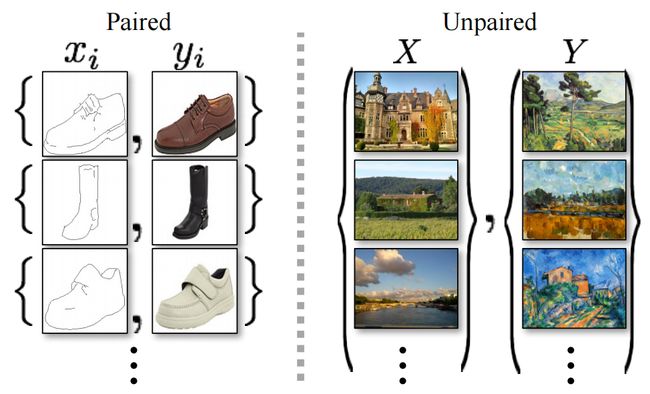
这个问题可以更广泛地描述为图像到图像的转换，将一个给定场景的表示，$x$，转换为另一个表示，$y$，例如，从灰度到彩色、从图像到语义标签、从边缘图到照片。多年来，在监督设置下，计算机视觉、图像处理、计算摄影和图形学领域的研究已经产生了强大的翻译系统，其中可以获得示例图像对$\{x_i,y_i{\}}_{i=1}^N$ （图2，左），例如[11, 19, 22, 23, 28, 33, 45, 56, 58, 62]。然而，获得配对的训练数据可能会很困难和昂贵。例如，对于语义分割等任务，只有少数几个数据集存在（例如[4]），而且它们相对较小。对于艺术风格化等图形任务获得输入-输出对甚至更加困难，因为所需的输出非常复杂，通常需要艺术创作。对于许多任务，如物体变形（例如斑马↔马，图1中上方），期望的输出甚至没有明确定义。

图1： 给定任意两组无序的图像集合X和Y，我们的算法学会自动地在这两组图像之间进行“翻译”，将一组图像转化为另一组，反之亦然：（左）来自Flickr的莫奈绘画和风景照片；（中）来自ImageNet的斑马和马；（右）来自Flickr的夏季和冬季优胜美地照片。示例应用（底部）：通过一系列著名艺术家的绘画作品，我们的方法学会将自然照片渲染成相应的艺术风格。

图2： 配对训练数据（左侧）包括训练示例 {$x_i,y_i$}，其中$x_i$与$y_i$之间存在对应关系[22]。相反，我们考虑了不配对的训练数据（右侧），由源集合 {$x_i$}（$x_i\in X$）和目标集合 {$y_j$}（$y_j\in Y$）组成，但没有提供哪个$x_i$与哪个$y_j$相对应的信息。

因此，我们寻求一种算法，可以在没有配对的输入-输出示例的情况下学习在领域之间进行转换（图2，右）。我们假设领域之间存在某种基本关系——例如，它们是同一基础场景的两种不同呈现方式——并试图学习该关系。虽然我们缺乏配对示例形式的监督，但我们可以在集合级别上利用监督：我们在领域$X$中给定一组图像，以及在领域$Y$中给定另一组图像。我们可以训练一个映射$G:X\to Y$，使得输出$y^{\prime }=G(x)$，其中$x\in X$，通过一个对抗性分类器训练来使其与领域$Y$中的图像$y\in Y$难以区分。在理论上，这个目标可以引出一个关于$y^{\prime }$的输出分布，该分布与经验分布$p_{\text{data}}(y)$相匹配（一般来说，这需要$G$是随机的）[16]。这样，最优的$G$将领域$X$转换为与$Y$的分布完全相同的领域$Y^{\prime }$。

然而，这样的转换并不保证一个个体输入$x$和输出$y$在有意义的方式上成对匹配——存在无限多个映射$G$，会导致相同的$y^{\prime }$分布。此外，实际上，我们发现难以单独优化对抗性目标：标准程序常常导致众所周知的模式坍塌问题，其中所有输入图像映射到同一输出图像，优化无法取得进展。

这些问题要求我们为目标添加更多的结构。因此，我们利用了翻译应该是“循环一致”的属性，即如果我们将一个句子从英语翻译成法语，然后再从法语翻译回英语，我们应该回到原始句子。从数学上讲，如果我们有一个翻译器$G:X\to Y$和另一个翻译器$F:Y\to X$，则$G$和$F$应该是彼此的逆映射，而且两个映射都应该是双射。我们通过同时训练映射$G$和$F$，并添加循环一致性损失[64]，鼓励$F(G(x))\approx x$和$G(F(y))\approx y$。将这个损失与领域$X$和$Y$上的对抗性损失相结合，就得到我们用于非配对图像到图像转换的完整目标。

我们将我们的方法应用于广泛的应用，包括集合风格转换、物体变形、季节转换和照片增强。我们还与先前的方法进行比较，这些方法要么依赖于手动定义的风格和内容分解，要么依赖于共享的嵌入函数，并展示出我们的方法优于这些基准。我们提供了PyTorch和Torch的实现。在我们的网站上查看更多结果。

2. 相关工作

生成对抗网络（GANs）[16, 63] 在图像生成 [6, 39]、图像编辑 [66] 和表示学习 [39, 43, 37] 方面取得了令人印象深刻的成果。近期的方法将相同的思想应用于条件图像生成应用，例如文本到图像 [41]、图像修复 [38] 和未来预测 [36]，以及其他领域，如视频 [54] 和3D数据 [57]。GAN的成功关键在于对抗性损失的思想，该损失迫使生成的图像在原则上与真实照片无法区分。这个损失对图像生成任务尤其有效，因为这正是计算机图形学的许多目标所要优化的。我们采用对抗性损失来学习映射，使得转换后的图像与目标领域中的图像无法区分。

图像到图像的转换 图像到图像转换的思想至少可以追溯到Hertzmann等人的“图像类比”[19]，他们在单个输入-输出训练图像对上使用了非参数纹理模型[10]。更近期的方法使用输入-输出示例数据集，使用CNN学习参数化的翻译函数（例如[33]）。我们的方法建立在Isola等人的“pix2pix”框架[22]之上，该框架使用条件生成对抗网络[16]来学习从输入到输出图像的映射。类似的思想已经应用于各种任务，如从草图生成照片[44]或从属性和语义布局生成照片[25]。然而，与上述先前的工作不同，我们在没有配对训练示例的情况下学习映射。

无配对图像到图像转换 其他一些方法也处理无配对设置，其中目标是关联两个数据领域：X 和 Y。Rosales等人[42]提出了一个贝叶斯框架，其中包括基于源图像计算的基于块的马尔科夫随机场先验和从多个样式图像获得的似然项。最近，CoGAN [32] 和交叉模态场景网络 [1] 使用权重共享策略在领域之间学习共同表示。与我们的方法同时进行的Liu等人[31]在上述框架中加入变分自动编码器[27]和生成对抗网络[16]的组合。并行工作线 [46, 49, 2] 鼓励输入和输出在特定的“内容”特征上共享，即使它们在“风格”上可能有所不同。这些方法也使用对抗网络，附加项强制输出在预定义的度量空间中接近输入，例如类别标签空间 [2]、图像像素空间 [46] 和图像特征空间 [49]。

与上述方法不同，我们的表述不依赖于任务特定的、预定义的输入和输出之间的相似性函数，也不假设输入和输出必须位于相同的低维嵌入空间中。这使得我们的方法成为许多视觉和图形任务的通用解决方案。我们在第5.1节直接与几种先前和同时期的方法进行了比较。

循环一致性 使用传递性作为规范化结构化数据的方法有着悠久的历史。在视觉跟踪中，强制简单的前向-后向一致性已经是几十年来的标准技巧 [24, 48]。在语言领域，通过“回译和协调”来验证和改进翻译是人类翻译员[3]（包括幽默地，马克·吐温[51]）以及机器[17]使用的技术。最近，在运动结构 [61]、3D形状匹配 [21]、共分割 [55]、密集语义对齐 [65, 64] 和深度估计 [14] 方面，更高阶的循环一致性已被使用。其中，Zhou等人[64]和Godard等人[14]最接近我们的工作，因为他们使用循环一致性损失作为使用传递性监督CNN训练的一种方式。在这项工作中，我们引入了类似的损失，以使$G$和$F$彼此一致。与我们的工作同时进行的是，在这些相同的会议中，Yi等人[59]独立地使用了类似的目标进行无配对图像到图像的转换，受到了机器翻译中的双向学习的启发。

神经风格转移 神经风格转移[13, 23, 52, 12] 是进行图像到图像转换的另一种方法，它通过将一个图像的内容与另一个图像的风格（通常是绘画）结合起来，基于匹配预训练深度特征的格拉姆矩阵统计信息。与之相反，我们的主要关注点是学习两个图像集合之间的映射，而不是两个特定图像之间的映射，试图捕捉更高级的外观结构之间的对应关系。因此，我们的方法可以应用于其他任务，如绘画→照片、物体变形等，这些任务单一样本转换方法无法很好地执行。我们在第5.2节比较了这两种方法。

3. 公式化

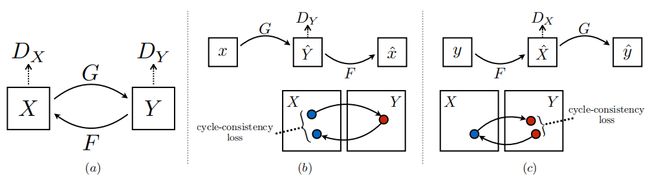
我们的目标是在给定训练样本 $\{x_i{\}}_{i=1}^N$，其中 $x_i\in X$，和 $\{y_j{\}}_{j=1}^M$，其中 $y_j\in Y$ ¹的情况下，学习两个领域 $X$ 和 $Y$ 之间的映射函数。我们将数据分布表示为 $x\sim p_{\text{data}}(x)$ 和 $y\sim p_{\text{data}}(y)$。如图3(a)所示，我们的模型包括两个映射 $G:X\to Y$ 和 $F:Y\to X$。此外，我们引入两个对抗性鉴别器 $D_X$ 和 $D_Y$，其中 $D_X$ 旨在区分图像 $\{x\}$ 和翻译后的图像 $\{F(y)\}$，同样地，$D_Y$ 旨在区分 $\{y\}$ 和 $\{G(x)\}$。我们的目标包含两种类型的项：对抗性损失 [16] 用于使生成的图像分布与目标领域中的数据分布匹配；循环一致性损失用于防止学习到的映射 $G$ 和 $F$ 相互矛盾。

图3： (a) 我们的模型包含两个映射函数 $G:X\to Y$ 和 $F:Y\to X$，以及相关的对抗性判别器 $D_Y$ 和 $D_X$。 $D_Y$ 促使 $G$ 将 $X$ 转换为与领域 $Y$ 中的输出无法区分的结果，对于 $D_X$ 和 $F$ 也是如此。为了进一步规范这些映射，我们引入了两个循环一致性损失，捕捉到的直觉是，如果我们从一个领域翻译到另一个领域，然后再次返回，我们应该回到起点：(b) 前向循环一致性损失：$x\to G(x)\to F(G(x))\approx x$，以及 © 反向循环一致性损失：$y\to F(y)\to G(F(y))\approx y$。

3.1. 对抗性损失

我们对两个映射函数都应用对抗性损失 [16]。对于映射函数 $G:X\to Y$ 及其鉴别器 $D_Y$，我们表达目标为：

$$L_{\text{GAN}}(G,D_Y,X,Y)=E_{y\sim p_{\text{data}}(y)}[\log D_Y(y)]+E_{x\sim p_{\text{data}}(x)}[\log (1-D_Y(G(x)))]\text{\hspace{1em}(1)}$$

其中 $G$ 试图生成类似于来自领域 $Y$ 的图像 $G(x)$，而 $D_Y$ 旨在区分翻译样本 $G(x)$ 和真实样本 $y$。$G$ 旨在最小化这个目标，而对手 $D$ 则试图将其最大化，即：

$$\underset{G}{\min }\underset{D_Y}{\max }{L}_{\text{GAN}}(G,D_Y,X,Y)$$

我们也为映射函数 $F:Y\to X$ 及其鉴别器 $D_X$ 引入类似的对抗性损失：

$$\underset{F}{\min }\underset{D_X}{\max }{L}_{\text{GAN}}(F,D_X,Y,X)$$

3.2. 循环一致性损失

理论上，对抗性训练可以学习映射 $G$ 和 $F$，使其输出在目标领域 $Y$ 和 $X$ 中分布完全相同（严格来说，这要求 $G$ 和 $F$ 是随机函数）[15]。然而，使用足够大的容量，网络可以将同一组输入图像映射到目标领域中的任何随机排列图像，任何学习到的映射都可以引导输出分布与目标分布相匹配。因此，仅仅通过对抗性损失无法保证学习到的函数能够将单个输入 $x_i$ 映射到期望的输出 $y_i$。为了进一步减少可能映射函数的空间，我们认为学习到的映射函数应当具备循环一致性：如图3(b)所示，对于每个来自领域 $X$ 的图像 $x$，图像转换循环应当能够将 $x$ 带回原始图像，即 $x\to G(x)\to F(G(x))\approx x$。我们将其称为前向循环一致性。类似地，如图3©所示，对于每个来自领域 $Y$ 的图像 $y$，$G$ 和 $F$ 也应满足反向循环一致性：$y\to F(y)\to G(F(y))\approx y$。我们使用循环一致性损失来激励这种行为：

$$L_{\text{cyc}}(G,F)=E_{x\sim p_{\text{data}}(x)}[\Vert F(G(x))-x{\Vert }_1]+E_{y\sim p_{\text{data}}(y)}[\Vert G(F(y))-y{\Vert }_1]\text{\hspace{1em}(2)}$$

在初步实验中，我们还尝试了将此损失中的 L1 范数替换为 $F(G(x))$ 和 $x$ 之间的对抗性损失，以及 $G(F(y))$ 和 $y$ 之间的对抗性损失，但没有观察到性能改善。

循环一致性损失引发的行为可以在图4中观察到：重构图像 $F(G(x))$ 最终与输入图像 $x$ 非常相似。

图4： 输入图像 $x$，输出图像 $G(x)$ 和从各种实验中重构的图像 $F(G(x))$。从上到下分别是：照片↔塞尚风格，马↔斑马，冬季→夏季优胜美地，航拍照片↔谷歌地图。

3.3. 完整目标

我们的完整目标为：

$$L(G,F,D_X,D_Y)=L_{\text{GAN}}(G,D_Y,X,Y)+L_{\text{GAN}}(F,D_X,Y,X)+\lambda L_{\text{cyc}}(G,F)\text{\hspace{1em}(3)}$$

其中 $\lambda$ 控制了两个目标的相对重要性。我们的目标是解决：

$$G^{\ast },F^{\ast }=\arg \underset{G,F}{\min }\underset{D_X,D_Y}{\max }L(G,F,D_X,D_Y)$$

需要注意的是，我们的模型可以被视为训练了两个“自动编码器”[20]：我们共同学习一个自动编码器 $F\circ G:X\to X$ 以及另一个 $G\circ F:Y\to Y$。然而，这些自动编码器每个都具有特殊的内部结构：它们通过将图像转换为另一个领域中的翻译来将图像映射到自身。这样的设置也可以被视为“对抗性自动编码器”的特殊情况[34]，该自动编码器使用对抗性损失来训练自动编码器的瓶颈层，以匹配任意的目标分布。在我们的情况下，$X\to X$ 自动编码器的目标分布是领域 $Y$ 的分布。

在第5.1.4节中，我们将我们的方法与仅使用对抗性损失 $L_{\text{GAN}}$ 或仅使用循环一致性损失 $L_{\text{cyc}}$ 的消融结果进行比较，并经验性地表明两个目标在实现高质量结果方面起到了关键作用。我们还在单向循环损失的情况下进行了评估，表明单个循环不足以规范这个不受约束的问题的训练。

4. 实现

网络架构 我们采用了 Johnson 等人的网络架构 [23]，他们在神经风格迁移和超分辨率方面取得了令人印象深刻的结果。这个网络包含三个卷积层，若干残差块 [18]，两个步长为 1/2 的分数卷积层，以及一个将特征映射到 RGB 的卷积层。对于 128 × 128 的图像，我们使用 6 个块，对于 256 × 256 及更高分辨率的训练图像，我们使用 9 个块。类似于 Johnson 等人 [23]，我们使用了实例归一化 [53]。对于鉴别器网络，我们使用了 70 × 70 的 PatchGANs [22, 30, 29]，其目标是对 70 × 70 的重叠图像块进行分类，判断它们是真实还是伪造的。这种基于块级别的鉴别器架构的参数比全图鉴别器少，可以在完全卷积的方式下处理任意大小的图像 [22]。

训练细节 我们采用了近期工作中的两种技术来稳定模型训练过程。首先，在 LGAN（公式 1）中，我们将负对数似然目标替换为最小二乘损失 [35]。这个损失在训练过程中更加稳定，生成了更高质量的结果。特别地，对于 GAN 损失 LGAN(G, D, X, Y)，我们训练 G 以最小化 $E_{x\sim p_{\text{data}}(x)}[(D(G(x))-1{)}^2]$，训练 D 以最小化 $E_{y\sim p_{\text{data}}(y)}[(D(y)-1{)}^2]+E_{x\sim p_{\text{data}}(x)}[D(G(x){)}^2]$。

其次，为了减少模型震荡 [15]，我们遵循 Shrivastava 等人的策略 [46]，使用历史生成图像来更新鉴别器，而不是最新生成器产生的图像。我们保持一个图像缓冲区，存储最近创建的 50 张图像。

对于所有实验，我们将公式 3 中的 $\lambda$ 设置为 10。我们使用 Adam 优化器 [26]，批大小为 1。所有网络都从头开始训练，学习率为 0.0002。我们在前 100 个 epoch 使用相同的学习率，然后在接下来的 100 个 epoch 线性减少学习率至零。更多关于数据集、架构和训练过程的细节，请参见附录（第 7 节）。

5. 结果

我们首先在具有配对数据集的情况下将我们的方法与最近的无配对图像到图像翻译方法进行比较，其中存在用于评估的真实输入-输出配对数据。然后，我们研究了对抗性损失和循环一致性损失的重要性，并将我们的完整方法与几个变体进行比较。最后，我们在没有配对数据的广泛应用领域展示了我们算法的普适性。为了简洁起见，我们将我们的方法称为 CycleGAN。PyTorch 和 Torch 的代码、模型和完整的结果可以在我们的网站上找到。

5.1 评估

使用与“pix2pix” [22] 相同的评估数据集和指标，我们从定性和定量两方面对比了我们的方法与几种基准方法。任务包括在 Cityscapes 数据集上的语义标签↔照片，以及从谷歌地图中抓取的地图↔航拍照片。我们还对完整损失函数进行了消融研究。

5.1.1 评估指标

AMT 感知研究 对于地图↔航拍照片任务，我们在 Amazon Mechanical Turk（AMT）上进行了“真实 vs 伪造”感知研究，以评估我们输出的真实性。我们遵循了 Isola 等人 [22] 的感知研究协议，只是我们每个测试的算法只收集了 25 名参与者的数据。参与者将看到一系列的图像对，一个是真实照片或地图，另一个是伪造的（由我们的算法或基准方法生成），然后被要求点击他们认为是真实的图像。每个会话的前 10 个试验是练习，会给出参与者的回应是正确还是错误。其余的 40 个试验被用来评估每个算法欺骗参与者的比率。每个会话只测试一个算法，参与者只允许完成一个会话。我们报告的数据与 [22] 中的数据不直接可比²，因为我们的基准图像经过了轻微的处理，并且我们测试的参与者群体可能与 [22] 中的参与者群体有所不同（由于在不同的日期和时间运行实验）。因此，我们的数据只应该用来将我们当前的方法与基准方法进行比较（在相同的条件下运行基准方法），而不是与 [22] 进行比较。

FCN 分数 尽管感知研究可能是评估图形真实性的黄金标准，但我们还希望有一种不需要人类实验的自动定量衡量方法。为此，我们采用了 [22] 中的“FCN 分数”，并将其用于评估 Cityscapes 标签→照片任务。FCN 指标评估了生成的照片在外部预训练的语义分割算法（来自 [33] 的完全卷积网络 FCN）下的可解释性。FCN 预测了生成照片的标签映射。然后，可以将这个标签映射与输入的地面真实标签进行比较，使用下面描述的标准语义分割指标。其核心思想是，如果我们从一个“道路上的汽车”标签映射生成一张照片，那么当应用于生成的照片时，FCN 应该检测出“道路上的汽车”。

语义分割指标 为了评估照片→标签任务的性能，我们使用了 Cityscapes 基准数据集 [4] 中的标准指标，包括每像素精度、每类精度和平均类别交并比（Class IOU） [4]。

5.1.2 基准方法

CoGAN [32] 该方法学习一个用于域 X 的 GAN 生成器和一个用于域 Y 的生成器，其中前几层的权重是相同的，用于共享的潜在表示。从 X 到 Y 的转换可以通过找到一个能够生成图像 X 的潜在表示，然后将该潜在表示渲染到风格 Y 中来实现。

SimGAN [46] 类似于我们的方法，Shrivastava 等人 [46] 使用对抗性损失来训练从 X 到 Y 的转换。正则化项 $kx-G(x)k_1$ 用于惩罚在像素级别上进行大幅度的变化。

特征损失 + GAN 我们还测试了 SimGAN [46] 的一个变体，其中 L1 损失是在预训练网络（VGG-16 relu4 2 [47]）的深层图像特征上计算的，而不是在 RGB 像素值上计算的。在深度特征空间中计算距离，有时也被称为“感知损失” [8, 23]。

BiGAN/ALI [9, 7] 无条件 GAN [16] 学习一个生成器 G: Z → X，将随机噪声 z 映射到图像 x。BiGAN [9] 和 ALI [7] 提出还要学习逆映射函数 F: X → Z。虽然它们最初是设计用于将潜在向量 z 映射到图像 x，但我们实现了相同的目标，将源图像 x 映射到目标图像 y。

pix2pix [22] 我们还将我们的结果与 pix2pix [22] 进行了比较，后者在配对数据上进行训练，以查看在没有使用任何配对数据的情况下，我们能够接近这个“上限”。为了公平比较，我们使用与我们的方法相同的架构和细节，除了 CoGAN [32]。CoGAN 基于生成器，该生成器根据共享的潜在表示生成图像，这与我们的图像到图像网络不兼容。我们使用 CoGAN 的公开实现。

5.1.3 与基准方法的比较

如图5和图6所示，我们无法使用任何基准方法获得令人信服的结果。然而，我们的方法可以生成与完全监督的 pix2pix 相似质量的转换。

图5： 在Cityscapes图像上训练的不同标签↔照片映射方法。从左到右：输入图像，BiGAN/ALI [7, 9]，CoGAN [32]，特征损失 + GAN，SimGAN [46]，CycleGAN（我们的方法），pix2pix [22]（基于配对数据训练），以及真实地面实况图像。

图6： 不同方法在Google Maps上训练的航拍照片↔地图映射。从左到右：输入，BiGAN/ALI [7, 9]，CoGAN [32]，特征损失 + GAN，SimGAN [46]，CycleGAN（我们的方法），pix2pix [22]（基于配对数据训练），和真实地面实况。

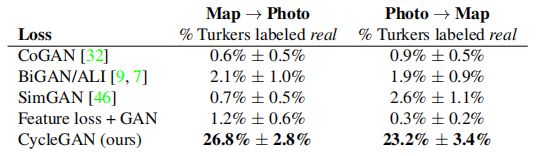
表1报告了与AMT感知逼真性任务相关的性能。在这里，我们可以看到在256×256的分辨率下，我们的方法在地图→航拍照片方向和航拍照片→地图方向上都能在约四分之一的试验中欺骗参与者³。所有的基线方法几乎从未欺骗过参与者。

表1： 在256×256分辨率下对地图↔航拍照片进行的AMT“真实 vs 假的”测试。

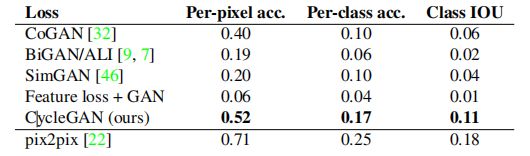
表2评估了Cityscapes数据集上的标签→照片任务的性能，而表3则评估了相反的映射（照片→标签）。在这两种情况下，我们的方法再次超越了基线方法。

表2： 不同方法的FCN分数，在Cityscapes数据集上对标签→照片进行评估。

表3： 在Cityscapes数据集上，不同方法对照片→标签的分类性能。

5.1.4 损失函数分析

在表4和表5中，我们与我们的完整损失的消融进行了比较。移除 GAN 损失会显著降低结果，移除循环一致性损失也是如此。因此，我们得出结论，这两个术语对我们的结果都至关重要。我们还在只有一个方向的情况下评估了我们的方法的循环损失：GAN + 正向循环损失 $E_{x\sim p_{\text{data}}(x)}[||F(G(x))-x|{|}_1]$，或 GAN + 反向循环损失 $E_{y\sim p_{\text{data}}(y)}[||G(F(y))-y|{|}_1]$（公式 2），发现它往往会导致训练不稳定，并引发模式崩溃，尤其是被移除的映射方向。

表4： 消融研究：不同我们方法变体的FCN分数，在Cityscapes数据集上对标签→照片进行评估。

表5： 消融研究：不同损失函数对照片→标签的分类性能，在Cityscapes数据集上进行评估。

图7展示了一些定性示例。

图7： 在Cityscapes上训练的标签↔照片映射的不同变体。从左到右：输入，仅循环一致性损失，仅对抗损失，GAN + 正向循环一致性损失 ($F(G(x))\approx x$)，GAN + 反向循环一致性损失 ($G(F(y))\approx y$)，CycleGAN（我们的完整方法），和真实地面实况。仅Cycle和GAN + 反向都未能生成与目标域相似的图像。仅GAN和GAN + 正向都受到模式坍塌的困扰，产生与输入照片无关的相同标签映射。

5.1.5 图像重建质量

在图4中，我们展示了一些重建图像 $F(G(x))$ 的随机样本。我们观察到，这些重建图像往往与原始输入 $x$ 在训练和测试时都很接近，即使在一个域代表着更加多样的信息，比如地图↔航拍照片。

5.1.6 关于配对数据集的其他结果

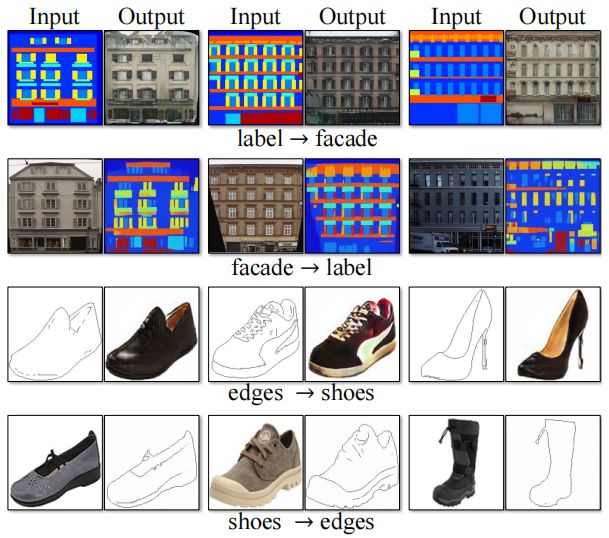
图8展示了在“pix2pix” [22] 中使用的其他配对数据集上的一些示例结果，例如从 CMP Facade Database [40] 中的建筑标签↔照片，以及从 UT Zappos50K 数据集 [60] 中的边缘↔鞋子。我们的结果的图像质量接近于完全监督的 pix2pix 所产生的结果，而我们的方法是在没有配对监督的情况下学习映射的。

图8： CycleGAN在“pix2pix”[22]中使用的配对数据集上的示例结果，例如建筑标签↔照片和边缘↔鞋子。

5.2 应用

我们在几个没有配对训练数据的应用领域展示了我们的方法。有关数据集的更多详细信息，请参考附录（第7节）。我们观察到，训练数据上的转换通常比测试数据上的转换更具吸引力，所有应用的完整结果（包括训练数据和测试数据）可以在我们的项目网站上查看。

集合风格转换（图10和图11） 我们在从 Flickr 和 WikiArt 下载的风景照片上训练模型。与“神经风格迁移” [13] 的最近工作不同，我们的方法学习了模仿整个艺术品收藏的风格，而不是转换单个选定的艺术品的风格。因此，我们可以学习以 Van Gogh 的风格生成照片，而不仅仅是以 Starry Night 的风格。每位艺术家/风格的数据集大小分别为 Cezanne（526）、Monet（1073）、Van Gogh（400）和 Ukiyo-e（563）。

图10： 艺术风格转换I：我们将输入图像转换为Monet、Van Gogh、Cezanne和Ukiyo-e的艺术风格。请访问我们的网站获取更多示例。

图11： 艺术风格转换II：我们将输入图像转换为Monet、Van Gogh、Cezanne和Ukiyo-e的艺术风格。请访问我们的网站获取更多示例。

物体变形（图13） 模型被训练以将一个 ImageNet [5] 类别的物体转换为另一个类别的物体（每个类别包含大约 1000 个训练图像）。Turmukhambetov 等人 [50] 提出了一个子空间模型，用于在相同类别之间将一个对象转换为另一个对象，而我们的方法专注于在两个视觉相似的类别之间进行物体变形。

图13： 我们的方法应用于多个翻译问题。这些图像被选择为相对成功的结果 - 请访问我们的网站获取更全面和随机的结果。在前两行中，我们展示了在马和斑马之间的物体转化问题上的结果，该问题在Imagenet [5]的野生马类别中有939张图像和斑马类别中有1177张图像上进行训练。还可以查看马→斑马的演示视频。中间两行展示了在冬季和夏季的Yosemite照片上进行的季节转换结果，这些照片来自Flickr。在底部两行，我们训练我们的方法使用了来自ImageNet的996张苹果图像和1020张脐橙图像。

季节转换（图13） 模型在从 Flickr 下载的 Yosemite 的 854 张冬季照片和 1273 张夏季照片上进行了训练。

从绘画中生成照片（图12） 对于绘画→照片，我们发现引入附加损失以鼓励映射保留输入和输出之间的颜色组成是有帮助的。具体而言，我们采用了 Taigman 等人 [49] 的技术，将生成器正则化为在将目标域的真实样本提供给生成器的输入时接近于恒等映射：即 $L_{\text{identity}}(G,F)=E_{y\sim p_{\text{data}}(y)}[||G(y)-y|{|}_1]+E_{x\sim p_{\text{data}}(x)}[||F(x)-x|{|}_1]$。在没有 Lidentity 的情况下，当没有必要时，生成器 G 和 F 可以自由地改变输入图像的色调。例如，在学习 Monet 的绘画与 Flickr 照片之间的映射时，生成器经常将白天的绘画映射到日落时拍摄的照片，因为在对抗性损失和循环一致性损失下，这样的映射可能同样有效。图9 展示了这个恒等映射损失的效果。

图12： 在将Monet的绘画转换为摄影风格方面相对成功的结果。请访问我们的网站获取更多示例。

图9： 在Monet的绘画→照片任务中，恒等映射损失的影响。从左到右：输入绘画，不带恒等映射损失的CycleGAN，带有恒等映射损失的CycleGAN。恒等映射损失有助于保留输入绘画的颜色。

在图12中，我们展示了将 Monet 的绘画转换为照片的其他结果。这个图和图9展示了在训练集中包含的绘画上的结果，而在论文中的所有其他实验中，我们只评估和展示了测试集上的结果。因为训练集中没有配对数据，对于训练集中的绘画来说，想出一个合理的转换是一个非常有挑战性的任务。确实，由于 Monet 不再能够创作新的绘画，对于看不见的“测试集”绘画的泛化并不是一个紧迫的问题。

照片增强（图14） 我们展示了我们的方法如何用于生成具有浅景深的照片。我们在从 Flickr 下载的花朵照片上训练了模型。源域包含由智能手机拍摄的花朵照片，通常由于小光圈而具有较深的景深。目标域包含由具有较大光圈的 DSLR 拍摄的照片。我们的模型成功地从智能手机拍摄的照片中生成了具有浅景深的照片。

图14： 照片增强：从一组智能手机快照映射到专业的DSLR照片，系统通常学会生成浅焦点效果。这里展示了我们测试集中最成功的一些结果 - 平均性能要差得多。请访问我们的网站以获取更全面和随机的示例。

与 Gatys 等人 [13] 的比较 在图15中，我们将我们的结果与神经风格迁移 [13] 在照片风格化方面进行了比较。对于每一行，我们首先使用两幅典型的艺术作品作为 [13] 的风格图像。另一方面，我们的方法可以在整个收藏风格中生成照片。为了将整个收藏的风格与神经风格迁移进行比较，我们计算了目标域中的平均格拉姆矩阵，并使用这个矩阵将 Gatys 等人的“平均风格”迁移到我们的方法上。

图15： 我们将我们的方法与神经风格转移[13]在照片风格化上进行了比较。从左到右：输入图像，使用两幅不同代表性艺术作品作为风格图像的Gatys等人的结果[13]，使用艺术家的整个收藏作为风格图像的Gatys等人的结果[13]，以及CycleGAN（我们的结果）。

图16对其他转换任务进行了类似的比较。我们观察到 Gatys 等人 [13] 需要找到与期望输出紧密匹配的目标风格图像，但仍经常无法产生逼真的结果，而我们的方法成功生成了类似目标领域的自然效果。

图16： 我们将我们的方法与神经风格转移[13]在各种应用上进行了比较。从上到下依次是：苹果→橙子，马→斑马，莫奈画作→照片。从左到右：输入图像，使用两幅不同图像作为风格图像的Gatys等人的结果[13]，使用目标域中的所有图像作为风格图像的Gatys等人的结果[13]，以及CycleGAN（我们的结果）。

6. 限制与讨论

尽管我们的方法在许多情况下可以取得令人信服的结果，但结果并不总是一致积极的。图17展示了一些典型的失败案例。在涉及颜色和纹理变化的转换任务中，就像上面报告的许多情况一样，该方法通常会成功。我们还尝试了需要几何变化的任务，但成功率很低。例如，在狗→猫的变形任务中，学习到的转换变得对输入进行最小的更改（图17）。这种失败可能是由于我们的生成器架构专门针对外观变化的良好性能而设计的。处理更多种类和极端变换，尤其是几何变化，是未来工作的一个重要问题。

图17： 我们方法的典型失败案例。左侧：在狗→猫变形的任务中，CycleGAN只能对输入进行最小的变化。右侧：在这个马→斑马的示例中，CycleGAN也失败了，因为我们的模型在训练时没有看到骑马的图像。更多综合性的结果请参见我们的网站。

一些失败案例是由于训练数据集的分布特征造成的。例如，我们的方法在马→斑马的例子中（图17，右侧）产生了混淆，因为我们的模型是在 ImageNet 的野马和斑马类别上训练的，该数据集中不包含人骑马或斑马的图像。

我们还观察到，配对训练数据所能达到的结果与我们的非配对方法所实现的结果之间存在差距。在某些情况下，这个差距可能非常难以弥补，甚至是不可能的：例如，我们的方法有时会在照片→标签任务的输出中对树木和建筑物的标签进行排列。解决这种歧义可能需要某种形式的弱语义监督。集成弱或半监督数据可能会导致更强大的转换器，但仍然只需一小部分完全监督系统的注释成本。

尽管如此，在许多情况下，完全非配对的数据是丰富可用的，应该加以利用。本文将推动在这种“无监督”设置中可能性的界限。

致谢：我们感谢 Aaron Hertzmann、Shiry Ginosar、Deepak Pathak、Bryan Russell、Eli Shechtman、Richard Zhang 和 Tinghui Zhou 对本文的许多有益评论。本工作部分得到了 NSF SMA-1514512、NSF IIS-1633310、谷歌研究奖、Intel 公司以及 NVIDIA 的硬件捐赠的支持。JYZ 获得了 Facebook 研究生奖学金的支持，TP 获得了三星奖学金的支持。用于风格转移的照片主要由 AE 拍摄于法国。

References

1. Y. Aytar, L. Castrejon, C. Vondrick, H. Pirsiavash, and A. Torralba. Cross-modal scene networks. PAMI, 2016.
2. K. Bousmalis, N. Silberman, D. Dohan, D. Erhan, and D. Krishnan. Unsupervised pixel-level domain adaptation with generative adversarial networks. In CVPR, 2017.
3. R. W. Brislin. Back-translation for cross-cultural research. Journal of cross-cultural psychology, 1(3):185–216, 1970.
4. M. Cordts, M. Omran, S. Ramos, T. Rehfeld, M. Enzweiler, R. Benenson, U. Franke, S. Roth, and B. Schiele. The cityscapes dataset for semantic urban scene understanding. In CVPR, 2016.
5. J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. Fei-Fei. Imagenet: A large-scale hierarchical image database. In CVPR, 2009.
6. E. L. Denton, S. Chintala, R. Fergus, et al. Deep generative image models using a Laplacian pyramid of adversarial networks. In NIPS, 2015.
7. J. Donahue, P. Kr¨ahenb¨uhl, and T. Darrell. Adversarial feature learning. In ICLR, 2017.
8. A. Dosovitskiy and T. Brox. Generating images with perceptual similarity metrics based on deep networks. In NIPS, 2016.
9. V. Dumoulin, I. Belghazi, B. Poole, A. Lamb, M. Arjovsky, O. Mastropietro, and A. Courville. Adversarially learned inference. In ICLR, 2017.
10. A. A. Efros and T. K. Leung. Texture synthesis by non-parametric sampling. In ICCV, 1999.
11. D. Eigen and R. Fergus. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. In ICCV, 2015.
12. L. A. Gatys, M. Bethge, A. Hertzmann, and E. Shechtman. Preserving color in neural artistic style transfer. arXiv preprint arXiv:1606.05897, 2016.
13. L. A. Gatys, A. S. Ecker, and M. Bethge. Image style transfer using convolutional neural networks. CVPR, 2016.
14. C. Godard, O. Mac Aodha, and G. J. Brostow. Unsupervised monocular depth estimation with left-right consistency. In CVPR, 2017.
15. I. Goodfellow. NIPS 2016 tutorial: Generative adversarial networks. arXiv preprint arXiv:1701.00160, 2016.
16. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio. Generative adversarial nets. In NIPS, 2014.
17. D. He, Y. Xia, T. Qin, L. Wang, N. Yu, T. Liu, and W.-Y. Ma. Dual learning for machine translation. In NIPS, 2016.
18. K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, 2016.
19. A. Hertzmann, C. E. Jacobs, N. Oliver, B. Curless, and D. H. Salesin. Image analogies. In SIGGRAPH, 2001.
20. G. E. Hinton and R. R. Salakhutdinov. Reducing the dimensionality of data with neural networks. Science, 313(5786):504–507, 2006.
21. Q.-X. Huang and L. Guibas. Consistent shape maps via semidefinite programming. In Symposium on Geometry Processing, 2013.
22. P. Isola, J.-Y. Zhu, T. Zhou, and A. A. Efros. Image-to-image translation with conditional adversarial networks. In CVPR, 2017.
23. J. Johnson, A. Alahi, and L. Fei-Fei. Perceptual losses for real-time style transfer and super-resolution. In ECCV, 2016.
24. Z. Kalal, K. Mikolajczyk, and J. Matas. Forward-backward error: Automatic detection of tracking failures. In ICPR, 2010.
25. L. Karacan, Z. Akata, A. Erdem, and E. Erdem. Learning to generate images of outdoor scenes from attributes and semantic layouts. arXiv preprint arXiv:1612.00215, 2016.
26. D. Kingma and J. Ba. Adam: A method for stochastic optimization. In ICLR, 2015.
27. D. P. Kingma and M. Welling. Auto-encoding variational Bayes. ICLR, 2014.
28. P.-Y. Laffont, Z. Ren, X. Tao, C. Qian, and J. Hays. Transient attributes for high-level understanding and editing of outdoor scenes. ACM TOG, 33(4):149, 2014.
29. C. Ledig, L. Theis, F. Huszár, J. Caballero, A. Cunningham, A. Acosta, A. Aitken, A. Tejani, J. Totz, Z. Wang, et al. Photo-realistic single image super-resolution using a generative adversarial network. In CVPR, 2017.
30. C. Li and M. Wand. Precomputed real-time texture synthesis with Markovian generative adversarial networks. ECCV, 2016.
31. M.-Y. Liu, T. Breuel, and J. Kautz. Unsupervised image-to-image translation networks. In NIPS, 2017.
32. M.-Y. Liu and O. Tuzel. Coupled generative adversarial networks. In NIPS, 2016.
33. J. Long, E. Shelhamer, and T. Darrell. Fully convolutional networks for semantic segmentation. In CVPR, 2015.
34. A. Makhzani, J. Shlens, N. Jaitly, I. Goodfellow, and B. Frey. Adversarial autoencoders. In ICLR, 2016.
35. X. Mao, Q. Li, H. Xie, R. Y. Lau, Z. Wang, and S. P. Smolley. Least squares generative adversarial networks. In CVPR. IEEE, 2017.
36. M. Mathieu, C. Couprie, and Y. LeCun. Deep multi-scale video prediction beyond mean square error. In ICLR, 2016.
37. M. F. Mathieu, J. Zhao, A. Ramesh, P. Sprechmann, and Y. LeCun. Disentangling factors of variation in deep representation using adversarial training. In NIPS, 2016.
38. D. Pathak, P. Krahenbuhl, J. Donahue, T. Darrell, and A. A. Efros. Context encoders: Feature learning by inpainting. CVPR, 2016.
39. A. Radford, L. Metz, and S. Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. In ICLR, 2016.
40. R. ˇS. Radim Tyleˇcek. Spatial pattern templates for recognition of objects with regular structure. In Proc. GCPR, Saarbrucken, Germany, 2013.
41. S. Reed, Z. Akata, X. Yan, L. Logeswaran, B. Schiele, and H. Lee. Generative adversarial text to image synthesis. In ICML, 2016.
42. R. Rosales, K. Achan, and B. J. Frey. Unsupervised image translation. In ICCV, 2003.
43. T. Salimans, I. Goodfellow, W. Zaremba, V. Cheung, A. Radford, and X. Chen. Improved techniques for training GANs. In NIPS, 2016.
44. P. Sangkloy, J. Lu, C. Fang, F. Yu, and J. Hays. Scribbler: Controlling deep image synthesis with sketch and color. In CVPR, 2017.
45. Y. Shih, S. Paris, F. Durand, and W. T. Freeman. Data-driven hallucination of different times of day from a single outdoor photo. ACM TOG, 32(6):200, 2013.
46. A. Shrivastava, T. Pfister, O. Tuzel, J. Susskind, W. Wang, and R. Webb. Learning from simulated and unsupervised images through adversarial training. In CVPR, 2017.
47. K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. In ICLR, 2015.
48. N. Sundaram, T. Brox, and K. Keutzer. Dense point trajectories by GPU-accelerated large displacement optical flow. In ECCV, 2010.
49. Y. Taigman, A. Polyak, and L. Wolf. Unsupervised cross-domain image generation. In ICLR, 2017.
50. D. Turmukhambetov, N. D. Campbell, S. J. Prince, and J. Kautz. Modeling object appearance using context-conditioned component analysis. In CVPR, 2015.
51. M. Twain. The jumping frog: in English, then in French, and then clawed back into a civilized language once more by patient. Unremunerated Toil, 3, 1903.
52. D. Ulyanov, V. Lebedev, A. Vedaldi, and V. Lempitsky. Texture networks: Feed-forward synthesis of textures and stylized images. In ICML, 2016.
53. D. Ulyanov, A. Vedaldi, and V. Lempitsky. Instance normalization: The missing ingredient for fast stylization. arXiv preprint arXiv:1607.08022, 2016.
54. C. Vondrick, H. Pirsiavash, and A. Torralba. Generating videos with scene dynamics. In NIPS, 2016.
55. F. Wang, Q. Huang, and L. J. Guibas. Image co-segmentation via consistent functional maps. In ICCV, 2013.
56. X. Wang and A. Gupta. Generative image modeling using style and structure adversarial networks. In ECCV, 2016.
57. J. Wu, C. Zhang, T. Xue, B. Freeman, and J. Tenenbaum. Learning a probabilistic latent space of object shapes via 3D generative-adversarial modeling. In NIPS, 2016.
58. S. Xie and Z. Tu. Holistically-nested edge detection. In ICCV, 2015.
59. Z. Yi, H. Zhang, T. Gong, Tan, and M. Gong. Dual-GAN: Unsupervised dual learning for image-to-image translation. In ICCV, 2017.
60. A. Yu and K. Grauman. Fine-grained visual comparisons with local learning. In CVPR, 2014.
61. C. Zach, M. Klopschitz, and M. Pollefeys. Disambiguating visual relations using loop constraints. In CVPR, 2010.
62. R. Zhang, P. Isola, and A. A. Efros. Colorful image colorization. In ECCV, 2016.
63. J. Zhao, M. Mathieu, and Y. LeCun. Energy-based generative adversarial network. In ICLR, 2017.
64. T. Zhou, P. Krahenbuhl, M. Aubry, Q. Huang, and A. A. Efros. Learning dense correspondence via 3D-guided cycle consistency. In CVPR, 2016.
65. T. Zhou, Y. J. Lee, S. Yu, and A. A. Efros. Flowweb: Joint image set alignment by weaving consistent, pixel-wise correspondences. In CVPR, 2015.
66. J.-Y. Zhu, P. Kr¨ahenb¨uhl, E. Shechtman, and A. A. Efros. Generative visual manipulation on the natural image manifold. In ECCV, 2016.

7. 附录

7.1. 训练细节

我们从头开始训练网络，初始学习率为0.0002。在实际操作中，我们在优化鉴别器D时将目标减半，以减缓D的学习速度相对于G的速度。在前100个epoch内保持相同的学习率，然后再接下来的100个epoch中线性地将学习率衰减至零。权重初始化为高斯分布N(0, 0.02)。

Cityscapes标签↔照片：从Cityscapes训练集[4]中获取了2975张大小为128×128的训练图像。用Cityscapes验证集进行了测试。

地图↔航拍照片：从Google Maps [22]上获取了1096张大小为256×256的训练图像。这些图像来自纽约市及其周边地区。根据采样区域的中位纬度，将数据分为了训练集和测试集（添加了缓冲区域，以确保测试集中不包含训练像素）。

建筑立面标签↔照片：从CMP Facade Database [40]中获取了400张训练图像。

边缘→鞋：从UT Zappos50K数据集[60]中获取了约50000张训练图像。模型进行了5个epochs的训练。

马↔斑马和苹果↔橙子：使用ImageNet [5]下载了野生马、斑马、苹果和橙子的图像。这些图像被缩放到256×256像素。每个类别的训练集大小分别为939（马）、1177（斑马）、996（苹果）和1020（橙子）。

夏季↔冬季优胜美地：使用Flickr API并搜索标签yosemite和date-taken字段，下载了这些图像。去除了黑白照片。这些图像被缩放到256×256像素。每个类别的训练集大小分别为1273（夏季）和854（冬季）。

照片↔艺术样式转换：从Wikiart.org下载了艺术图像。手动剔除了一些素描或过于露骨的艺术品。从Flickr上使用标签landscape和landscapephotography下载了照片。去除了黑白照片。这些图像被缩放到256×256像素。每个类别的训练集大小分别为1074（莫奈）、584（塞尚）、401（梵高）、1433（浮世绘）和6853（照片）。莫奈的数据集被特别修剪，只包括了风景画，而梵高的数据集只包括他后期最具辨识度的艺术风格。

莫奈的画作→照片：为了实现高分辨率并节省内存，我们对原始图像进行了随机正方形裁剪。为了生成结果，我们将宽度为512像素且符合正确长宽比的图像传递给生成器网络作为输入。恒等映射损失的权重为0.5λ，其中λ是循环一致性损失的权重。我们设置λ = 10。

花卉照片增强：从Flickr上下载了使用Apple iPhone 5、5s或6拍摄的花卉图像，通过搜索标签flower获得。还通过搜索标签flower、dof从Flickr上下载了具有浅景深的单反相机图像。这些图像的宽度被缩放到360像素。恒等映射损失的权重为0.5λ。智能手机和单反相机数据集的训练集大小分别为1813和3326。我们设置 $\lambda =10$。

7.2. 网络架构

以下是生成器和鉴别器的网络架构。我们提供了PyTorch和Torch实现。

生成器架构：我们采用了Johnson等人的架构 [23]。对于128×128的训练图像，我们使用6个残差块，对于256×256或更高分辨率的训练图像，我们使用9个残差块。以下是我们遵循Johnson等人GitHub存储库中使用的命名约定。

• c7s1-k：具有k个过滤器和步长1的7×7卷积-实例标准化-ReLU层。
• dk：具有k个过滤器和步长2的3×3卷积-实例标准化-ReLU层。
• Rk：残差块，包含两个具有相同过滤器数量的3×3卷积层。
• uk：具有k个过滤器和步长1/2的3×3分数步幅卷积-实例标准化-ReLU层。

使用6个残差块的网络如下：

c7s1-64,d128,d256,R256,R256,R256,
R256,R256,R256,u128,u64,c7s1-3

使用9个残差块的网络如下：

c7s1-64,d128,d256,R256,R256,R256,
R256,R256,R256,R256,R256,R256,u128
u64,c7s1-3

鉴别器架构：对于鉴别器网络，我们使用70×70的PatchGAN [22]。Ck表示具有k个过滤器和步长2的4×4卷积-实例标准化-LeakyReLU层。在最后一层之后，我们应用卷积来产生一维输出。我们不在第一个C64层使用实例标准化。我们使用斜率为0.2的Leaky ReLUs。鉴别器架构如下：

C64-C128-C256-C512

准化-ReLU层。

使用6个残差块的网络如下：

c7s1-64,d128,d256,R256,R256,R256,
R256,R256,R256,u128,u64,c7s1-3

使用9个残差块的网络如下：

c7s1-64,d128,d256,R256,R256,R256,
R256,R256,R256,R256,R256,R256,u128
u64,c7s1-3

鉴别器架构：对于鉴别器网络，我们使用70×70的PatchGAN [22]。Ck表示具有k个过滤器和步长2的4×4卷积-实例标准化-LeakyReLU层。在最后一层之后，我们应用卷积来产生一维输出。我们不在第一个C64层使用实例标准化。我们使用斜率为0.2的Leaky ReLUs。鉴别器架构如下：

C64-C128-C256-C512

---

1. 我们通常出于简化的目的省略下标 i 和 j。 ↩︎

2. 我们在所有模型上使用256×256的图像进行训练，而在pix2pix [22] 中，该模型是在512×512图像的256×256块上进行训练，并在测试时在512×512图像上以卷积方式运行。在我们的实验中，我们选择了256×256的图像，因为许多基线模型无法扩展到高分辨率图像，而且CoGAN无法进行完全卷积测试。 ↩︎

3. 我们还在512×512的分辨率下训练了CycleGAN和pix2pix，并观察到相当的性能表现：地图→航拍照片：CycleGAN：37.5% ± 3.6%，pix2pix：33.9% ± 3.1%；航拍照片→地图：CycleGAN：16.5% ± 4.1%，pix2pix：8.5% ± 2.6%。 ↩︎