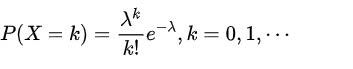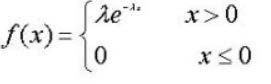numpy入门2：随机抽样

numpy.seed()

numpy.random.seed(seed=None) 

用于指定随机数生成时所用算法开始的整数值，如果使用相同的seed()值，则每次生成的随机数都相同。

如果不设置这个值，则系统根据时间来自己选择这个值，此时每次生成的随机数因时间差异而不同。

在对数据进行预处理时，经常加入新的操作或改变处理策略，此时如果伴随着随机操作，最好还是指定唯一的随机种子.

避免由于随机的差异对结果产生影响。

影响范围

随机数种子对后面的结果一直有影响。

后面是指在同一个cell里面。如果不在同一个cell里面，np.random.seed()对其他随机函数没有束缚力。

【例如】

• 每一次的执行结果一样（在同一个cell内）

import numpy as np
np.random.seed(0)
np.random.randint(4)

• 每一次的执行结果不一样（分开两个cell）

import numpy as np
np.random.seed(0)

np.random.randint(4)

离散型随机变量

二项分布

1. 定义：二项分布可以用于只有一次实验只有两种结果，各结果对应的概率相等的多次实验的概率问题。
2. 二项分布概率函数的数学表示
   
3. 代码

numpy.random.binomial(n, p, size=None)

• size:采样次数（做实验的次数）
• n：做了n重伯努利试验（有多少个个体来做实验）
• p:成功的概率

【例如】
野外正在进行9（n=9）口石油勘探井的发掘工作，每一口井能够开发出油的概率是0.1（p=0.1）。请问，最终所有的勘探井都勘探失败的概率？

numpy.random.binomial(n, p, size=None)

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(20200605)
n = 9
p = 0.1
size = 50000
#x是实验5000次结果的一个元组
x = np.random.binomial(n, p, size)
print(np.sum(x == 0)/size)
print(np.sum(x == 1)/size)
print(np.sum(x == 2)/size)
print(np.sum(x == 3)/size)
print(np.sum(x == 4)/size)
print(np.sum(x == 5)/size)
print(np.sum(x == 6)/size)
print(np.sum(x == 7)/size)
print(np.sum(x == 8)/size)
print(np.sum(x == 9)/size)
#0.3897
#0.38502
#0.17206
#0.04484
#0.00744
#0.00082
#0.00012
#0.0
#0.0
#0.0

plt.hist(x)
plt.xlabel('随机变量：成功次数')
plt.ylabel('样本中出现的次数')
plt.show()
s = stats.binom.pmf(range(10), n, p)
print(np.around(s, 3))

泊松分布

1. 定义
   估计某个时段某事件发生的概率。
2. 代码实现

poisson.pmf(k) = exp(-lam)lam*k/k!

3. 数学表达式
   

numpy.random.poisson(lam = 1.0, size = None)

• size:采样次数
• lam：一个单位内事件发生的平均值
• 返回值：一个单位内事件发生的次数
  【例如】
  假定某航空公司预定票处平均每小时接到42次订票电话，那么10分钟内恰好接到6次电话的概
  率是多少？

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# 为matplotlib添加中文库
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

np.random.seed(20201125)
#以10分钟为一个单位
lam = 42/6
size = 50000
x = np.random.poisson(lam,size)
#或者
# x = stats.poisson.rvs(lam,size = size)
print(np.sum(x == 6)/size)

plt.hist(x)
plt.xlabel('随机变量：每十分钟接到订票电话的次数')
plt.ylabel('50000个样本中出现的次数')
plt.show()

#用poisson.pmf(k, mu)求对应分布的概率:概率质量函数 (PMF)
x = stats.poisson.pmf(6, lam)
print(x)

超几何分布

1. 定义
   超几何分布中，各次士妍不是独立的，各次实验成功的概率也不等。
2. 数学表达式
   
3. 代码实现

numpy.random.hypergeometric(ngood,nbad,nsample,size = None)

• size:采样次数
• ngood：总体具有成功标志的元素个数
• nbad：总体中不具有成功标志的元素个数
• ngood+nbad：表示总体样本容量
• nsample：表示抽取元素的次数（小于或等于总体样本容量）
• 返回值：抽取nsample个元素中具有成功表示的元素个数

【例如】一共20只动物里有7只是狗，抽取12只有3只狗的概率（无放回抽样）。

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

np.random.seed(20201125)
ngood = 7
nbad = 13
size = 50000
nsample = 12
x = np.random.hypergeometric(ngood = 7,nbad = 13,nsample = 12,size = size)
print(np.sum(x == 3)/size)

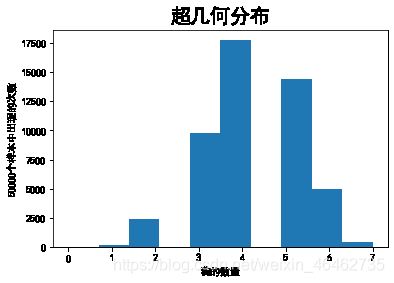
plt.hist(x)
plt.xlabel('狗的数量')
plt.ylabel('50000个样本中出现的次数')
plt.title('超几何分布',fontsize = 20)
plt.show()

x = range(8)
#用hypergeom.pmf(k, M, n, N, loc)来计算k次成功的概率
s = stats.hypergeom.pmf(k=x, M=20, n=7, N=12)
print(np.round(s, 3)) 

连续型随机变量

均匀分布

numpy.random.uniform(low = 0.0,high = 1.0,size =None)

【例如】
在low到high范围内，创建大小为size的均匀分布的随机数。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(20201125)
low = 0
high = 1
size = 50000
x = np.random.uniform(low,high,size = size)

plt.hist(x,bins = 20)
plt.show()

a = stats.uniform.cdf(10, 0, 100)
b = stats.uniform.cdf(50, 0, 100)
print(b ‐ a)

作为uniform() 的特列，可以得到[0,1) 之间的均匀分布的随机数。

numpy.random.rand(do,d1,....,dn)

【例如】根据指定大小产生[0,1)之间均匀分布的随机数。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(20201125)
#等价
np.random.rand(5)
np.random.uniform(size = 5)
np.random.rand((4,5))
np.random.uniform(size = (4,5))

作为uniform 的另一特例，可以得到[low,high) 之间均匀分布的随机整数。

numpy.random.randint(low,high = None,size = None,dtype = '1')

正态分布

1. 数学表达
   

2. 代码实现

numpy.random.randn(d0,d1,....,dn)

【例如】根据指定大小产生满足标准正态分布的数组（均值为0，标准差为1）。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

np.random.seed(20201125)
size = 50000
x = np.random.randn(size)
y1 = (np.sum(x<1) - np.sum(x<-1))/size
y2 = (np.sum(x < 2) ‐ np.sum(x < ‐2)) / size
y3 = (np.sum(x < 3) ‐ np.sum(x < ‐3)) / size
print(y1) 
print(y2)
print(y3)
#六西格玛

plt.hist(x,bins = 20)
plt.show()

y1 = stats.norm.cdf(1) ‐ stats.norm.cdf(‐1)
y2 = stats.norm.cdf(2) ‐ stats.norm.cdf(‐2)
y3 = stats.norm.cdf(3) ‐ stats.norm.cdf(‐3)
print(y1) 
print(y2) 
print(y3)

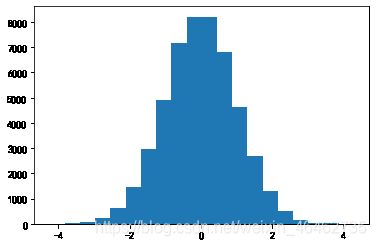
还可以指定分布以及所需参数来进行随机，例如高斯分布中的mu和sigma。

numpy.random.normal(loc = 0,scale = 1,size = None)
sigma*numpy.random.randn(....)+mu

指数分布

1. 数学表达式
   
2. 代码实现

numpy.random.exponential(scale = 1,size = None)

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(20201125)
lam = 7
size = 50000
x = np.random.exponential(1/lam,size)
plt.hist(x,bins = 20)
plt.show()

其他随机函数

随机从序列中获取元素

从序列中获取元素，若a为整数，元素取值从np.range(a) 中随机获取；若a为数组，取值从a 数组元素中随机获取。

该函数还可以控制生成数组中的元素是否重复replace ，以及选取元素的概率p（选取数组中的元素的概率）。

numpy.random.choice(a,size=None,replace=True,p = None)

• a:数组/整数
• size:抽取元素的数量
• replace:True是可重复，False是不可重复
• p:选取数组中的元素的概率

import numpy as np
np.random.seed(20201125)
x = np.random.choice(10,3,p=[0.05, 0, 0.05, 0.9, 0, 0, 0, 0, 0, 0])
print(x)
aa_milne_arr = ['pooh', 'rabbit', 'piglet', 'Christopher']
x = np.random.choice(aa_milne_arr, 5, p=[0.5, 0.1, 0.1, 0.3])
print(x)

对数据集进行洗牌操作

数据一般都是按照采集顺序排列的，但是在机器学习中很多算法都要求数据之间相互独立，所以需要先对数据集进行洗牌操作。
对x进行重排序，如果x为多维数组，只沿第 0 轴洗牌
改变原来的数组，输出为None。

numpy.random.shuffle(x)

import numpy as np
a = np.arange(10)
np.random.shuffle(a)
a

print(np.random.shuffle([1, 4, 9, 12, 15]))
# None

permutation() 函数的作用与shuffle() 函数相同，可以打乱第0轴的数据，但是它不会改变原来的数组。

numpy.random.permutation(x)

import numpy as np
np.random.seed(20200614)
x = np.arange(10)
y = np.random.permutation(x)
print(y)

print(np.random.permutation([1, 4, 9, 12, 15]))
# [ 4 1 9 15 12]