acdream1075 神奇的%系列三（线代-矩阵-数论）

题目链接：http://115.28.76.232/problem?pid=1075

题意：定义一个f(n)函数，f(n) = a * f(n - 1) + b * f(n - 2), f(1) = c, f(2) = d.问f(n)在模1000000007情况下的最小循环节。即求最小的m，使对任意的n有f(n) % 1000000007 = f(n + m) % 1000000007.

思路：

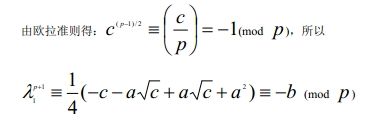
i64 p[] = {2, 3, 7, 109, 167, 500000003};

i64 cnt[]   = {4, 2, 1, 2,   1,   1        };



i64 a,b,c,d;



int judge(i64 x)

{

    if(myPow(x,(mod-1)>>1,mod)==1) return 1;

    return -1;

}



int ok(i64 n)

{

    Matrix A;

    A.init(0);

    A.a[0][0]=a;

    A.a[0][1]=b;

    A.a[1][0]=1;

    A.a[1][1]=0;



    A=A.Pow(n);



    i64 cc=(A.a[0][0]*c%mod+A.a[0][1]*d%mod)%mod;

    i64 dd=(A.a[1][0]*c%mod+A.a[1][1]*d%mod)%mod;

    return cc==c&&dd==d;

}



i64 ans;



void DFS(i64 cur,int dep)

{

    if(dep==6)

    {

        if(ok(cur)&&(ans==-1||cur<ans))  ans=cur;

        return;

    }

    int i;

    for(i=0;i<=cnt[dep];i++)

    {

        DFS(cur,dep+1);

        cur*=p[dep];

    }

}



int main()

{

    while(cin>>a>>b>>c>>d)

    {

        ans=-1;

        if(judge(a*a+4*b)==1)

        {

            if(ok(1)) ans=1;

            else if(ok(2)) ans=2;

            else if(ok(500000003)) ans=500000003;

            else if(ok(mod-1)) ans=mod-1;

        }

        else

        {

            DFS(1,0);

        }

        printf("%lld\n",ans);

    }

}