R语言矩阵的相关计算
R语言矩阵的相关计算
- 矩阵的转置
- 矩阵的乘法
- 特征值和特征向量
- 行列式的值
- 求逆矩阵
-
- 方法一:
- 方法二：
- 求矩阵线性方程组
- 求解伴随矩阵
-
- 使用for循环
-
- 验证
- 使用 adjoint函数
矩阵的转置
例：求下列矩阵的转置
b = [ 1 5 6 2 4 2 5 8 9 ] b=\left[ \begin{matrix} 1& 5& 6\\ 2& 4& 2\\ 5& 8& 9\\ \end{matrix} \right] b=⎣⎡125548629⎦⎤
这里我们用到t函数
a <- c(1,5,6,
4,8,2,
5,8,9)
b <- matrix(a,nc=3,byrow=T);b
t(b)
输出结果：
矩阵的乘法
使用a%*%b表示矩阵ab的乘积，这里介绍第二种方法
crossprod（X,Y）计算 X T Y X^TY XTY
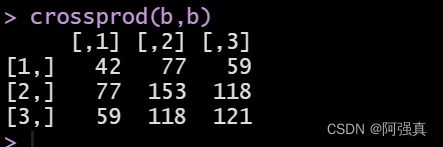
计算 b T b b^Tb bTb
crossprod(b,b)
计算 b b T bb^T bbT
bt <- t(b);bt#首先计算出转置
crossprod(bt,bt)
计算 b ∗ b b*b b∗b
bt <- t(b);bt
crossprod(bt,b)
特征值和特征向量
用到eigen函数
eigen(b)
行列式的值
用到det函数
det(b)
求逆矩阵
方法一:
solve（A，B）可以求解 A X = B AX=B AX=B ,当只有A时，即solve（A）表示求 A X = E AX=E AX=E,即求A的逆矩阵
求 A = [ 1 1 1 2 − 1 − 3 4 1 9 ] 的逆矩阵 \text{求}A=\left[ \begin{matrix} 1& 1& 1\\ 2& -1& -3\\ 4& 1& 9\\ \end{matrix} \right] \text{的逆矩阵} 求A=⎣⎡1241−111−39⎦⎤的逆矩阵
A<- c(1,1,1,
2,-1,-3,
4,1,9)
A <- matrix(ab,nc=3,byrow=T)
solve(A)
方法二：
使用MASS包里的ginv函数
library(MASS)
ginv(A)
求矩阵线性方程组
solve（A，B）可以求解 A X = B AX=B AX=B ,当只有A时，即solve（A）表示求 A X = E AX=E AX=E,即求A的逆矩阵
x 1 + x 2 + x 3 = 1 2 x 1 − x 2 − 3 x 3 = 0 4 x 1 + x 2 + 9 x 3 = 0 x_1+x_2+x_3=1 \\ 2x_1-x_2-3x_3=0 \\ 4x_1+x_2+9x_3=0 x1+x2+x3=12x1−x2−3x3=04x1+x2+9x3=0
这个系数矩阵就是上面的A
A<- c(1,1,1,
2,-1,-3,
4,1,9)
A <- matrix(A,nc=3,byrow=T)
B <- c(1,0,0)
B<- t(B)
solve(A,B)
即 x 1 = 0.2 , x 2 = 1 , x 3 = − 0.2 x_1=0.2,x_2=1,x_3=-0.2 x1=0.2,x2=1,x3=−0.2
求解伴随矩阵
求 a = [ 1 1 1 2 − 1 − 3 4 1 9 ] 的伴随矩阵 \text{求}a=\left[ \begin{matrix} 1& 1& 1\\ 2& -1& -3\\ 4& 1& 9\\ \end{matrix} \right] \text{的伴随矩阵} 求a=⎣⎡1241−111−39⎦⎤的伴随矩阵
a<- c(1,1,1,
2,-1,-3,
4,1,9)
a <- matrix(A,nc=3,byrow=T)
这里我没有找到求解伴随矩阵的函数，如果有知道的，请在评论区告知，谢谢
使用for循环
根据伴随矩阵的定义，我们可以简单的写个for循环语句来求解
A ∗ = [ A 11 A 21 A 31 A 12 A 22 A 32 A 13 A 23 A 33 ] = ( A i j ) T A^{\ast}=\left[ \begin{matrix} A_{11}& A_{21}& A_{31}\\ A_{12}& A_{22}& A_{32}\\ A_{13}& A_{23}& A_{33}\\ \end{matrix} \right] =\left( A_{ij} \right) ^T A∗=⎣⎡A11A12A13A21A22A23A31A32A33⎦⎤=(Aij)T
D<- matrix(0,nc=3,nr=3);D#首先创建一个3×3的0矩阵
for ( i in 1:3){
for(j in 1:3)
D[i,j] <- (-1)^(i+j)*det(a[-j,-i])
}
D
- 第一次写的时候出现了错误，原因是伴随矩阵的 A i j A_{ij} Aij是代数余子式而不是余子式，这就导致了我少添加了 ( − 1 ) i + j (-1)^{i+j} (−1)i+j 次方
验证
若 A ∗ A^{\ast} A∗是矩阵A的伴随矩阵，根据伴随矩阵的性质有
A A ∗ = A ∗ A = ∣ A ∣ E AA^{\ast}=A^{\ast}A=\left| A \right|E AA∗=A∗A=∣A∣E
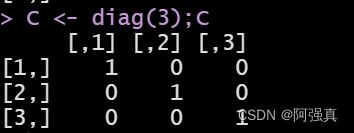
首先用diag函数创建一个3阶单位阵
C <- diag(3);C
首先计算 a ∗ D 和 D ∗ a 即 验 证 A A ∗ = A ∗ A a*D和D*a即验证AA^{\ast}=A^{\ast}A a∗D和D∗a即验证AA∗=A∗A
a%*%D
D%*%a
可以看出两个结果是一致的，但是当我使用逻辑语言时，出来的却是两个不相等，每一个对应的都是false
a%*%D==D%*%a
这是因为，因为什么呢，我也说不清楚
不过当我们对每一个数都保留两位小数的时候，再次判断，这时候就正确了
round(a%*%D,2)==round(D%*%a,2)
在验证 A ∗ A = ∣ A ∣ E A^{\ast}A=\left| A \right|E A∗A=∣A∣E
m <- det(a)*C
round(a%*%D,2)==round(m,2)
同样对结果保留两位小数，这就是正确的了
验证成功
使用 adjoint函数
这里自己编写了一个函数，复制下面代码运行一下即可使用此函数
adjoint <- function(x){
n <- sqrt(length(x))
y <- matrix(0,nc=n,nr=n)
for ( i in 1:n)
for ( j in 1:n)
y[i,j] <- (-1)^(i+j)*det(x[-j,-i])
y
}
如果想求A的伴随矩阵，只需要adjoint（A）即可
例：
adjoint(a)
