【3D激光SLAM】LOAM源代码解析--laserMapping.cpp

系列文章目录

·【3D激光SLAM】LOAM源代码解析–scanRegistration.cpp
·【3D激光SLAM】LOAM源代码解析–laserOdometry.cpp
·【3D激光SLAM】LOAM源代码解析–laserMapping.cpp
·【3D激光SLAM】LOAM源代码解析–transformMaintenance.cpp

---

写在前面

本系列文章将对LOAM源代码进行讲解，在讲解过程中，涉及到论文中提到的部分，会结合论文以及我自己的理解进行解读，尤其是对于其中坐标变换的部分，将会进行详细的讲解。

本来是懒得写的，一个是怕自己以后忘了，另外是我在学习过程中，其实没有感觉哪一个博主能讲解的通篇都能让我很明白，特别是坐标变换部分的代码，所以想着自己学完之后，按照自己的理解，也写一个LOAM解读，希望能对后续学习LOAM的同学们有所帮助。

之后也打算录一个LOAM讲解的视频，大家可以关注一下。

---

---

整体框架

LOAM多牛逼就不用多说了，直接开始

先贴一下我详细注释的LOAM代码，在这个版本的代码上加入了我自己的理解。

我觉得最重要也是最恶心的一部分是其中的坐标变换，在代码里面真的看着头大，所以先明确一下坐标系(都是右手坐标系)：

• IMU(IMU坐标系imu)：x轴向前，y轴向左，z轴向上
• LIDAR(激光雷达坐标系l)：x轴向前，y轴向左，z轴向上
• CAMERA(相机坐标系，也可以理解为里程计坐标系c)：z轴向前，x轴向左，y轴向上
• WORLD(世界坐标系w，也叫全局坐标系，与里程计第一帧init重合)：z轴向前，x轴向左，y轴向上
• MAP(地图坐标系map，一定程度上可以理解为里程计第一帧init)：z轴向前，x轴向左，y轴向上

坐标变换约定： 为了清晰，变换矩阵的形式与《SLAM十四讲中一样》，即：$R_{A\_B}$表示B坐标系相对于A坐标系的变换，B中一个向量通过$R_{A\_B}$可以变换到A中的向量。

首先对照ros的节点图和论文中提到的算法框架来看一下：

可以看到节点图和论文中的框架是一一对应的，这几个模块的功能如下：

• scanRegistration：对原始点云进行预处理，计算曲率，提取特征点
• laserOdometry：对当前sweep与上一次sweep进行特征匹配，计算一个快速(10Hz)但粗略的位姿估计
• laserMapping：对当前sweep与一个局部子图进行特征匹配，计算一个慢速(1Hz)比较精确的位姿估计
• transformMaintenance：对两个模块计算出的位姿进行融合，得到最终的精确地位姿估计

本文介绍laserMapping模块，它相当于SLAM的后端，它维护了一个局部地图，它相当于一个scan-to-map的匹配过程，它的具体功能如下：

1. 接收特征点话题、全部点云话题、IMU话题，并保存到对应的变量中
2. 将当前sweep与上几次sweep(局部地图)进行特征匹配，得到edge point在局部子图中KD-tree查找到的5个最近点以及planar point在局部子图KD-tree查找到的5个最近点
3. 计算edge point对应5个点构成的均值和协方差矩阵，对协方差矩阵进行分解，求解匹配到的直线参数
4. 用planar point对应5个点构建一个超定方程组，求解得到平面参数
5. 构建雅可比矩阵和残差项，求解优化后的位姿变换
6. 将当前帧的点云插入局部子图，维护一个局部地图，用于下一帧的匹配
7. 发布话题并更新tf变换

---

一、变量含义

首先，介绍一下本程序用到变量的含义，理解这一部分非常重要：

• transformBefMapped[6]：经过laserMapping模块优化前的，上一帧相对于初始时刻的位姿变换$T_{init\_start}$
• transformSum[6]：从laserOdometry模块接收到的，当前帧相对于初始时刻的变换$T_{init\_start}$
• transformAftMapped[6]：经过laserMapping模块优化后的，当前帧相对于初始时刻的位姿变换$T_{map\_end}$，在优化之前存储的事上一帧相对于初始时刻的位姿变换$T_{map\_start}$
• transformTobeMapped[6]：在laserMapping模块中用于优化的变量，优化完成后会赋值给transformAftMapped[6]

一些理解：虽然transformAftMapped[6]我上面写的是$T_{map\_end}$，看起来好像是把坐标系换成了map坐标系，但是我觉得这里有两种理解都可以：

1. AftMapped可以理解为经过laserMapping模块优化后的里程计坐标系下的当前帧end相对于初始帧的坐标变换
2. 也可以理解为经过laserMapping模块优化，变到了map坐标系

二、main()函数以及回调函数

main()函数是很简单的，就是定义了一系列的发布者和订阅者，订阅了来自laserOdometry节点发布的话题和imu数据话题；然后定义了一个tf发布器，发布经过mapping模块优化后的当前帧(/aft_mapped)到初始帧(/camera_init)的坐标变换；然后定义了一些列下面会用到的变量。

其中有5个订阅者，分别看一下它们的回调函数。

int main(int argc, char** argv)
{
  ros::init(argc, argv, "laserMapping");
  ros::NodeHandle nh;

  ros::Subscriber subLaserCloudCornerLast = nh.subscribe<sensor_msgs::PointCloud2>
                                            ("/laser_cloud_corner_last", 2, laserCloudCornerLastHandler);

  ros::Subscriber subLaserCloudSurfLast = nh.subscribe<sensor_msgs::PointCloud2>
                                          ("/laser_cloud_surf_last", 2, laserCloudSurfLastHandler);

  ros::Subscriber subLaserOdometry = nh.subscribe<nav_msgs::Odometry> 
                                     ("/laser_odom_to_init", 5, laserOdometryHandler);

  ros::Subscriber subLaserCloudFullRes = nh.subscribe<sensor_msgs::PointCloud2> 
                                         ("/velodyne_cloud_3", 2, laserCloudFullResHandler);

  ros::Subscriber subImu = nh.subscribe<sensor_msgs::Imu> ("/imu/data", 50, imuHandler);

  ros::Publisher pubLaserCloudSurround = nh.advertise<sensor_msgs::PointCloud2> 
                                         ("/laser_cloud_surround", 1);

  ros::Publisher pubLaserCloudFullRes = nh.advertise<sensor_msgs::PointCloud2> 
                                        ("/velodyne_cloud_registered", 2);

  ros::Publisher pubOdomAftMapped = nh.advertise<nav_msgs::Odometry> ("/aft_mapped_to_init", 5);
  nav_msgs::Odometry odomAftMapped;
  odomAftMapped.header.frame_id = "/camera_init";
  odomAftMapped.child_frame_id = "/aft_mapped";

  tf::TransformBroadcaster tfBroadcaster;
  tf::StampedTransform aftMappedTrans;
  aftMappedTrans.frame_id_ = "/camera_init";
  aftMappedTrans.child_frame_id_ = "/aft_mapped";

  std::vector<int> pointSearchInd;
  std::vector<float> pointSearchSqDis;

  PointType pointOri, pointSel, pointProj, coeff;

  cv::Mat matA0(5, 3, CV_32F, cv::Scalar::all(0));
  cv::Mat matB0(5, 1, CV_32F, cv::Scalar::all(-1));
  cv::Mat matX0(3, 1, CV_32F, cv::Scalar::all(0));

  cv::Mat matA1(3, 3, CV_32F, cv::Scalar::all(0));
  cv::Mat matD1(1, 3, CV_32F, cv::Scalar::all(0));
  cv::Mat matV1(3, 3, CV_32F, cv::Scalar::all(0));

  bool isDegenerate = false;
  cv::Mat matP(6, 6, CV_32F, cv::Scalar::all(0));

  //创建VoxelGrid滤波器（体素栅格滤波器）
  pcl::VoxelGrid<PointType> downSizeFilterCorner;
  //设置体素大小
  downSizeFilterCorner.setLeafSize(0.2, 0.2, 0.2);

  pcl::VoxelGrid<PointType> downSizeFilterSurf;
  downSizeFilterSurf.setLeafSize(0.4, 0.4, 0.4);

  pcl::VoxelGrid<PointType> downSizeFilterMap;
  downSizeFilterMap.setLeafSize(0.6, 0.6, 0.6);
  
  //指针初始化
  for (int i = 0; i < laserCloudNum; i++) {
    laserCloudCornerArray[i].reset(new pcl::PointCloud<PointType>());
    laserCloudSurfArray[i].reset(new pcl::PointCloud<PointType>());
    laserCloudCornerArray2[i].reset(new pcl::PointCloud<PointType>());
    laserCloudSurfArray2[i].reset(new pcl::PointCloud<PointType>());
  }

  int frameCount = stackFrameNum - 1;   //0     stackFrameNum = 1 这个改成10才是论文中的1Hz频率
  int mapFrameCount = mapFrameNum - 1;  //4     mapFrameNum = 5
  ros::Rate rate(100);
  bool status = ros::ok();

接收特征点的回调函数

下面这三个回调函数的作用和代码结构都类似，都是接收laserOdometry发布的话题，分别接收了less edge pointless planar point、full cloud point。

对于接收到点云之后都是如下操作：

• 记录时间戳
• 保存到相应变量中
• 将接收标志设置为true

//接收边沿点
void laserCloudCornerLastHandler(const sensor_msgs::PointCloud2ConstPtr& laserCloudCornerLast2)
{
  timeLaserCloudCornerLast = laserCloudCornerLast2->header.stamp.toSec();

  laserCloudCornerLast->clear();
  pcl::fromROSMsg(*laserCloudCornerLast2, *laserCloudCornerLast);

  newLaserCloudCornerLast = true;
}

//接收平面点
void laserCloudSurfLastHandler(const sensor_msgs::PointCloud2ConstPtr& laserCloudSurfLast2)
{
  timeLaserCloudSurfLast = laserCloudSurfLast2->header.stamp.toSec();

  laserCloudSurfLast->clear();
  pcl::fromROSMsg(*laserCloudSurfLast2, *laserCloudSurfLast);

  newLaserCloudSurfLast = true;
}

//接收点云全部点
void laserCloudFullResHandler(const sensor_msgs::PointCloud2ConstPtr& laserCloudFullRes2)
{
  timeLaserCloudFullRes = laserCloudFullRes2->header.stamp.toSec();

  laserCloudFullRes->clear();
  pcl::fromROSMsg(*laserCloudFullRes2, *laserCloudFullRes);

  newLaserCloudFullRes = true;
}

接收IMU原始数据/imu_data的消息
这个回调函数主要是接收了IMU原始数据话题，更新最新的IMU数据指针imuPointerLast，记录下imu的时间戳，然后这里使用了roll和pitch两个角。

//接收IMU信息，只使用了翻滚角和俯仰角
void imuHandler(const sensor_msgs::Imu::ConstPtr& imuIn)
{
  double roll, pitch, yaw;
  tf::Quaternion orientation;
  tf::quaternionMsgToTF(imuIn->orientation, orientation);
  tf::Matrix3x3(orientation).getRPY(roll, pitch, yaw);

  imuPointerLast = (imuPointerLast + 1) % imuQueLength;

  imuTime[imuPointerLast] = imuIn->header.stamp.toSec();
  imuRoll[imuPointerLast] = roll;
  imuPitch[imuPointerLast] = pitch;
}

接收laserOdometry计算得到的位姿变换

接收laserOdometry模块计算出的当前帧相end相对于初始帧init的坐标变换，并将其保存在transformSum变量中。

//接收旋转平移信息
void laserOdometryHandler(const nav_msgs::Odometry::ConstPtr& laserOdometry)
{
  timeLaserOdometry = laserOdometry->header.stamp.toSec();

  double roll, pitch, yaw;
  //四元数转换为欧拉角
  geometry_msgs::Quaternion geoQuat = laserOdometry->pose.pose.orientation;
  tf::Matrix3x3(tf::Quaternion(geoQuat.z, -geoQuat.x, -geoQuat.y, geoQuat.w)).getRPY(roll, pitch, yaw);

  transformSum[0] = -pitch;
  transformSum[1] = -yaw;
  transformSum[2] = roll;

  transformSum[3] = laserOdometry->pose.pose.position.x;
  transformSum[4] = laserOdometry->pose.pose.position.y;
  transformSum[5] = laserOdometry->pose.pose.position.z;

  newLaserOdometry = true;
}

三、求解初始猜测–transformAssociateToMap()

1.求解位移增量
"transformBefMapped - transformSum"的含义是上一帧相对于初始帧的位移量 与 当前帧相对于初始帧的位移量 的差值，得到的结果是初始帧init坐标系下的位移增量$t_{init}^{start-end}$。

然后将其变换到end时刻：
$$\begin{gathered} t_{init}^{start-end}=R_{end\_init}\ast t_{init}^{start-end}=R_{init\_end}^{-1}\ast t_{init}^{start-end} \\ {R}_{init\_end}^{-1}=R_{ZXY}^{-1}=R_{-rz}{R}_{-rx}{R}_{-ry} \end{gathered}$$
对应于下面代码中所示的变换。

2.求解旋转部分的初始猜测
现在这里的变量含义分别表示为：

• transformSum：当前帧相对于初始帧的变换$R_{init\_end}$
• transformBefMapped：上一帧相对于初始帧的变换$R_{init\_start}$
• transformAftMapped：上一帧优化后的相对于初始帧的变换，也可以理解为上一帧相对于地图坐标系的变换$R_{map\_start}$
• transformTobeMapped：当前帧相对于初始帧的初始猜测，也可以理解为当前帧相对于地图坐标系的变换${\tilde{R}}_{map\_end}$

那么有如下坐标变换关系：
$${\tilde{R}}_{map\_end}=R_{map\_start}\ast R_{init\_start}^{-1}\ast R_{init\_end}=R_{ZXY}\ast R_{ZXY}^{-1}\ast R_{ZXY}$$

这里的计算公式与laserOdometry模块中的IMU修正部分完全一样：
R ~ m a p _ e n d = [ c a c y c a c z + s a c x s a c y s a c z c a c y s a c z + s a c x s a c y c a c z c a c x s a c y c a c x s a c z c a c x c a c z − s a c x − s a c y c a c z + s a c x c a c y s a c z s a c y s a c z + s a c x c a c y c a c z c a c x c a c y ] \tilde R_{map\_end}=\left[ \begin{matrix} cacycacz+sacxsacysacz& cacysacz+sacxsacycacz& cacxsacy\\ cacxsacz& cacxcacz& -sacx\\ -sacycacz+sacxcacysacz& sacysacz+sacxcacycacz& cacxcacy\\ \end{matrix} \right] R~map_end​= ​cacycacz+sacxsacysaczcacxsacz−sacycacz+sacxcacysacz​cacysacz+sacxsacycaczcacxcaczsacysacz+sacxcacycacz​cacxsacy−sacxcacxcacy​ ​
R m a p _ s t a r t = [ c b c y c b c z + s b c x s b c y s b c z c b c y s b c z + s b c x s b c y c b c z c b c x s b c y c b c x s b c z c b c x c b c z − s b c x − s b c y c b c z + s b c x c b c y s b c z s b c y s b c z + s b c x c b c y c b c z c b c x c b c y ] R_{map\_start}=\left[ \begin{matrix} cbcycbcz+sbcxsbcysbcz& cbcysbcz+sbcxsbcycbcz& cbcxsbcy\\ cbcxsbcz& cbcxcbcz& -sbcx\\ -sbcycbcz+sbcxcbcysbcz& sbcysbcz+sbcxcbcycbcz& cbcxcbcy\\ \end{matrix} \right] Rmap_start​= ​cbcycbcz+sbcxsbcysbczcbcxsbcz−sbcycbcz+sbcxcbcysbcz​cbcysbcz+sbcxsbcycbczcbcxcbczsbcysbcz+sbcxcbcycbcz​cbcxsbcy−sbcxcbcxcbcy​ ​
R i n i t _ s t a r t − 1 = [ c b l y c b l z − s b l x s b l y s b l z − c b l x s b l z s b l y c b l z + s b l x c b l y s b l z − c b l y s b l z + s b l x s b l y c b l z c b l x c b l z s b l y s b l z − s b l x c b l y c b l z − c b l x s b l y s b l x c b l x c b l y ] R_{init\_start}^{-1}=\left[ \begin{matrix} cblycblz-sblxsblysblz& -cblxsblz& sblycblz+sblxcblysblz\\ -cblysblz+sblxsblycblz& cblxcblz& sblysblz-sblxcblycblz\\ -cblxsbly& sblx& cblxcbly\\ \end{matrix} \right] Rinit_start−1​= ​cblycblz−sblxsblysblz−cblysblz+sblxsblycblz−cblxsbly​−cblxsblzcblxcblzsblx​sblycblz+sblxcblysblzsblysblz−sblxcblycblzcblxcbly​ ​
R i n i t _ e n d = [ c a l y c a l z + s a l x s a l y s a l z c a l y s a l z + s a l x s a l y c a l z c a l x s a l y c a l x s a l z c a l x c a l z − s a l x − s a l y c a l z + s a l x c a l y s a l z s a l y s a l z + s a l x c a l y c a l z c a l x c a l y ] R_{init\_end}=\left[ \begin{matrix} calycalz+salxsalysalz& calysalz+salxsalycalz& calxsaly\\ calxsalz& calxcalz& -salx\\ -salycalz+salxcalysalz& salysalz+salxcalycalz& calxcaly\\ \end{matrix} \right] Rinit_end​= ​calycalz+salxsalysalzcalxsalz−salycalz+salxcalysalz​calysalz+salxsalycalzcalxcalzsalysalz+salxcalycalz​calxsaly−salxcalxcaly​ ​

然后使用对应位置的值相等，就得到了修正后的累计变换acx、acy、acz，计算如下：
$$\begin{gathered} acx=-arcsin(R_{2,3})=-arcsin(-sbcx\ast (salx\ast sblx+calx\ast caly\ast cblx\ast cbly+calx\ast cblx\ast saly\ast sbly)-cbcx\ast cbcz\ast (calx\ast saly\ast (cbly\ast sblz-cblz\ast sblx\ast sbly)-calx\ast caly\ast (sbly\ast sblz+cbly\ast cblz\ast sblx)+cblx\ast cblz\ast salx)-cbcx\ast sbcz\ast (calx\ast caly\ast (cblz\ast sbly-cbly\ast sblx\ast sblz)-calx\ast saly\ast (cbly\ast cblz+sblx\ast sbly\ast sblz)+cblx\ast salx\ast sblz)) \\ acy=arctan(R_{1,3}/R_{3,3}) \\ acz=arctan(R_{2,1}/R_{2,2}) \end{gathered}$$

3.将位移增量转换到map坐标系
$$\begin{gathered} t_{map}^{increment}={\tilde{R}}_{map\_end}\ast t_{end}^{increment} \\ {\tilde{R}}_{map\_end}=R_{ZXY}=R_y{R}_x{R}_z \end{gathered}$$

4.求解平移部分的初始猜测
这里注意一点：上面求出来的增量使用的事start时刻的累积位移减去end时刻的累计位移，所以这里在求解时也是减号，如下：
$${\tilde{t}}_{map\_end}=t_{map\_start}+t_{map}^{end-start}=t_{map\_start}-t_{map}^{start-end}$$

//基于匀速模型，根据上次微调的结果和odometry这次与上次计算的结果，猜测一个新的世界坐标系的转换矩阵transformTobeMapped
// 得到T_map_end的初始猜测transformTobeMapped
void transformAssociateToMap()
{
  // 这个写的很好：https://zhuanlan.zhihu.com/p/159525107
        
  // 这里用到的旋转矩阵：R_end_init = R_init_end^{-1} = R_ZXY^{-1} = R_-rz * R_-rx * R_-ry
  // 这里的运算把括号拆开看：transformIncre = t_end^{start-end} = R_end_init * t_init^{start-end}
  //                                    = R_end_init * (t_init_start - t_init_end)
    
  //绕y轴旋转 -ry
  float x1 = cos(transformSum[1]) * (transformBefMapped[3] - transformSum[3]) 
           - sin(transformSum[1]) * (transformBefMapped[5] - transformSum[5]);
  float y1 = transformBefMapped[4] - transformSum[4];
  float z1 = sin(transformSum[1]) * (transformBefMapped[3] - transformSum[3]) 
           + cos(transformSum[1]) * (transformBefMapped[5] - transformSum[5]);
  //绕x轴旋转 -rx
  float x2 = x1;
  float y2 = cos(transformSum[0]) * y1 + sin(transformSum[0]) * z1;
  float z2 = -sin(transformSum[0]) * y1 + cos(transformSum[0]) * z1;

  //绕z轴旋转 -rz
  //平移增量
  transformIncre[3] = cos(transformSum[2]) * x2 + sin(transformSum[2]) * y2;
  transformIncre[4] = -sin(transformSum[2]) * x2 + cos(transformSum[2]) * y2;
  transformIncre[5] = z2;

  // T_init_end
  float sbcx = sin(transformSum[0]);
  float cbcx = cos(transformSum[0]);
  float sbcy = sin(transformSum[1]);
  float cbcy = cos(transformSum[1]);
  float sbcz = sin(transformSum[2]);
  float cbcz = cos(transformSum[2]);

  // T_init_start
  float sblx = sin(transformBefMapped[0]);
  float cblx = cos(transformBefMapped[0]);
  float sbly = sin(transformBefMapped[1]);
  float cbly = cos(transformBefMapped[1]);
  float sblz = sin(transformBefMapped[2]);
  float cblz = cos(transformBefMapped[2]);

  //transformAftMapped是上一次构图经过mapping微调后的转换矩阵，
  //可以理解为上一次的构图帧最终解算的位姿 T_map_start
  float salx = sin(transformAftMapped[0]);
  float calx = cos(transformAftMapped[0]);
  float saly = sin(transformAftMapped[1]);
  float caly = cos(transformAftMapped[1]);
  float salz = sin(transformAftMapped[2]);
  float calz = cos(transformAftMapped[2]);
  
  // R_transformTobeMapped
  // = （初始猜测）R_map_end 
  // = R_map_start * (R_init_start)^{-1} * R_init_end
  // = R_transformAftMapped * (R_transformBefMapped)^{-1} * R_transformSum
  float srx = -sbcx*(salx*sblx + calx*cblx*salz*sblz + calx*calz*cblx*cblz)
            - cbcx*sbcy*(calx*calz*(cbly*sblz - cblz*sblx*sbly)
            - calx*salz*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sbly)
            - cbcx*cbcy*(calx*salz*(cblz*sbly - cbly*sblx*sblz) 
            - calx*calz*(sbly*sblz + cbly*cblz*sblx) + cblx*cbly*salx);
  transformTobeMapped[0] = -asin(srx);

  float srycrx = sbcx*(cblx*cblz*(caly*salz - calz*salx*saly)
               - cblx*sblz*(caly*calz + salx*saly*salz) + calx*saly*sblx)
               - cbcx*cbcy*((caly*calz + salx*saly*salz)*(cblz*sbly - cbly*sblx*sblz)
               + (caly*salz - calz*salx*saly)*(sbly*sblz + cbly*cblz*sblx) - calx*cblx*cbly*saly)
               + cbcx*sbcy*((caly*calz + salx*saly*salz)*(cbly*cblz + sblx*sbly*sblz)
               + (caly*salz - calz*salx*saly)*(cbly*sblz - cblz*sblx*sbly) + calx*cblx*saly*sbly);
  float crycrx = sbcx*(cblx*sblz*(calz*saly - caly*salx*salz)
               - cblx*cblz*(saly*salz + caly*calz*salx) + calx*caly*sblx)
               + cbcx*cbcy*((saly*salz + caly*calz*salx)*(sbly*sblz + cbly*cblz*sblx)
               + (calz*saly - caly*salx*salz)*(cblz*sbly - cbly*sblx*sblz) + calx*caly*cblx*cbly)
               - cbcx*sbcy*((saly*salz + caly*calz*salx)*(cbly*sblz - cblz*sblx*sbly)
               + (calz*saly - caly*salx*salz)*(cbly*cblz + sblx*sbly*sblz) - calx*caly*cblx*sbly);
  transformTobeMapped[1] = atan2(srycrx / cos(transformTobeMapped[0]), 
                                 crycrx / cos(transformTobeMapped[0]));
  
  float srzcrx = (cbcz*sbcy - cbcy*sbcx*sbcz)*(calx*salz*(cblz*sbly - cbly*sblx*sblz)
               - calx*calz*(sbly*sblz + cbly*cblz*sblx) + cblx*cbly*salx)
               - (cbcy*cbcz + sbcx*sbcy*sbcz)*(calx*calz*(cbly*sblz - cblz*sblx*sbly)
               - calx*salz*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sbly)
               + cbcx*sbcz*(salx*sblx + calx*cblx*salz*sblz + calx*calz*cblx*cblz);
  float crzcrx = (cbcy*sbcz - cbcz*sbcx*sbcy)*(calx*calz*(cbly*sblz - cblz*sblx*sbly)
               - calx*salz*(cbly*cblz + sblx*sbly*sblz) + cblx*salx*sbly)
               - (sbcy*sbcz + cbcy*cbcz*sbcx)*(calx*salz*(cblz*sbly - cbly*sblx*sblz)
               - calx*calz*(sbly*sblz + cbly*cblz*sblx) + cblx*cbly*salx)
               + cbcx*cbcz*(salx*sblx + calx*cblx*salz*sblz + calx*calz*cblx*cblz);
  transformTobeMapped[2] = atan2(srzcrx / cos(transformTobeMapped[0]), 
                                 crzcrx / cos(transformTobeMapped[0]));

  //这样就得到了一个世界系到当前构图帧的不错的初始姿态，存入transformTobeMapped中，用作迭代匹配的初值
  
  // 转换到map坐标系
  // 这里用到的旋转矩阵：R_map_end = R_ZXY = R_rz * R_rx * R_ry
  // 把位移增量转换到map坐标系下：t_map^{start-end} = R_map_end * t_end^{start-end}
  //绕z轴旋转 +rz
  x1 = cos(transformTobeMapped[2]) * transformIncre[3] - sin(transformTobeMapped[2]) * transformIncre[4];
  y1 = sin(transformTobeMapped[2]) * transformIncre[3] + cos(transformTobeMapped[2]) * transformIncre[4];
  z1 = transformIncre[5];

  //绕x轴旋转 +rx
  x2 = x1;
  y2 = cos(transformTobeMapped[0]) * y1 - sin(transformTobeMapped[0]) * z1;
  z2 = sin(transformTobeMapped[0]) * y1 + cos(transformTobeMapped[0]) * z1;

  //绕y轴旋转 +ry
  transformTobeMapped[3] = transformAftMapped[3] 
                         - (cos(transformTobeMapped[1]) * x2 + sin(transformTobeMapped[1]) * z2);
  transformTobeMapped[4] = transformAftMapped[4] - y2;
  transformTobeMapped[5] = transformAftMapped[5] 
                         - (-sin(transformTobeMapped[1]) * x2 + cos(transformTobeMapped[1]) * z2);
  // t_map_end = t_map_start - t_map^{start-end}
}

三、将接收到的点转换到地图坐标系下

这一部分主要的功能就是判断一下时间戳和是否接受到该帧的特征点，如果接收到了的好，就根据初始猜测，将接收到的点从end时刻坐标系变换到map坐标系下，主要函数就是pointAssociateToMap()函数

  while (status) {
    ros::spinOnce();

    if (newLaserCloudCornerLast && newLaserCloudSurfLast && newLaserCloudFullRes && newLaserOdometry &&
        fabs(timeLaserCloudCornerLast - timeLaserOdometry) < 0.005 &&
        fabs(timeLaserCloudSurfLast - timeLaserOdometry) < 0.005 &&
        fabs(timeLaserCloudFullRes - timeLaserOdometry) < 0.005) {
      newLaserCloudCornerLast = false;
      newLaserCloudSurfLast = false;
      newLaserCloudFullRes = false;
      newLaserOdometry = false;

      frameCount++;
      //控制跳帧数，>=这里实际并没有跳帧，只取>或者增大stackFrameNum才能实现相应的跳帧处理
      if (frameCount >= stackFrameNum) {
        //获取T_map_end的初始猜测
        transformAssociateToMap();

        //将最新接收到的平面点和边沿点进行旋转平移转换到地图坐标系map下
        int laserCloudCornerLastNum = laserCloudCornerLast->points.size();
        for (int i = 0; i < laserCloudCornerLastNum; i++) {
          pointAssociateToMap(&laserCloudCornerLast->points[i], &pointSel);
          laserCloudCornerStack2->push_back(pointSel);
        }

        int laserCloudSurfLastNum = laserCloudSurfLast->points.size();
        for (int i = 0; i < laserCloudSurfLastNum; i++) {
          pointAssociateToMap(&laserCloudSurfLast->points[i], &pointSel);
          laserCloudSurfStack2->push_back(pointSel);
        }
      }

pointAssociateToMap()函数
输入的pi是end时刻坐标系下的点，这个变换过程如下式：
$$p_{map}={\tilde{R}}_{map\_end}\ast p_{end}+t_{map\_end}=R_y{R}_x{R}_z\ast p_{end}+t_{map\_end}$$

//根据调整计算后的转移矩阵，将点注册到全局世界坐标系下
void pointAssociateToMap(PointType const * const pi, PointType * const po)
{
  //绕z轴旋转（transformTobeMapped[2]）
  float x1 = cos(transformTobeMapped[2]) * pi->x
           - sin(transformTobeMapped[2]) * pi->y;
  float y1 = sin(transformTobeMapped[2]) * pi->x
           + cos(transformTobeMapped[2]) * pi->y;
  float z1 = pi->z;

  //绕x轴旋转（transformTobeMapped[0]）
  float x2 = x1;
  float y2 = cos(transformTobeMapped[0]) * y1 - sin(transformTobeMapped[0]) * z1;
  float z2 = sin(transformTobeMapped[0]) * y1 + cos(transformTobeMapped[0]) * z1;

  //绕y轴旋转（transformTobeMapped[1]），再平移
  po->x = cos(transformTobeMapped[1]) * x2 + sin(transformTobeMapped[1]) * z2
        + transformTobeMapped[3];
  po->y = y2 + transformTobeMapped[4];
  po->z = -sin(transformTobeMapped[1]) * x2 + cos(transformTobeMapped[1]) * z2
        + transformTobeMapped[5];
  po->intensity = pi->intensity;
}

四、维护局部地图

首先，前面求解了一个在y方向上10米高位置的点在世界坐标系下的坐标，这个主要是为了后面帮助判断周围选定的周围点云集合S`中的cube是否在激光雷达的视域内，可以先不用管它，之后我们再讲。

下面先声明一些局部地图中使用到的变量：

• laserCloudCornerArray：存放edge point的总地图，按照论文的话就是所有cube的总集合，一共有laserCloudNum=211121个cube，一个cube尺寸为50x50x50米
• laserCloudSurfArray：存放planar point的总地图，按照论文的话就是所有cube的总集合，一共有laserCloudNum=211121个cube，一个cube尺寸为50x50x50米
• laserCloudWidth：宽度方向cube数量//21
• laserCloudHeight：高度方向cube数量//11
• laserCloudDepth：深度方向cube数量//21
• laserCloudNum：总cube数量 = laserCloudWidth * laserCloudHeight * laserCloudDepth;//21x11x21
• laserCloudCenWidth：地图中心点在宽度方向的偏移量//(21+1)/2
• laserCloudCenHeight：地图中心点在高度方向的偏移量//(11+1)/2
• laserCloudCenDepth：地图中心点在深度方向的偏移量//(21+1)/2
• laserCloudSurroundInd：构成周围点云cube集合的索引，对应论文中构成S`的cube的索引
• laserCloudValidInd：构成周围点云cube集合，并且在激光雷达视域范围内的索引
• centerCubeI：机器人位置在地图中宽度方向的cube索引
• centerCubeJ：机器人位置在地图中高度方向的cube索引
• centerCubeK：机器人位置在地图中深度方向的cube索引

下面就是求解机器人位置的cube索引centerCubeI、centerCubeJ、centerCubeK，下图源自：SLAM前端入门框架-A_LOAM源码解析-知乎
然后下面六个while循环，就是循环移位的过程，如果机器人的位置靠近了地图边缘，那就调整地图的中心靠近机器人的位置，比如第一个while循环，意思是如果centerCubeI<3，说明机器人位置处于下边界，表明地图向负方向延伸的可能性比较大，则循环移位，将数组中心点向上边界调整一个单位。

调整后需要满足：

3 < centerCubeI < 18， 3 < centerCubeJ < 8, 3 < centerCubeK < 18

      if (frameCount >= stackFrameNum) {
        frameCount = 0;

        PointType pointOnYAxis;
        pointOnYAxis.x = 0.0;
        pointOnYAxis.y = 10.0;
        pointOnYAxis.z = 0.0;
        //获取y方向上10米高位置的点在世界坐标系下的坐标
        pointAssociateToMap(&pointOnYAxis, &pointOnYAxis);

        //立方体的中点（原点）在世界坐标系下的位置
        //过半取一（以50米进行四舍五入的效果），由于数组下标只能为正数，而地图可能建立在原点前后，因此
        //每一维偏移一个laserCloudCenWidth（该值会动态调整，以使得数组利用最大化，初始值为该维数组长度1/2）的量
        int centerCubeI = int((transformTobeMapped[3] + 25.0) / 50.0) + laserCloudCenWidth;
        int centerCubeJ = int((transformTobeMapped[4] + 25.0) / 50.0) + laserCloudCenHeight;
        int centerCubeK = int((transformTobeMapped[5] + 25.0) / 50.0) + laserCloudCenDepth;

        //由于计算机求余是向零取整，为了不使（-50.0,50.0）求余后都向零偏移，当被求余数为负数时求余结果统一向左偏移一个单位，也即减一
        if (transformTobeMapped[3] + 25.0 < 0) centerCubeI--;
        if (transformTobeMapped[4] + 25.0 < 0) centerCubeJ--;
        if (transformTobeMapped[5] + 25.0 < 0) centerCubeK--;

        //调整之后取值范围:3 < centerCubeI < 18， 3 < centerCubeJ < 8, 3 < centerCubeK < 18
        //如果处于下边界，表明地图向负方向延伸的可能性比较大，则循环移位，将数组中心点向上边界调整一个单位
        while (centerCubeI < 3) {
          for (int j = 0; j < laserCloudHeight; j++) {
            for (int k = 0; k < laserCloudDepth; k++) {//实现一次循环移位效果
              int i = laserCloudWidth - 1;
              //指针赋值，保存最后一个指针位置
              pcl::PointCloud<PointType>::Ptr laserCloudCubeCornerPointer =
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];//that's [i + 21 * j + 231 * k]
              pcl::PointCloud<PointType>::Ptr laserCloudCubeSurfPointer =
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              //循环移位，I维度上依次后移
              for (; i >= 1; i--) {
                laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudCornerArray[i - 1 + laserCloudWidth*j + laserCloudWidth * laserCloudHeight * k];
                laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudSurfArray[i - 1 + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              }
              //将开始点赋值为最后一个点
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeCornerPointer;
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeSurfPointer;
              laserCloudCubeCornerPointer->clear();
              laserCloudCubeSurfPointer->clear();
            }
          }

          centerCubeI++;
          laserCloudCenWidth++;
        }

        //如果处于上边界，表明地图向正方向延伸的可能性比较大，则循环移位，将数组中心点向下边界调整一个单位
        while (centerCubeI >= laserCloudWidth - 3) {//18
          for (int j = 0; j < laserCloudHeight; j++) {
            for (int k = 0; k < laserCloudDepth; k++) {
              int i = 0;
              pcl::PointCloud<PointType>::Ptr laserCloudCubeCornerPointer =
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              pcl::PointCloud<PointType>::Ptr laserCloudCubeSurfPointer =
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              //I维度上依次前移
              for (; i < laserCloudWidth - 1; i++) {
                laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudCornerArray[i + 1 + laserCloudWidth*j + laserCloudWidth * laserCloudHeight * k];
                laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudSurfArray[i + 1 + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              }
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeCornerPointer;
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeSurfPointer;
              laserCloudCubeCornerPointer->clear();
              laserCloudCubeSurfPointer->clear();
            }
          }

          centerCubeI--;
          laserCloudCenWidth--;
        }

        while (centerCubeJ < 3) {
          for (int i = 0; i < laserCloudWidth; i++) {
            for (int k = 0; k < laserCloudDepth; k++) {
              int j = laserCloudHeight - 1;
              pcl::PointCloud<PointType>::Ptr laserCloudCubeCornerPointer =
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              pcl::PointCloud<PointType>::Ptr laserCloudCubeSurfPointer =
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              //J维度上，依次后移
              for (; j >= 1; j--) {
                laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudCornerArray[i + laserCloudWidth*(j - 1) + laserCloudWidth * laserCloudHeight*k];
                laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudSurfArray[i + laserCloudWidth * (j - 1) + laserCloudWidth * laserCloudHeight*k];
              }
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeCornerPointer;
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeSurfPointer;
              laserCloudCubeCornerPointer->clear();
              laserCloudCubeSurfPointer->clear();
            }
          }
 
          centerCubeJ++;
          laserCloudCenHeight++;
        } 

        while (centerCubeJ >= laserCloudHeight - 3) {
          for (int i = 0; i < laserCloudWidth; i++) {
            for (int k = 0; k < laserCloudDepth; k++) {
              int j = 0;
              pcl::PointCloud<PointType>::Ptr laserCloudCubeCornerPointer =
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              pcl::PointCloud<PointType>::Ptr laserCloudCubeSurfPointer =
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              //J维度上一次前移
              for (; j < laserCloudHeight - 1; j++) {
                laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudCornerArray[i + laserCloudWidth*(j + 1) + laserCloudWidth * laserCloudHeight*k];
                laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudSurfArray[i + laserCloudWidth * (j + 1) + laserCloudWidth * laserCloudHeight*k];
              }
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeCornerPointer;
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeSurfPointer;
              laserCloudCubeCornerPointer->clear();
              laserCloudCubeSurfPointer->clear();
            }
          }

          centerCubeJ--;
          laserCloudCenHeight--;
        }

        while (centerCubeK < 3) {
          for (int i = 0; i < laserCloudWidth; i++) {
            for (int j = 0; j < laserCloudHeight; j++) {
              int k = laserCloudDepth - 1;
              pcl::PointCloud<PointType>::Ptr laserCloudCubeCornerPointer =
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              pcl::PointCloud<PointType>::Ptr laserCloudCubeSurfPointer =
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              //K维度上依次后移
              for (; k >= 1; k--) {
                laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudCornerArray[i + laserCloudWidth*j + laserCloudWidth * laserCloudHeight*(k - 1)];
                laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight*(k - 1)];
              }
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeCornerPointer;
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeSurfPointer;
              laserCloudCubeCornerPointer->clear();
              laserCloudCubeSurfPointer->clear();
            }
          }

          centerCubeK++;
          laserCloudCenDepth++;
        }
      
        while (centerCubeK >= laserCloudDepth - 3) {
          for (int i = 0; i < laserCloudWidth; i++) {
            for (int j = 0; j < laserCloudHeight; j++) {
              int k = 0;
              pcl::PointCloud<PointType>::Ptr laserCloudCubeCornerPointer =
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              pcl::PointCloud<PointType>::Ptr laserCloudCubeSurfPointer =
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k];
              //K维度上依次前移
              for (; k < laserCloudDepth - 1; k++) {
                laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudCornerArray[i + laserCloudWidth*j + laserCloudWidth * laserCloudHeight*(k + 1)];
                laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] =
                laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight*(k + 1)];
              }
              laserCloudCornerArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeCornerPointer;
              laserCloudSurfArray[i + laserCloudWidth * j + laserCloudWidth * laserCloudHeight * k] = 
              laserCloudCubeSurfPointer;
              laserCloudCubeCornerPointer->clear();
              laserCloudCubeSurfPointer->clear();
            }
          }

          centerCubeK--;
          laserCloudCenDepth--;
        }

五、构建周围点云地图S`

这一部分对应于论文中下面这一段：

以机器人当前位置所处的cube为中心，取宽度方向5个、深度方向5个、高度方向5个（前后250米范围内，总共500米范围），三个维度总共125个cube，然后在这125个cube里面进一步筛选在视域范围内的cube。

筛选方法如下：

1. 先将周围125个cube的每一个cube索引换算成在世界坐标系下的坐标(以米为单位)
2. 取周围125个cube的每一个cube的上下左右八个顶点坐标
3. 求原点到顶点距离的平方和机器人上方10m一个点pointOnYAxis到顶点距离的平方
4. 应用余弦定理求解角度，如果在(30,150)范围内则认为在视域内，图示如下

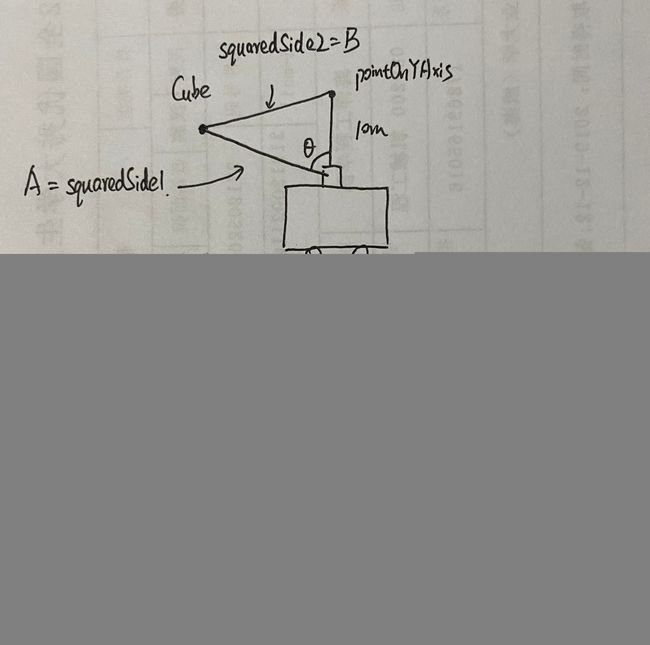
如果check1<0并且check2>0，就说明图示中的θ角在30度到150度之间，判定为在激光雷达视域范围内。

如果某个cube在视域内，就将该cube的索引保存到laserCloudValidInd[]数组中；然后不管是不是在视域内，都将cube的索引保存到laserCloudSurroundInd[]数组中

最后再通过一个for循环，使用在视域范围内的cube构建周围点云S`，代码中为laserCloudCornerFromMap和laserCloudSurfFromMap点云

        //下面这个三层for循环用来寻找构成局部点云集合S`的cube
        int laserCloudValidNum = 0;     // 局部地图有效(在视野范围内)cube数量
        int laserCloudSurroundNum = 0;  // 局部地图所有cube数量
        //在每一维附近5个cube(前2个，后2个，中间1个)里进行查找（前后250米范围内，总共500米范围），三个维度总共125个cube
        //在这125个cube里面进一步筛选在视域范围内的cube
        for (int i = centerCubeI - 2; i <= centerCubeI + 2; i++) {
          for (int j = centerCubeJ - 2; j <= centerCubeJ + 2; j++) {
            for (int k = centerCubeK - 2; k <= centerCubeK + 2; k++) {
              if (i >= 0 && i < laserCloudWidth && 
                  j >= 0 && j < laserCloudHeight && 
                  k >= 0 && k < laserCloudDepth) {//如果索引合法

                //换算成实际比例，在世界坐标系下的坐标
                float centerX = 50.0 * (i - laserCloudCenWidth);
                float centerY = 50.0 * (j - laserCloudCenHeight);
                float centerZ = 50.0 * (k - laserCloudCenDepth);

                //下面的代码是用来判断周围点云集合S`的cube是否在雷达的视线范围内
                bool isInLaserFOV = false;
                for (int ii = -1; ii <= 1; ii += 2) {
                  for (int jj = -1; jj <= 1; jj += 2) {
                    for (int kk = -1; kk <= 1; kk += 2) {
                      //周围点云S`中的cube的上下左右八个顶点坐标
                      float cornerX = centerX + 25.0 * ii;
                      float cornerY = centerY + 25.0 * jj;
                      float cornerZ = centerZ + 25.0 * kk;

                      //原点到顶点距离的平方
                      float squaredSide1 = (transformTobeMapped[3] - cornerX) 
                                         * (transformTobeMapped[3] - cornerX) 
                                         + (transformTobeMapped[4] - cornerY) 
                                         * (transformTobeMapped[4] - cornerY)
                                         + (transformTobeMapped[5] - cornerZ) 
                                         * (transformTobeMapped[5] - cornerZ);

                      //pointOnYAxis到顶点距离的平方
                      float squaredSide2 = (pointOnYAxis.x - cornerX) * (pointOnYAxis.x - cornerX) 
                                         + (pointOnYAxis.y - cornerY) * (pointOnYAxis.y - cornerY)
                                         + (pointOnYAxis.z - cornerZ) * (pointOnYAxis.z - cornerZ);

                      //用了余弦定理，check1其实是：机器人原点位置与cube中点的连线 与 机器人上方10m线段 的夹角 的余弦 - cos30
                      //如果check1<0说明：这个夹角大于30度，在视野范围内
                      float check1 = 100.0 + squaredSide1 - squaredSide2
                                   - 10.0 * sqrt(3.0) * sqrt(squaredSide1);

                      //check2其实是：机器人原点位置与cube中点的连线 与 机器人上方10m线段 的夹角 的余弦 - cos150
                      //如果check2>0说明：这个夹角小于150度，在视野范围内
                      float check2 = 100.0 + squaredSide1 - squaredSide2
                                   + 10.0 * sqrt(3.0) * sqrt(squaredSide1);

                      //其实就是激光雷达的视野(-30,30)
                      if (check1 < 0 && check2 > 0) {
                        isInLaserFOV = true;
                      }
                    }
                  }
                }

                //记住视域范围内的cube索引，匹配用
                if (isInLaserFOV) {
                  laserCloudValidInd[laserCloudValidNum] = i + laserCloudWidth * j 
                                                       + laserCloudWidth * laserCloudHeight * k;
                  laserCloudValidNum++;
                }
                //记住附近所有cube的索引，显示用
                laserCloudSurroundInd[laserCloudSurroundNum] = i + laserCloudWidth * j 
                                                             + laserCloudWidth * laserCloudHeight * k;
                laserCloudSurroundNum++;
              }
            }
          }
        }

        laserCloudCornerFromMap->clear();
        laserCloudSurfFromMap->clear();
        //构建特征点地图，查找匹配使用，对应于论文中S`的部分
        for (int i = 0; i < laserCloudValidNum; i++) {
          *laserCloudCornerFromMap += *laserCloudCornerArray[laserCloudValidInd[i]];
          *laserCloudSurfFromMap += *laserCloudSurfArray[laserCloudValidInd[i]];
        }

六、特征匹配

首先将点云又变回局部坐标系，也就是里程计坐标系下的end时刻，个人没看懂这个操作有什么意义，前面变到map坐标系中也没进行什么操作。

对视域范围内的周围点云S`进行降采样操作，以减少运算量，然后如果周围点云中edge point数量大于10并且planar point数量大于100，则开始进行特征匹配。

6.1 edge point匹配

用S`构造KD-tree，搜索与待匹配点最近的5个点，求这5个点的均值保存在cx、cy、cz中，求这5个点构成的协方差矩阵，保存在matA1矩阵中，然后对matA1进行特征值分解。

接下来就是判断这五个点是否构成一条直线，按照论文所述，如果三个特征值中，有一个特征值明显大于其他两个，则认为这5个点构成一条直线，且该特征值对应的特征向量为构成直线的方向向量，在代码中当最大特征大于次大特征值3倍以上，则认为构成直线。

在均值点处沿着方向向量，乘以+0.1和-0.1分别构造出该直线上两个点，即代码中的(x1,y1,z1)和(x2,y2,z2)，然后类似于laserOdometry中的方法，求解待匹配点到直线的距离以及垂线向量在xyz轴三个方向的分量保存到coeff中，匹配成功的点放入laserCloudOri中。

        int laserCloudCornerFromMapNum = laserCloudCornerFromMap->points.size();
        int laserCloudSurfFromMapNum = laserCloudSurfFromMap->points.size();

        /***********************************************************************
          此处将特征点转移回local坐标系，是为了voxel grid filter的下采样操作不越
          界？好像不是！后面还会转移回世界坐标系，这里是前面的逆转换，和前面一样
          应无必要，可直接对laserCloudCornerLast和laserCloudSurfLast进行下采样
        ***********************************************************************/
        int laserCloudCornerStackNum2 = laserCloudCornerStack2->points.size();
        for (int i = 0; i < laserCloudCornerStackNum2; i++) {
          pointAssociateTobeMapped(&laserCloudCornerStack2->points[i], &laserCloudCornerStack2->points[i]);
        }

        int laserCloudSurfStackNum2 = laserCloudSurfStack2->points.size();
        for (int i = 0; i < laserCloudSurfStackNum2; i++) {
          pointAssociateTobeMapped(&laserCloudSurfStack2->points[i], &laserCloudSurfStack2->points[i]);
        }

        // 为了减少运算量，对点云进行下采样
        laserCloudCornerStack->clear();
        downSizeFilterCorner.setInputCloud(laserCloudCornerStack2);//设置滤波对象
        downSizeFilterCorner.filter(*laserCloudCornerStack);//执行滤波处理
        int laserCloudCornerStackNum = laserCloudCornerStack->points.size();//获取滤波后体素点尺寸

        laserCloudSurfStack->clear();
        downSizeFilterSurf.setInputCloud(laserCloudSurfStack2);
        downSizeFilterSurf.filter(*laserCloudSurfStack);
        int laserCloudSurfStackNum = laserCloudSurfStack->points.size();

        laserCloudCornerStack2->clear();
        laserCloudSurfStack2->clear();

        //如果点云数量足够大
        if (laserCloudCornerFromMapNum > 10 && laserCloudSurfFromMapNum > 100) {
          kdtreeCornerFromMap->setInputCloud(laserCloudCornerFromMap);//构建kd-tree
          kdtreeSurfFromMap->setInputCloud(laserCloudSurfFromMap);

          for (int iterCount = 0; iterCount < 10; iterCount++) {//最多迭代10次
            laserCloudOri->clear();
            coeffSel->clear();

            for (int i = 0; i < laserCloudCornerStackNum; i++) {
              pointOri = laserCloudCornerStack->points[i];
              //转换回世界坐标系
              pointAssociateToMap(&pointOri, &pointSel);
              kdtreeCornerFromMap->nearestKSearch(pointSel, 5, pointSearchInd, pointSearchSqDis);//寻找最近距离五个点
              
              if (pointSearchSqDis[4] < 1.0) {//5个点中最大距离不超过1才处理
                //将五个最近点的坐标加和求平均
                float cx = 0;
                float cy = 0; 
                float cz = 0;
                for (int j = 0; j < 5; j++) {
                  cx += laserCloudCornerFromMap->points[pointSearchInd[j]].x;
                  cy += laserCloudCornerFromMap->points[pointSearchInd[j]].y;
                  cz += laserCloudCornerFromMap->points[pointSearchInd[j]].z;
                }
                cx /= 5;
                cy /= 5; 
                cz /= 5;

                //求均方差
                float a11 = 0;
                float a12 = 0; 
                float a13 = 0;
                float a22 = 0;
                float a23 = 0; 
                float a33 = 0;
                for (int j = 0; j < 5; j++) {
                  float ax = laserCloudCornerFromMap->points[pointSearchInd[j]].x - cx;
                  float ay = laserCloudCornerFromMap->points[pointSearchInd[j]].y - cy;
                  float az = laserCloudCornerFromMap->points[pointSearchInd[j]].z - cz;

                  a11 += ax * ax;
                  a12 += ax * ay;
                  a13 += ax * az;
                  a22 += ay * ay;
                  a23 += ay * az;
                  a33 += az * az;
                }
                a11 /= 5;
                a12 /= 5; 
                a13 /= 5;
                a22 /= 5;
                a23 /= 5; 
                a33 /= 5;

                //构建协方差矩阵
                matA1.at<float>(0, 0) = a11;
                matA1.at<float>(0, 1) = a12;
                matA1.at<float>(0, 2) = a13;
                matA1.at<float>(1, 0) = a12;
                matA1.at<float>(1, 1) = a22;
                matA1.at<float>(1, 2) = a23;
                matA1.at<float>(2, 0) = a13;
                matA1.at<float>(2, 1) = a23;
                matA1.at<float>(2, 2) = a33;

                //特征值分解
                cv::eigen(matA1, matD1, matV1);

                // 论文中：最大特征值大于次大特征值的3倍认为是线特征
                if (matD1.at<float>(0, 0) > 3 * matD1.at<float>(0, 1)) {//如果最大的特征值大于第二大的特征值三倍以上

                  float x0 = pointSel.x;
                  float y0 = pointSel.y;
                  float z0 = pointSel.z;
                  float x1 = cx + 0.1 * matV1.at<float>(0, 0);
                  float y1 = cy + 0.1 * matV1.at<float>(0, 1);
                  float z1 = cz + 0.1 * matV1.at<float>(0, 2);
                  float x2 = cx - 0.1 * matV1.at<float>(0, 0);
                  float y2 = cy - 0.1 * matV1.at<float>(0, 1);
                  float z2 = cz - 0.1 * matV1.at<float>(0, 2);

                  float a012 = sqrt(((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1))
                             * ((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)) 
                             + ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))
                             * ((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1)) 
                             + ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))
                             * ((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1)));    //OA、OB叉乘的模

                  float l12 = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2) + (z1 - z2)*(z1 - z2));    //AB的模
    
                  //O到AB的垂线的方向向量在三个方向的分量
                  float la = ((y1 - y2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)) 
                           + (z1 - z2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1))) / a012 / l12;

                  float lb = -((x1 - x2)*((x0 - x1)*(y0 - y2) - (x0 - x2)*(y0 - y1)) 
                           - (z1 - z2)*((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))) / a012 / l12;

                  float lc = -((x1 - x2)*((x0 - x1)*(z0 - z2) - (x0 - x2)*(z0 - z1)) 
                           + (y1 - y2)*((y0 - y1)*(z0 - z2) - (y0 - y2)*(z0 - z1))) / a012 / l12;

                  float ld2 = a012 / l12;

                  //unused
                  pointProj = pointSel;
                  pointProj.x -= la * ld2;
                  pointProj.y -= lb * ld2;
                  pointProj.z -= lc * ld2;

                  //权重系数计算
                  float s = 1 - 0.9 * fabs(ld2);

                  coeff.x = s * la;
                  coeff.y = s * lb;
                  coeff.z = s * lc;
                  coeff.intensity = s * ld2;

                  if (s > 0.1) {//距离足够小才使用
                    laserCloudOri->push_back(pointOri);
                    coeffSel->push_back(coeff);
                  }
                }
              }
            }

6.2 planar point匹配

用S`构造KD-tree，搜索与待匹配点最近的5个点，用这5个点构建了一个超定方程组，用来求解平面方程Ax + By +Cz + 1 = 0的ABCD系数，尝试去拟合一个平面。

接下来就是判断这五个点拟合的这个平面好不好，论文中的判断方法是如果有一个特征值远远小于其他两个特征值，那么这个特征值对应的特征向量为平面的法向量，但是在代码中并没有使用这种方式。

代码中的方法是：求解用于拟合的5个点到拟合出的平面的距离，如果有任何一个距离大于0.2米，则认为平面拟合的不好，将不进行匹配；否则，将记录下平面参数和待匹配点到平面的距离保存在coeffSel中，将匹配成功的点保存到laserCloudOri中。

            for (int i = 0; i < laserCloudSurfStackNum; i++) {
              pointOri = laserCloudSurfStack->points[i];
              pointAssociateToMap(&pointOri, &pointSel); 
              kdtreeSurfFromMap->nearestKSearch(pointSel, 5, pointSearchInd, pointSearchSqDis);

              if (pointSearchSqDis[4] < 1.0) {
                // 构建平面方程Ax + By +Cz + 1 = 0
                // 通过构建一个超定方程来求解这个平面方程
                for (int j = 0; j < 5; j++) {
                  matA0.at<float>(j, 0) = laserCloudSurfFromMap->points[pointSearchInd[j]].x;
                  matA0.at<float>(j, 1) = laserCloudSurfFromMap->points[pointSearchInd[j]].y;
                  matA0.at<float>(j, 2) = laserCloudSurfFromMap->points[pointSearchInd[j]].z;
                }
                //求解matA0*matX0=matB0
                cv::solve(matA0, matB0, matX0, cv::DECOMP_QR);

                float pa = matX0.at<float>(0, 0);
                float pb = matX0.at<float>(1, 0);
                float pc = matX0.at<float>(2, 0);
                float pd = 1;
 
                float ps = sqrt(pa * pa + pb * pb + pc * pc);
                pa /= ps;
                pb /= ps;
                pc /= ps;
                pd /= ps;

                bool planeValid = true;
                // 点如果距离平面太远，就认为这是一个拟合的不好的平面
                for (int j = 0; j < 5; j++) {
                  if (fabs(pa * laserCloudSurfFromMap->points[pointSearchInd[j]].x +
                      pb * laserCloudSurfFromMap->points[pointSearchInd[j]].y +
                      pc * laserCloudSurfFromMap->points[pointSearchInd[j]].z + pd) > 0.2) {
                    planeValid = false;
                    break;
                  }
                }

                if (planeValid) {
                  float pd2 = pa * pointSel.x + pb * pointSel.y + pc * pointSel.z + pd;

                  //unused
                  pointProj = pointSel;
                  pointProj.x -= pa * pd2;
                  pointProj.y -= pb * pd2;
                  pointProj.z -= pc * pd2;

                  float s = 1 - 0.9 * fabs(pd2) / sqrt(sqrt(pointSel.x * pointSel.x
                          + pointSel.y * pointSel.y + pointSel.z * pointSel.z));

                  coeff.x = s * pa;
                  coeff.y = s * pb;
                  coeff.z = s * pc;
                  coeff.intensity = s * pd2;

                  if (s > 0.1) {
                    laserCloudOri->push_back(pointOri);
                    coeffSel->push_back(coeff);
                  }
                }
              }
            }

七、高斯牛顿优化与退化处理

这一部分与laserOdometry完全一样，直接复制过来啦！

7.1 雅克比矩阵求解与高斯牛顿优化

在代码中，作者是纯手推的高斯牛顿算法，这种方式相比于使用Ceres等工具，会提高运算速度，但是计算雅克比矩阵比较麻烦，需要清晰的思路和扎实的数学功底，下面我们一起来推导一下。

以edge point匹配为例，planar point是一样的。

设误差函数(点到直线的距离)为：
$$f(X)=D(p_{start}^i,p_{start}^t)$$
其中，X为待优化变量，也就是transform[6]中存储的变量，表示3轴旋转rx、ry、rz和3轴平移量tx、ty、tz；D()表示两点之间的距离，其计算公式为：
$$D(p_{start}^i,p_{start}^t)=\sqrt{(p_{start}^i-p_{start}^t{)}^T(p_{start}^i-p_{start}^t)}$$

$p_{start}^i$表示start时刻坐标系下待匹配点i；$p_{start}^t$表示start时刻坐标系下点i到直线jl的垂点；另外根据之前TransformToStart()函数推导过的坐标变换有：
p s t a r t i = R c u r r _ s t a r t − 1 ∗ ( p c u r r − 1 − t c u r r _ s t a r t ) = [ c r y c r z − s r x s r y s r z − c r y s r z + s r x s r y c r z − c r x s r y − c r x s r z c r x c r z s r x s r y c r z + s r x c r y s r z s r y s r z − s r x c r y c r z c r x c r y ] ⋅ [ p c u r r − t x p c u r r − t y p c u r r − t z ] p_{start}^i = R_{curr\_start}^{-1}*(p_{curr}^{-1}-t_{curr\_start}) = \left[ \begin{matrix} crycrz-srxsrysrz& -crysrz+srxsrycrz& -crxsry\\ -crxsrz& crxcrz& srx\\ srycrz+srxcrysrz& srysrz-srxcrycrz& crxcry\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} p_{curr}-tx\\ p_{curr}-ty\\ p_{curr}-tz\\ \end{array} \right] pstarti​=Rcurr_start−1​∗(pcurr−1​−tcurr_start​)= ​crycrz−srxsrysrz−crxsrzsrycrz+srxcrysrz​−crysrz+srxsrycrzcrxcrzsrysrz−srxcrycrz​−crxsrysrxcrxcry​ ​⋅ ​pcurr​−txpcurr​−typcurr​−tz​ ​

根据链式法则，f(x)对X求导有：
$$\frac{\partial f(x)}{\partial X}=\frac{\partial f(x)}{\partial D(p_{start}^i,p_{start}^t)}\ast \frac{\partial D(p_{start}^i,p_{start}^t)}{\partial p_{start}^i}\ast \frac{\partial p_{start}^i}{\partial X}$$

对其中每一项进行计算：
$$\begin{gathered} \frac{\partial f(x)}{\partial D(p_{start}^i,p_{start}^t)}=1 \\ \frac{\partial D(p_{start}^i,p_{start}^t)}{\partial p_{start}^i}=\frac{\partial \sqrt{(p_{start}^i-p_{start}^t{)}^T(p_{start}^i-p_{start}^t)}}{\partial p_{start}^i}=\frac{p_{start}^i-p_{start}^t}{D(p_{start}^i,p_{start}^t)} \end{gathered}$$
D对$p_{start}^i$求导的结果其实就是 进行归一化后的点到直线向量，它在xyz三个轴的分量就是前面求解出来的la、lb、lc变量。

$$\frac{\partial p_{start}^i}{\partial X}=\frac{\partial R_{curr\_start}^{-1}\ast (p_{curr}^{-1}-t_{curr\_start})}{\partial [rx,ry,rz,tx,ty,tz{]}^T}$$

用上面$p_{start}^i$的结果，分别对rx,ry,rz,tx,ty,tz求导，将得到的结果(3x6矩阵)再与D对$p_{start}^i$求导的结果(1x3矩阵)相乘，就可以得到代码中显示的结果(1x6矩阵)，分别赋值到matA的6个位置，matB是残差项。

最后使用opencv的QR分解求解增量X即可。

            float srx = sin(transformTobeMapped[0]);
            float crx = cos(transformTobeMapped[0]);
            float sry = sin(transformTobeMapped[1]);
            float cry = cos(transformTobeMapped[1]);
            float srz = sin(transformTobeMapped[2]);
            float crz = cos(transformTobeMapped[2]);

            int laserCloudSelNum = laserCloudOri->points.size();
            if (laserCloudSelNum < 50) {//如果特征点太少
              continue;
            }

            cv::Mat matA(laserCloudSelNum, 6, CV_32F, cv::Scalar::all(0));
            cv::Mat matAt(6, laserCloudSelNum, CV_32F, cv::Scalar::all(0));
            cv::Mat matAtA(6, 6, CV_32F, cv::Scalar::all(0));
            cv::Mat matB(laserCloudSelNum, 1, CV_32F, cv::Scalar::all(0));
            cv::Mat matAtB(6, 1, CV_32F, cv::Scalar::all(0));
            cv::Mat matX(6, 1, CV_32F, cv::Scalar::all(0));
            //构建雅可比矩阵和残差
            for (int i = 0; i < laserCloudSelNum; i++) {
              pointOri = laserCloudOri->points[i];
              coeff = coeffSel->points[i];

              float arx = (crx*sry*srz*pointOri.x + crx*crz*sry*pointOri.y - srx*sry*pointOri.z) * coeff.x
                        + (-srx*srz*pointOri.x - crz*srx*pointOri.y - crx*pointOri.z) * coeff.y
                        + (crx*cry*srz*pointOri.x + crx*cry*crz*pointOri.y - cry*srx*pointOri.z) * coeff.z;

              float ary = ((cry*srx*srz - crz*sry)*pointOri.x 
                        + (sry*srz + cry*crz*srx)*pointOri.y + crx*cry*pointOri.z) * coeff.x
                        + ((-cry*crz - srx*sry*srz)*pointOri.x 
                        + (cry*srz - crz*srx*sry)*pointOri.y - crx*sry*pointOri.z) * coeff.z;

              float arz = ((crz*srx*sry - cry*srz)*pointOri.x + (-cry*crz-srx*sry*srz)*pointOri.y)*coeff.x
                        + (crx*crz*pointOri.x - crx*srz*pointOri.y) * coeff.y
                        + ((sry*srz + cry*crz*srx)*pointOri.x + (crz*sry-cry*srx*srz)*pointOri.y)*coeff.z;

              matA.at<float>(i, 0) = arx;
              matA.at<float>(i, 1) = ary;
              matA.at<float>(i, 2) = arz;
              matA.at<float>(i, 3) = coeff.x;
              matA.at<float>(i, 4) = coeff.y;
              matA.at<float>(i, 5) = coeff.z;
              matB.at<float>(i, 0) = -coeff.intensity;
            }
            cv::transpose(matA, matAt);
            matAtA = matAt * matA;      // H = J^T * J
            matAtB = matAt * matB;      // g = -J^T * e
            cv::solve(matAtA, matAtB, matX, cv::DECOMP_QR);

7.2 退化处理

代码中使用的退化处理在Ji Zhang的这篇论文(《On Degeneracy of Optimization-based State Estimation Problems》)中有详细论述。

简单来说，作者认为退化只可能发生在第一次迭代时，先对$H=J^T\ast J$矩阵求特征值，然后将得到的特征值与阈值(代码中为10)进行比较，如果小于阈值则认为该特征值对应的特征向量方向发生了退化，将对应的特征向量置为0，然后按照论文中所述，计算一个P矩阵：
$$P=V_f^{-1}\ast V_u$$

$V_f$是原来的特征向量矩阵，$V_u$是将退化方向置为0后的特征向量矩阵，然后用P矩阵与原来得到的解相乘，得到最终解：

$$X‘=P\ast X^{\ast }$$

            //退化场景判断与处理
            if (iterCount == 0) {
              cv::Mat matE(1, 6, CV_32F, cv::Scalar::all(0));
              cv::Mat matV(6, 6, CV_32F, cv::Scalar::all(0));
              cv::Mat matV2(6, 6, CV_32F, cv::Scalar::all(0));

              cv::eigen(matAtA, matE, matV);
              matV.copyTo(matV2);

              isDegenerate = false;
              float eignThre[6] = {100, 100, 100, 100, 100, 100};
              for (int i = 5; i >= 0; i--) {
                if (matE.at<float>(0, i) < eignThre[i]) {
                  for (int j = 0; j < 6; j++) {
                    matV2.at<float>(i, j) = 0;
                  }
                  isDegenerate = true;
                } else {
                  break;
                }
              }
              matP = matV.inv() * matV2;
            }

            if (isDegenerate) {
              cv::Mat matX2(6, 1, CV_32F, cv::Scalar::all(0));
              matX.copyTo(matX2);
              matX = matP * matX2;
            }

            //积累每次的调整量
            transformTobeMapped[0] += matX.at<float>(0, 0);
            transformTobeMapped[1] += matX.at<float>(1, 0);
            transformTobeMapped[2] += matX.at<float>(2, 0);
            transformTobeMapped[3] += matX.at<float>(3, 0);
            transformTobeMapped[4] += matX.at<float>(4, 0);
            transformTobeMapped[5] += matX.at<float>(5, 0);

            float deltaR = sqrt(
                                pow(rad2deg(matX.at<float>(0, 0)), 2) +
                                pow(rad2deg(matX.at<float>(1, 0)), 2) +
                                pow(rad2deg(matX.at<float>(2, 0)), 2));
            float deltaT = sqrt(
                                pow(matX.at<float>(3, 0) * 100, 2) +
                                pow(matX.at<float>(4, 0) * 100, 2) +
                                pow(matX.at<float>(5, 0) * 100, 2));

            //旋转平移量足够小就停止迭代
            if (deltaR < 0.05 && deltaT < 0.05) {
              break;
            }
          }

7.3 更新变换矩阵–transformUpdate()函数

迭代优化完成后，使用transformUpdate()函数进行变换矩阵的优化，主要是完成对transformBefMapped[6]和transformAftMapped[6]的更新。

如果有IMU的话，就使用IMU信息中的roll和pitch角对结果中的变量进行微调，微调的原理我也没太看懂，感觉就是稍微加了一点点补偿。

然后将transformBefMapped[6]更新为当前帧相对于初始帧的变换$T_{init\_end}$；将transformAftMapped[6]更新更新为优化后的当前帧相当于地图坐标系的变换$T_{map\_end}$

//优化后进行变换矩阵的更新，如果有IMU的，则使用IMU进行补偿
void transformUpdate()
{
  if (imuPointerLast >= 0) {
    float imuRollLast = 0, imuPitchLast = 0;
    //查找点云时间戳小于imu时间戳的imu位置
    while (imuPointerFront != imuPointerLast) {
      if (timeLaserOdometry + scanPeriod < imuTime[imuPointerFront]) {
        break;
      }
      imuPointerFront = (imuPointerFront + 1) % imuQueLength;
    }

    if (timeLaserOdometry + scanPeriod > imuTime[imuPointerFront]) {//未找到,此时imuPointerFront==imuPointerLast
      imuRollLast = imuRoll[imuPointerFront];
      imuPitchLast = imuPitch[imuPointerFront];
    } else {
      int imuPointerBack = (imuPointerFront + imuQueLength - 1) % imuQueLength;
      float ratioFront = (timeLaserOdometry + scanPeriod - imuTime[imuPointerBack]) 
                       / (imuTime[imuPointerFront] - imuTime[imuPointerBack]);
      float ratioBack = (imuTime[imuPointerFront] - timeLaserOdometry - scanPeriod) 
                      / (imuTime[imuPointerFront] - imuTime[imuPointerBack]);

      //按时间比例求翻滚角和俯仰角
      imuRollLast = imuRoll[imuPointerFront] * ratioFront + imuRoll[imuPointerBack] * ratioBack;
      imuPitchLast = imuPitch[imuPointerFront] * ratioFront + imuPitch[imuPointerBack] * ratioBack;
    }

    //imu稍微补偿俯仰角和翻滚角
    transformTobeMapped[0] = 0.998 * transformTobeMapped[0] + 0.002 * imuPitchLast;
    transformTobeMapped[2] = 0.998 * transformTobeMapped[2] + 0.002 * imuRollLast;
  }

  //记录优化之前与之后的转移矩阵
  for (int i = 0; i < 6; i++) {
    transformBefMapped[i] = transformSum[i];
    transformAftMapped[i] = transformTobeMapped[i];
  }
}

八、将当前帧的特征点加入到地图中

下面两个for循环作用是：将当前帧的特征点按照cube索引号放入地图中，用于之后的匹配；然后对周围点云S`进行一次降采样，更新地图。

        /*下面两个for循环作用是：将当前帧的特征点放入地图中，用于之后的匹配*/
        //将corner points按距离（比例尺缩小）归入相应的立方体
        for (int i = 0; i < laserCloudCornerStackNum; i++) {
          //转移到世界坐标系
          pointAssociateToMap(&laserCloudCornerStack->points[i], &pointSel);

          //按50的比例尺缩小，四舍五入，偏移laserCloudCen*的量，计算索引
          int cubeI = int((pointSel.x + 25.0) / 50.0) + laserCloudCenWidth;
          int cubeJ = int((pointSel.y + 25.0) / 50.0) + laserCloudCenHeight;
          int cubeK = int((pointSel.z + 25.0) / 50.0) + laserCloudCenDepth;

          if (pointSel.x + 25.0 < 0) cubeI--;
          if (pointSel.y + 25.0 < 0) cubeJ--;
          if (pointSel.z + 25.0 < 0) cubeK--;

          if (cubeI >= 0 && cubeI < laserCloudWidth && 
              cubeJ >= 0 && cubeJ < laserCloudHeight && 
              cubeK >= 0 && cubeK < laserCloudDepth) {//只挑选-laserCloudCenWidth * 50.0 < point.x < laserCloudCenWidth * 50.0范围内的点，y和z同理
              //按照尺度放进不同的组，每个组的点数量各异
            int cubeInd = cubeI + laserCloudWidth * cubeJ + laserCloudWidth * laserCloudHeight * cubeK;
            laserCloudCornerArray[cubeInd]->push_back(pointSel);
          }
        }

        //将surf points按距离（比例尺缩小）归入相应的立方体
        for (int i = 0; i < laserCloudSurfStackNum; i++) {
          pointAssociateToMap(&laserCloudSurfStack->points[i], &pointSel);

          int cubeI = int((pointSel.x + 25.0) / 50.0) + laserCloudCenWidth;
          int cubeJ = int((pointSel.y + 25.0) / 50.0) + laserCloudCenHeight;
          int cubeK = int((pointSel.z + 25.0) / 50.0) + laserCloudCenDepth;

          if (pointSel.x + 25.0 < 0) cubeI--;
          if (pointSel.y + 25.0 < 0) cubeJ--;
          if (pointSel.z + 25.0 < 0) cubeK--;

          if (cubeI >= 0 && cubeI < laserCloudWidth && 
              cubeJ >= 0 && cubeJ < laserCloudHeight && 
              cubeK >= 0 && cubeK < laserCloudDepth) {
            int cubeInd = cubeI + laserCloudWidth * cubeJ + laserCloudWidth * laserCloudHeight * cubeK;
            laserCloudSurfArray[cubeInd]->push_back(pointSel);
          }
        }

        //因为加入了当前sweep的点，所以这个for循环对局部点云集合S`进行降采样，然后更新总cube集合
        for (int i = 0; i < laserCloudValidNum; i++) {
          int ind = laserCloudValidInd[i];  //局部点云集合S`的cube序号

          laserCloudCornerArray2[ind]->clear();
          downSizeFilterCorner.setInputCloud(laserCloudCornerArray[ind]);
          downSizeFilterCorner.filter(*laserCloudCornerArray2[ind]);//滤波输出到Array2

          laserCloudSurfArray2[ind]->clear();
          downSizeFilterSurf.setInputCloud(laserCloudSurfArray[ind]);
          downSizeFilterSurf.filter(*laserCloudSurfArray2[ind]);

          //Array与Array2交换，即滤波后自我更新
          pcl::PointCloud<PointType>::Ptr laserCloudTemp = laserCloudCornerArray[ind];
          laserCloudCornerArray[ind] = laserCloudCornerArray2[ind];
          laserCloudCornerArray2[ind] = laserCloudTemp;
          //laserCloudCornerArray更新成降采样之后的了

          laserCloudTemp = laserCloudSurfArray[ind];
          laserCloudSurfArray[ind] = laserCloudSurfArray2[ind];
          laserCloudSurfArray2[ind] = laserCloudTemp;
        }

九、话题发布

最后就是一些发提的发布，包括以下话题：

• /laser_cloud_surround：每隔5帧发布一次(这种一般都是用于可视化的情况)，降采样后的周围点云(不只是视域范围内的，而且周围的全部发布)
• /velodyne_cloud_registered：变换到地图坐标系下的全部点云
• /aft_mapped_to_init：经过laserMapping优化后的当前帧到初始时刻(或者到地图map坐标系)的坐标变换

并且广播了/camera_init到/aft_mapped的坐标变换

        mapFrameCount++;
        //特征点汇总降采样，每隔五帧publish一次，从第一次开始
        if (mapFrameCount >= mapFrameNum) {// 每隔5帧发布S`集合
          mapFrameCount = 0;

          laserCloudSurround2->clear();
          for (int i = 0; i < laserCloudSurroundNum; i++) {
            int ind = laserCloudSurroundInd[i]; // 局部地图所有cube序号
            *laserCloudSurround2 += *laserCloudCornerArray[ind];
            *laserCloudSurround2 += *laserCloudSurfArray[ind];
          }

          laserCloudSurround->clear();
          downSizeFilterCorner.setInputCloud(laserCloudSurround2);
          downSizeFilterCorner.filter(*laserCloudSurround);

          sensor_msgs::PointCloud2 laserCloudSurround3;
          pcl::toROSMsg(*laserCloudSurround, laserCloudSurround3);
          laserCloudSurround3.header.stamp = ros::Time().fromSec(timeLaserOdometry);
          laserCloudSurround3.header.frame_id = "/camera_init";
          pubLaserCloudSurround.publish(laserCloudSurround3);
        }

        //将点云中全部点转移到世界坐标系下
        int laserCloudFullResNum = laserCloudFullRes->points.size();
        for (int i = 0; i < laserCloudFullResNum; i++) {
          pointAssociateToMap(&laserCloudFullRes->points[i], &laserCloudFullRes->points[i]);
        }

        sensor_msgs::PointCloud2 laserCloudFullRes3;
        pcl::toROSMsg(*laserCloudFullRes, laserCloudFullRes3);
        laserCloudFullRes3.header.stamp = ros::Time().fromSec(timeLaserOdometry);
        laserCloudFullRes3.header.frame_id = "/camera_init";
        pubLaserCloudFullRes.publish(laserCloudFullRes3);

        geometry_msgs::Quaternion geoQuat = tf::createQuaternionMsgFromRollPitchYaw
                                  (transformAftMapped[2], -transformAftMapped[0], -transformAftMapped[1]);

        odomAftMapped.header.stamp = ros::Time().fromSec(timeLaserOdometry);
        odomAftMapped.pose.pose.orientation.x = -geoQuat.y;
        odomAftMapped.pose.pose.orientation.y = -geoQuat.z;
        odomAftMapped.pose.pose.orientation.z = geoQuat.x;
        odomAftMapped.pose.pose.orientation.w = geoQuat.w;
        odomAftMapped.pose.pose.position.x = transformAftMapped[3];
        odomAftMapped.pose.pose.position.y = transformAftMapped[4];
        odomAftMapped.pose.pose.position.z = transformAftMapped[5];
        //扭转量
        odomAftMapped.twist.twist.angular.x = transformBefMapped[0];
        odomAftMapped.twist.twist.angular.y = transformBefMapped[1];
        odomAftMapped.twist.twist.angular.z = transformBefMapped[2];
        odomAftMapped.twist.twist.linear.x = transformBefMapped[3];
        odomAftMapped.twist.twist.linear.y = transformBefMapped[4];
        odomAftMapped.twist.twist.linear.z = transformBefMapped[5];
        pubOdomAftMapped.publish(odomAftMapped);

        //广播坐标系旋转平移参量
        aftMappedTrans.stamp_ = ros::Time().fromSec(timeLaserOdometry);
        aftMappedTrans.setRotation(tf::Quaternion(-geoQuat.y, -geoQuat.z, geoQuat.x, geoQuat.w));
        aftMappedTrans.setOrigin(tf::Vector3(transformAftMapped[3], 
                                             transformAftMapped[4], transformAftMapped[5]));
        tfBroadcaster.sendTransform(aftMappedTrans);

      }
    }

    status = ros::ok();
    rate.sleep();
  }

  return 0;
}

总结

我个人感觉laserMapping这个模块是比laserOdometry模块简单很多的，主要是不涉及到IMU就省很多事，我觉得这部分需要仔细想一想的地方就是地图维护更新的那一部分，中间优化部分很简单，laserOdometry中的那部分弄懂了这部分就很容易看明白了。

论文中说的这部分是低频率高精度，按照这个代码，它的频率是5Hz，但是只要改变一下控制跳帧变量，就很容易得到文章中的1Hz；高精度我觉得主要是体现在它使用的是scan-to-map的方式进行匹配，用于匹配的数据量很大，从而提高了匹配精度，因为它的迭代次数是比laserOdometry少的。

下一篇将介绍最后一个模块transformMaintenance.cpp，也就是laserOdometry和laserMapiing求解到的变量进行融合得到最终变换的模块。