算法通过村第四关-栈黄金笔记|表达式问题

---

前言

---

提示：快乐的人没有过去，不快乐的人除了过去一无所有。 --理查德·弗兰纳根《深入北方的小路》

栈的进阶来了，还记得栈的使用场景吗？表达式和符号，这不就来了

1. 计算器问题

参考题目介绍：227. 基本计算器 II - 力扣（LeetCode）


计算问题在栈的运用也是非常广泛的。在乘除优先于加减计算，我们需要考虑所有的乘除运算，并将这些乘除运算后的整数放回原来对应的表达式中，随后整个表达式的值等于一系列整数加减后的运算值。

基于这样的想法，我们可以使用的们的老朋友栈了，保存这些（进行乘除运算后的）整数值。对于加减后的数字，将其直接压入栈中，对于乘除后的数字，我可以直接与栈顶元素计算，并替换栈顶元素作为计算后的结果。

具体来说，我们遍历字符串s，并用变量preSign来记录每个数字之前的运算符，对于第一个数字，其之前的运算符视为加号。每次遍历到数组的末尾时，根据preSign来决定计算方式

• 加号：将数字压入栈中
• 减号：将数字的相反数压入栈中
• 乘除号：计算数字与栈顶元素，并将栈顶元素替换为计算结果。

代码实现中，读到一个运算符，或者遍历到字符串末尾,，就认为遍历到了数字末尾。处理完该数字后，更新preSign为当前遍历的字符。遍历完字符串s后，将栈中的元素累加，即为该表达式的结果。

	 /**
     * 实现计算器问题
     * @param s
     * @return
     */
    public static int calculate(String s) {
        Deque<Integer> stack = new ArrayDeque<Integer>();
        // 计算可以都看做时 +   这里是前一个符号
        Character preSign = '+';
        int num = 0;
        int n = s.length();
        for (int i = 0; i < n; i++) {
            if (Character.isDigit(s.charAt(i))) {
                // 字符转数字  考虑到大于10 的情况
                num = num * 10 + s.charAt(i) - '0';
            }
            if (!Character.isDigit(s.charAt(i)) && s.charAt(i) != ' ' || i == n - 1) {
                switch (preSign) {
                    case '+':
                        stack.push(num);
                        break;
                    case '-':
                        stack.push(-num);
                        break;
                    case '*': // 5 * 2
                        stack.push(stack.pop() * num);
                        break;
                    case '/':  // 10 / 2
                        stack.push(stack.pop() / num);
                        break;
                    default:
                        break;
                }
                // 更新前一个符号   这样就可以确定乘除优先了
                preSign = s.charAt(i);
                num = 0;
            }
        }
        int ans = 0;
        while(!stack.isEmpty()){
            ans += stack.pop();
        }
        return ans;
    }

注意：

• perSign 指的是前一个运算符号（首次默认看作是＋号）

• 慢一次计算 就可以确保乘除优先了

2. 逆波兰表达式问题

参考题目介绍：150. 逆波兰表达式求值 - 力扣（LeetCode）


说实话这个题颇有难度，可以放在学习完二叉树再来看⭐⭐

表达式计算式编译原理，自然语言处理，文本分析等领域非常看重的问题，这里我们就挑这个题目练手，逆波兰表达式。

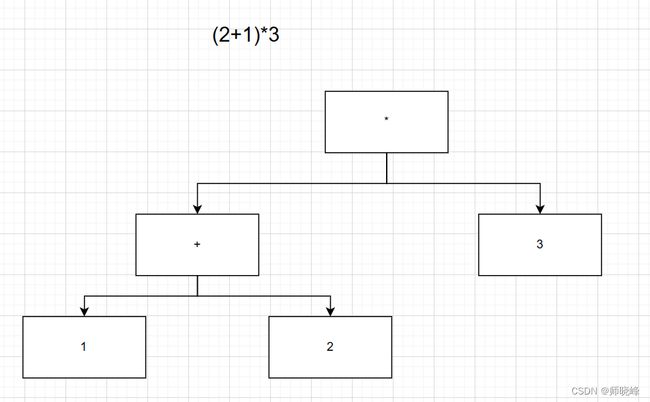
这道题看似困难，实则真困难呐，你要是不知道什么是表达式，完了，你不会了。这里的表达式就好比一起上小学学的（2+1）* 3这样字的，根据不同的记法，就有前缀，中缀，后缀之说，区别呢在于运算符号相对于操作数的位置，前缀就是运算符号在操作数前面，那后缀和中缀呢？你想想？

聪明讲个笑话：

有一天，一只蚂蚁遇到了一只蜗牛。蚂蚁问蜗牛：“为什么我们走路的时候总是把头抬得那么高？”蜗牛回答：“因为我们的目标在地上。”

对应的三种表达式：

中缀表达式：（ 1 + 2 ） * 3
前缀表达式： + 1 2 * 3
后缀表达式： 1 2 + 3 *

从上面看，中缀的表达式更像是我们常见的，它作为一种通用的算数运算和逻辑公式表示，操作符以中缀形式处于操作数的中间。虽然我们的大脑很容易就可以理解这些分析最终拿到结果，但是对于计算机来说，就很头疼了，计算机在做表达式计算的时候，通常是需要将中缀表达式转换为前缀或者后缀表达式再进行求值的。前缀表达式的运算符位于两个相应操作数之前，前缀表达式又被称为前缀记法或者波兰是，而后缀表达式就是你波兰式了。

观察后我们就可以看出，根据特点将数字保存下来，遇到符号就计算。比如：1 2 + 3 * 遇到+ ，我们就好1 和 2 加起来，得到结果 3 然后在进行计算 得到结果 9 .

这样得话之不是容易一些，遇到数字就进栈，遇到运算符就取出栈中的最上面的两个元素进行计算，最后再将结果入栈。实现代码会不会简单一些：

public class EvalRPN {
    public static int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<Integer>();
        for (String token : tokens) {
            if (!Character.isDigit(token.charAt(0)) && token.length() == 1) {
                // 取出栈顶的数字
                int a = stack.pop();
                int b = stack.pop();
                // 做运算
                switch (token) {
                    case "+":   // a b +
                        stack.push(a + b);
                        break;
                    case "-": // a b -
                        stack.push(a - b);
                        break;
                    case "*": // a b *
                        stack.push(a * b);
                        break;
                    case "/": // a b /
                        stack.push(a / b);
                        break;
                    default:
                        break;
                }
            }else {
                // 直接存入栈中
                stack.push(Integer.parseInt(token));
            }
        }
        return  stack.pop();
    }

---

总结

提示：栈的运用，表达式策略，逆波兰。