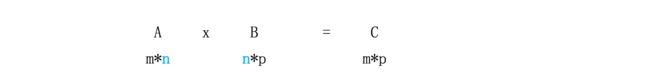03矩阵的乘法与逆矩阵

矩阵的乘法和逆矩阵

Multiplication & inverse matrices

​ 两个矩阵间的乘法、逆矩阵存在的条件、求解逆矩阵的方法

矩阵乘法

我们通过四种方法讨论如何使矩阵 A 与 B 相乘得到矩阵 C。其中 A 为 mn（m
行 n 列）矩阵，而 B 为 np 矩阵，则 C 为 mp 矩阵，记 cij为矩阵 C 中第 i 行第 j
列的元素。

• 矩阵乘法最常见求解方式

• 列组合与行组合方式

（1）列组合：

这种方法的关键就是将右侧矩阵 B 看做列向量组合，将问题转化为矩阵与向 量的乘法问题。也表明了矩阵 C 就是矩阵 A 中各列向量的线性组合，而 B 其实 是在告诉我们，要以什么样的方式组合 A 中的列向量。

（2）行组合

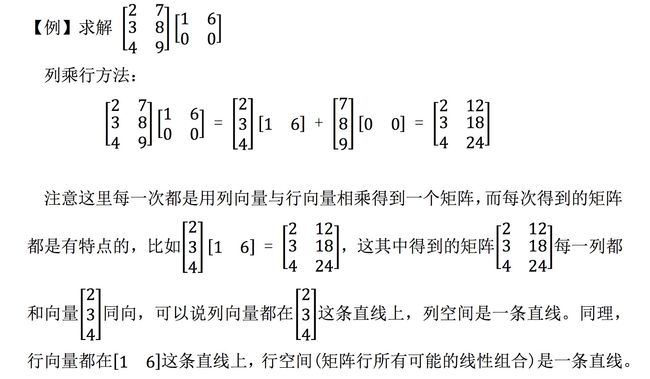
（3）列乘以行

（4）分块相乘

分块乘法就是宏观上的矩阵乘法，比如现在有一个 5050 的矩阵与 5050 矩 阵相乘，一个一个进行运算很麻烦，尤其是如果矩阵在某一区域上有一定的性质， 那么我们可以将其分块，如：

逆矩阵

（1）逆矩阵初识

（2）逆矩阵求解

（3）高斯-若尔当方法方法