金融风控数据分析-信用评分卡建模(附数据集下载地址)

本文引用自：

金融风控：信用评分卡建模流程 - 知乎 (zhihu.com)

在原文的基础上加上了一部分自己的理解，转载在CSDN上作为保留记录。

本文涉及到的数据集可直接从天池上面下载：

Give Me Some Credit给我一些荣誉_数据集-阿里云天池 (aliyun.com)

正文：

信用评分卡是一种常用的金融风控手段，其主要是通过建立一套计分规则，然后根据客户的各项属性来匹配计分规则，最终得到客户的风险评分。根据评分结果来选择是否进行授信或划分不同的授信额度和利率，以降低金融交易过程中的损失风险。信用评分卡有一套完整的开发流程，本文将试图从评分卡建立所涉及的背景知识，评分卡建立的基本流程两个方面来从整体上理解信用评分卡的作用以及建模方法。

1. 信用评分卡

顾名思义，评分卡是一张有分数刻度和相应阈值的表。对于一个客户，可以根据他的一系列信息找到对应的分数，最终进行汇总来量化这个客户将为本次的交易所带来的风险。由Fair Isaac公司开发的FICO系列评分卡是信用评分卡的始祖。如图1所示，FICO通过客户的年龄，住房以及收入情况来进行评分，每一项指标都有一定的阈值范围，落入不同的阈值范围就有相应的得分，最终的得分是所有指标得分的总分。这种评分手段操作简单，易于理解。评分卡按照不同的使用场景主要分为三类：

1）A卡（Application Card），即申请评分卡，主要是用于贷前审批。在此阶段，主要利用用户的外部征信数据、资产质量数据或过往平台表现（复贷）来衡量用户的信用情况。以初步筛选出信用良好的客户进行授信。

2）B卡（Behavior Card），即行为评分卡，主要是用于贷中阶段。即用户已经申请并获得了相应的贷款，用于动态评估客户在未来某一阶段的逾期风险，进而调整额度或利率等以减少损失

3）C卡（Collection Card），即催收评分卡，主要是用于贷后管理。即用户此时已经出现逾期情况，需要制定合理的催收策略以尽可能减少逾期带来的损失。此时根据C卡评分来优化贷后管理策略，实现催收资源的合理配置

图1 FICO评分卡

类似FICO这种静态的评分卡最大的优点在于操作简单，可解释性强。但随着时间的推移，目标客群会不断发生变化，这种静态的方式难以满足需求。于是，基于机器学习模型的信用评分卡展现出了更大的潜力。其能够根据数据的变化去动态调整不同特征的权重，从而不断迭代以适应新的数据模式。在风控领域，为了提高信用评分卡的可解释性，通常采用逻辑回归模型来进行评分卡的建模。在下一节中，将使用Kaggle上的Give me credit card数据来从0到1建立一个信用评分卡，从中梳理出评分卡的常规建模流程。在建模期间也会穿插介绍其中涉及的一些重要概念，理解这些概念背后的原理才能明白做这一步的含义是什么。

2. 信用评分卡建模流程

2.1 探索性数据分析（EDA）

EDA主要是利用各种统计分析的手段来从整体上了解数据的情况，包括数据的构成，数据的质量，数据的含义等。以便后续针对特定的问题制定合理的数据预处理方案，完成特征工程的工作

1. 特征释义

本次采用的数据集包括12个特征，其中有效特征为11个（一个Uname0特征）。各个特征的具体含义如下。

• SeriousDlqin2yrs：超过90天或更糟的逾期拖欠，是用户的标签，0，1分别表示未逾期和逾期
• RevolvingUtilizationOfUnsecuredLines：除了房贷车贷之外的信用卡账面金额（即贷款金额）/信用卡总额度
• age：贷款人年龄
• NumberOfTime30-59DaysPastDueNotWorse：借款人逾期30-59天的次数
• DebtRatio：负债比率，每月债务、赡养费、生活费/每月总收入
• MonthlyIncome：月收入
• NumberOfOpenCreditLinesAndLoans：开放式信贷和贷款数量，开放式贷款（分期付款如汽车贷款或抵押贷款）和信贷（如信用卡）的数量
• NumberOfTimes90DaysLate：借款者有90天或更高逾期的次数
• NumberRealEstateLoansOrLines：包括房屋净值信贷额度在内的抵押贷款和房地产贷款数量
• NumberOfTime60-89DaysPastDueNotWorse：借款人逾期60-89天的次数
• NumberOfDependents：不包括本人在内的家属数量

2. 数据基本情况

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt 
df_train = pd.read_csv("./data/cs-training.csv")
df_test = pd.read_csv("./data/cs-test.csv")
df_all = pd.concat([df_train,df_test])
print("train size:",len(df_train))
print("test size:",len(df_test))
print(df_all.info())

数据集总共包含251503条数据，其中训练集有150000条数据，测试集有101503条数据。MonthlyIncome 和 NumberOfDependents有缺失值，由于缺失并不严重，因此予以保留，后续进行插补。

3. 异常值检测

这里采用3西格玛原则从各个特征中检测异常值并进行统计，以了解数据中异常值的情况

#异常检测
def review_outlier(x,lower,upper):
    '''
    根据3-西格玛方法检测出特征中的异常值
    '''
    if x < lower or x > upper:
        return True
    return False
df_outlier_train = df_train.copy()
k = 3.0

for fea in df_outlier_train.columns:
    lower = df_outlier_train[fea].mean() -  k*df_outlier_train[fea].std()
    upper = df_outlier_train[fea].mean() +  k*df_outlier_train[fea].std()
   
    outlier = df_outlier_train[fea]\
    .apply(review_outlier,args=(lower,upper))
    print("{} 异常值数量：{}".format(fea,outlier.sum()))

NumberOfOpenCreditLinesAndLoans以及NumberRealEstateLoansOrLines的异常值数量较大。从数据的角度而言这两个特征可以考虑剔除或删除有异常的数据，但从业务角度而言，这两个特征与逾期风险可能存在较大的关联，所以最终还是保留这两个特征。

4. 描述性统计

sns.countplot(x='SeriousDlqin2yrs',data=df_train)

从标签的分布来看，样本中的好客户占比明显高于坏客户，意味着后续需要进行数据的平衡，避免模型过度倾向于将样本预测为好客户。

#对数据中的好坏客户的年龄分布进行统计
bad = df_train[df_train['SeriousDlqin2yrs']==1].index
good = df_train[df_train['SeriousDlqin2yrs']==0].index
fig,ax = plt.subplots(2,1,figsize=[6,6])
fig.subplots_adjust(hspace=0.5)
sns.distplot(df_train.loc[bad,'age'],ax=ax[0])
ax[0].set_title("bad customer")
sns.distplot(df_train.loc[good,'age'],ax=ax[1])
ax[1].set_title("good customer")
print("坏客户年龄统计\n",df_train.loc[bad,'age'].describe())
print("好客户年龄统计\n",df_train.loc[good,'age'].describe())

从频率分布图的形状来看，好坏客户的年龄分布整体上都符合正态分布，符合统计学的概念。其中，坏客户和好客户的年龄均值分别为45.9和52.8，坏客户的年龄略低于好客户的年龄。好客户中年龄最小值为0岁，年龄最大值为109岁，这不太符合常规的借贷业务客群特征，考虑可能是异常值，后续需要进行处理。

5. 变量显著性检验

ps: 这里涉及到变量之间检验方法

该问题预测变量X是每个特征的值，反应变量Y是"bad"，”good”类别，这里做两样本T检验的目的是为了观察类别为bad的特征和类别为good的特征是否为有显著差异，而两样本T检验是为了判别两类别均值是否相等。对于分类问题来说，我们可以粗略的认为分类后的样本均值距离越远分的越好（类间距离）所以，T检验在该问题中可以用来判断某一特征对于分类“bad”,"good"是否有显著差异（有显著差异的话说明该特征对于分类是有正向作用的）

下面这个帖子详细讲述了T检验的用法。

双样本T检验——机器学习特征工程相关性分析实战 - 知乎

这里主要是想观察同一个特征在不同标签的客户群体中的差异，若有显著差异，则表明该特征与客户是否逾期有显著的相关性，后续建模需要保留这部分特征，反之，可以进行特征过滤，初步筛选掉一些不重要的特征，降低模型的复杂度。这里采用scipy库中的ttest_ind来检验特征的在不同客群中的差异，通过Levene来确定方差齐性。定义p小于0.001时分布具有显著差异。

#变量显著性检验
from scipy.stats import levene,ttest_ind
bad = df_train[df_train['SeriousDlqin2yrs']==1].index
good = df_train[df_train['SeriousDlqin2yrs']==0].index
fea_pvalue = {}
for fea in df_train.columns[2:]:
    
    p_values = {}
    _, pvalue_l = levene(train_x.loc[bad,fea], train_x.loc[good,fea])

    # 当p>0.05时不能拒绝原假设，即认为方差对齐
    if pvalue_l > 0.05:
        _, p_values = ttest_ind(train_x.loc[bad,fea], train_x.loc[good,fea], equal_var=True)
        fea_pvalue[fea] = p_values
        
    else:
        _, p_values = ttest_ind(train_x.loc[bad,fea], train_x.loc[good,fea], equal_var=False)
        fea_pvalue[fea] = p_values
 
fea_pvalue = pd.DataFrame(fea_pvalue,index=[0]).T.rename(columns={0:'p-value'})
fea_pvalue

最终所有特征的p值均小于0.001，表示都具有显著差异，因此后续所有特征都可以考虑进入模型。

2.2 数据清洗与预处理

经过前一步的探索性数据分析后，我们发现数据中存在着缺失值和异常值，在数据预处理阶段需要进行处理。鉴于变量显著性检验中的结果，即所有特征都与逾期风险有显著的相关性，因此对于与缺失和异常值的处理均不采用删除特征的方式来进行。对于异常值，先将其替换为缺失值，最后再与缺失值进行统一的插补。对于数据不平衡问题，可以通过对少数样本进行增采样或对多数样本进行减采样的方式来保障类别的平衡。当然，这里也能够在模型训练阶段为不同类别的样本制定不同的权重，从而使得模型不会过度偏向占比较大的类别。这是根据前面探索性分析后制定的初步数据预处理方案，主要是针对数据质量的问题。在风控建模中还需要涉及到数据分箱，WOE编码，变量筛选等过程，主要是提升特征的表达能力，解决的是模型性能的问题，这些相关的数据处理细节将在后面逐步展开

1. 数据清洗

删除数据中的无效列名

df_train = df_train.drop(columns=['Unnamed: 0'])
df_test = df_test.drop(columns=['Unnamed: 0'])
from sklearn.model_selection import train_test_split

一般在进行建模之前，都需要将数据拆分成三份，即训练集，测试集和验证集。训练集是用于模型的训练拟合。验证集是在模型训练阶段与训练集配合使用来选择一些超参数或制定优化模型的策略。测试集主要是为了检验模型的拟合程度，泛化能力等。一般来讲，需要将数据按照时间来进行划分子集。比如有2020-01-01到2022-01-01的数据，那么可以选择最后一年的数据来作为验证集和测试集，其中两个子集各占半年。而第一年的数据作为训练集来训练模型。这样能够检验模型的跨时间稳定性。由于我们案例中使用的数据没有时间的标识，且测试集没有标签，所以这里将训练集随机拆分（7:3）成训练集和验证集，以模拟这一场景。

from sklearn.model_selection import train_test_split
#拆分数据，将训练集拆分成训练数据和验证数据，以检测特征和模型的稳定性等指标
train,valid = train_test_split(df_train,test_size=0.3,random_state=0)
train.reset_index(drop=True,inplace=True)
valid.reset_index(drop=True,inplace=True)
print("train size:{}".format(len(train)))
print("valid size:{}".format(len(valid)))
print("test size:{}".format(len(df_test)))

2. 异常值过滤和缺失插补

对于异常值的处理方法主要有三种，一是直接删除，二是替换为缺失值后进行插补，三是通过分箱将异常值单独作为一个分组看待。在这里以第二种方法进行处理，即把异常值视为缺失值。

k = 3.0
#使用3西格玛原则检测异常值，各个特征的均值和标准差以训练集计算，验证集和测试集直接使用
for fea in train.columns:
    if fea=='SeriousDlqin2yrs':
        continue
    lower = train[fea].mean() - k*train[fea].std()
    upper = train[fea].mean() +  k*train[fea].std()
    
    if_outlier_train = train[fea].apply(review_outlier,args=(lower,upper))
    if_outlier_val = valid[fea].apply(review_outlier,args=(lower,upper))
    if_outlier_test = df_test[fea].apply(review_outlier,args=(lower,upper))
    
    out_index_train = np.where(if_outlier_train)[0]
    out_index_val = np.where(if_outlier_val)[0]
    out_index_test = np.where(if_outlier_test)[0]
    #替换为空值
    train.loc[out_index_train,fea] = np.nan 
    valid.loc[out_index_val,fea] = np.nan
    df_test.loc[out_index_test,fea] = np.nan 

数据插补一般选用均值或中位数（连续变量），此外，根据3西格玛原则，可以通过生成均值加减三倍标准差范围内的随机数进行插补，但由于这份数据集中特征的标准差很大，数据分布比较分散，所以生成的随机数可能会是一个异常值（比如年龄为负数），因此这里以中位数来插补。注意，中位数是由训练集计算出来的，验证集和测试集直接使用。

#以特征的中位数插补数据
median = train.median()
train.fillna(median,inplace=True)
valid.fillna(median,inplace=True)
df_test.fillna(median,inplace=True) 
print(train.info())

3. 特征分箱

在风控建模过程中常常需要对变量进行分箱处理，主要是将连变量进行离散化处理形成类别变量，类别变量可以进行适当的合并。分箱的核心目标就是为了提升模型整体的稳定性。比如将异常值和缺失值单独作为一个分箱，使得模型对这些值不太敏感。另一方面，对于LR这种线性模型，分箱也能够使得特征带有一些非线性的特性，从而提升模型的非线性表达能力。在风控中常用的分箱方法有等频分箱，等距分箱，聚类分箱，卡方分箱，Best-KS分箱等。更加详细的讨论可以参照之前写的文章风控建模中的分箱方法——原理与代码实现。这里使用toda库来实现对特征进行卡方分箱。toad是由厚本金融风控团队内部孵化，后开源并坚持维护的标准化评分卡库。其功能全面、性能稳健、运行速度快，是风控建模中常使用的一个模型开发库。有关toad库的基本使用可以参考下面几篇文章。

Zain Mei：Toad | Pyhon评分卡工具轻松实现风控模型开发168 赞同 · 32 评论文章​编辑

评分卡建模Toad库的使用_Labryant的博客-CSDN博客_python toad库​blog.csdn.net/lc434699300/article/details/105232380​编辑

promise：信贷评分卡建模库Toad简单应用12 赞同 · 1 评论文章​编辑

import toad
combiner = toad.transform.Combiner()
#以训练集拟合得出分箱节点
combiner.fit(train,train["SeriousDlqin2yrs"],method='chi',min_samples=0.05,exclude=["SeriousDlqin2yrs"])
bins = combiner.export()
bins

#按照生成的分箱节点对数据进行分箱处理
train_bin = combiner.transform(train)
valid_bin = combiner.transform(valid)
test_bin = combiner.transform(df_test)
test_bin

分箱转换后每一个特征的值都会被分配一个编号，表示该特征落在某一个分箱中。

分箱的效果可以通过坏客户占比的单调性来进行初步判断以及作为分箱调整的依据。这里坏客户占比的单调性是指在每一个分箱中坏客户的占比是否随着分箱的取值范围的变化而产生单调变化，具体的变化方向需要结合业务知识来考量。这里主要是考虑到业务的可解释性问题，比如对于负债比，理论上负债比越高那么客户的逾期风险也就越高，也就是说，在负债比较高的分箱中坏客户的占比应该是更大的。下面通过绘制Bivar图来观察每个特征分箱后的情况，以便进行适当的分箱调整。

from toad.plot import badrate_plot,bin_plot

for fea in train_bin.columns:
    if fea == 'SeriousDlqin2yrs':
        continue
    bin_plot(frame=train_bin,x=fea,target='SeriousDlqin2yrs',iv=False)

上面展示了几个特征的Bivar图示例，除了DebtRatio外，其他特征基本上满足单调性的要求，其变化方向也与业务上的理解比较接近，比如NumberOfTime30-59DaysPastDueNotWorse（逾期30-59天的次数）增加时，客户最终逾期的风险也在增加。对于DebtRatio，可以通过手动调整分箱节点进行分箱合并，来保障一定的单调性。从图中可以看到第四个分箱坏客户占比下降，不符合整体上升的趋势，因此将其合并到第三个分箱中。

#DebtRatio原先的分箱节点，[0.354411397, 0.49562442100000004, 3.61878453]
#重新设置分箱规则
adj_bin = {'DebtRatio': [0.354411397,0.49562442100000004]}
combiner.set_rules(adj_bin)
#根据新规则重新分箱
train_bin = combiner.transform(train)
valid_bin = combiner.transform(valid)
test_bin = combiner.transform(df_test)
bin_plot(frame=train_bin,x='DebtRatio',target='SeriousDlqin2yrs',iv=False)

重新分箱后可以看到DebtRatio也能够呈现出单调性，随着负债比的增加，客户的逾期风险也在增加，符合业务上的理解。此外，在实际中我们还需要观察一个特征分箱在训练集以及验证集/测试集中的坏客户占比情况以确定分箱是否具有跨时间稳定性。若分箱在训练集上的坏客户占比与验证集/测试集上同一个分箱的坏客户占比差异很大，训练出来的模型不稳定且易过拟合，则需要考虑进行重新分箱。以DebtRatio的负样本关联图来进行说明

#标识样本是训练样本还是验证样本
train_bin['sample_type'] = ['train'] * len(train_bin)
valid_bin['sample_type'] = ['valid'] * len(valid_bin)
#绘制负样本关联图
badrate_plot(frame=pd.concat([train_bin,valid_bin]),x='sample_type',target='SeriousDlqin2yrs',by='DebtRatio')

train_bin= train_bin.drop(columns=['sample_type'])
valid_bin = valid_bin.drop(columns=['sample_type'])

上图每一条线代表的是一个分箱在两个数据集中坏客户占比的连线。这里三个分箱（三条线）没有出现交叉，表明同一个分箱中坏客户占比在两个数据集上的差异不大。若出现交叉，假设上图的0和1出现交叉，意味着这两个分箱中坏客户占比在不同的数据集中差异很大，可以考虑将0和1进行合并。使得分箱中的坏客户占比在训练集和验证集上较为接近。

特征分箱后需要面临的一个问题是分箱的编码。前面也展示过分箱后每一个特征的值都会被赋予一个分箱的编号。这个编号只是对分箱的一种简单编码形式。这种编码无法定量地反映分箱内的样本占比情况。我们习惯以线性的方式来判断变量的作用，即x越大时，y就越大或越小。WOE编码就是通过对比分箱内的坏好客户的占比跟总体的坏好客户占比来衡量分箱对于预测结果的“贡献”。对于这种“贡献”，可以这么去理解。我们为了预测样本是好客户还是坏客户，需要知道一些信息或者说收集一些证据（特征），那么当这些信息非常有用时（特征的一个分箱内几乎全是坏客户），也就是当样本的该特征落在这个分箱时，我们能够很有把握地认为该样本是坏客户。这个证据显然非常重要，那就需要为它赋予一个更大的权重，且这个权重对于预测样本为坏客户起到正向作用。总的来说，WOE的绝对值越大，表示分箱内的样本分布与总体的样本分布差异越大，我们能够从分箱的角度来区分好坏样本。而正负则表示这种差异的方向，即更容易认为分箱内的样本是好样本还是坏样本。下面是每个分箱的WOE值的计算方法，有兴趣进一步了解可以参照之前的文章风控建模指标PSI，IV和WOE理解。使用Toad库的WOETransformer()可以很方便地将分箱后的数据转换为WOE编码。

#对分箱结果进行WOE编码
woe_t = toad.transform.WOETransformer()
train_woe = woe_t.fit_transform(train_bin,train_bin['SeriousDlqin2yrs'],exclude=["SeriousDlqin2yrs"])
valid_woe = woe_t.transform(valid_bin)
test_woe = woe_t.transform(test_bin)
train_woe

4. 特征筛选

一般而言，我们在建模前期根据业务理解以及其他先验知识或现有数据情况可能选择了非常多的特征。但并不意味这些特征都是需要进入模型训练。一方面这些特征有些可能并没有重要的业务指导意义，另一方面，当模型纳入过多特征时，容易使得模型变得复杂，有出现过拟合的风险。当然，本案例中的特征数量不多，且基本上都有重要的业务含义，基本不涉及特征筛选。但为了整个建模流程能够完整，下面还是对特征进行筛选，重点在于理解筛选的流程以及背后的含义。

在建模的过程中，对于一个特征的考量主要考虑几个方面，即特征的稳定性（细微变化不应当引起预测结果的显著变化），特征的可解释性（符合业务理解），特征的预测能力（有效区分好坏客户）。所以，在进行特征筛选的过程中同样是遵循这几项原则，有目的地筛选最终用于模型训练的特征。在本案例中，特征的可解释性基本上是满足的，每一个特征的含义在特征解释部分已经给出。后面主要是从特征的稳定性以及特征的预测能力两个方面来进行筛选。

1）通过IV（Information Value）值确定特征的预测能力

经过WOE编码后的特征被赋予了一个代表特征预测能力的权重，即WOE值（各个分箱WOE值的求和）。但一般我们并不根据WOE来进行特征筛选。一个重要的原因是WOE值并不考虑分箱内样本在总体样本中的占比情况。也就是说，当一个分箱的样本占比很低时，尽管其WOE值很高（里面大部分是坏客户或好客户），但本身样本落在这个分箱的概率就非常小，所以该分箱对于整体样本的预测贡献是不大的。而IV值弥补了这一缺陷，其是分箱WOE值的加权求和。这里的权重就是分箱内坏客户以及好客户在各自总体中的占比情况，也就是考虑了前面所提到的分箱中样本占总体的情况。当分箱中的样本很少时，这个权重也会非常小，此时就算分箱的WOE值很高，最终加权求和的结果也会很低。下面是IV的计算公式以及不同取值的业务含义。

下面使用Toad的quality()函数来计算每个特征的IV值，并过滤掉IV小于0.1的特征。

IV = toad.quality(train_woe,'SeriousDlqin2yrs',iv_only=True).loc[:,'iv'].round(2)
IV

可以看到RevolvingUtilizationOfUnsecuredLines，NumberOfTimes90DaysLate，NumberOfTime30-59DaysPastDueNotWorse，age四个特征的IV值大于0.1，因此予以保留。

2）通过PSI（Population Stability Index）衡量特征的跨时间稳定性

在风控建模中，稳定性甚至比准确性更重要。这里的稳定性是模型评分或特征分箱在不同的数据集（一般认为是训练数据和跨时间验证集）上的分布差异。PSI是衡量模型或特征跨时间稳定性的一个重要指标。在机器学习建模的过程中，一个基本的假设是“历史样本的分布与未来样本的分布一致”，这样我们才有可能利用历史样本来训练模型并应用在未来的样本上。但是，随着时间的推移，客群的属性难免会发生一些细微的变化。如果一个模型或特征是稳定的，那么这种细微的变化不应当引起模型的评分或特征的人群分布产生太大的变化。所以，当模型评分或者特征分箱中的样本占比分布在训练样本上的预期分布跟验证数据上的实际分布差异小，则认为模型或特征足够稳定，其能够在不同的数据集上有相似的表现。我们将随机拆分出来的验证集假设为是跨时间的样本。特征的PSI就是要衡量一个特征在训练集和验证集上的分布差异，如果这种差异很小（PSI小），则表明这个特征是稳定的，不会因为时间的推移（特征发生细微变化）而使得人群产生非常大的变化。有关PSI的详细讨论可以参照之前的文章风控建模指标PSI，IV和WOE理解。下面是PSI的计算公式以及不同取值的业务含义

使用Toda的PSI()函数可以很方便地计算特征的PSI值。根据PSI大于0.25来过滤不稳定的特征。

#计算PSI
psi = toad.metrics.PSI(train_woe,valid_woe)
psi

可以看到前面根据IV值筛选出的四个特征的PSI都小于0.1，所以不需要进一步过滤。

2.3 评分卡建模

1. 生成最终的数据集

根据数据预处理阶段得到的结果，我们完成了对数据的异常过滤和缺失数据插补，完成了特征的分箱，WOE编码以及根据IV和PSI进行特征的筛选。最终模型使用四个特征来进行训练，包括RevolvingUtilizationOfUnsecuredLines，NumberOfTimes90DaysLate，NumberOfTime30-59DaysPastDueNotWorse，age这四个特征。根据这个结果，确定最终用于模型训练和验证的数据集。

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score,roc_curve
import xgboost as xgb
#确定最终用于模型训练和验证的数据集
train_set = train_woe[['RevolvingUtilizationOfUnsecuredLines',
                      'NumberOfTimes90DaysLate','NumberOfTime30-59DaysPastDueNotWorse','age','SeriousDlqin2yrs']] 
valid_set = valid_woe[train_set.columns]
test_set = test_woe[train_set.columns]
#特征以及目标变量
fea_lst = ['RevolvingUtilizationOfUnsecuredLines', 'NumberOfTimes90DaysLate','NumberOfTime30-59DaysPastDueNotWorse','age']
target = 'SeriousDlqin2yrs'

2. 模型选择

机器学习模型有很多，尽管目前XGBoost，神经网络等模型效果更好。但在风控建模中最常用的还是逻辑回归模型。主要是因为逻辑回归模型简单易用，可解释性强。当模型出现问题时，能够更加容易找到原因，各个特征的系数也能够结合业务知识来进行评估和解释。然而，逻辑回归对于非线性问题的处理能力较差。所以，在建模阶段可以同时建立一个更为复杂的辅助模型，如XGBoost。通过观察逻辑回归和辅助模型的模型表现，来进一步调整用于逻辑回归训练的特征。比如，假设下图是XGBoost生成的一个决策过程。那么客户年龄以及负债比就可在组合成一个新的特征。如年龄大于25岁且负债比大于1作为一个组合特征，若客户满足这一情况则标记该特征为1，否则标记为0。同样地，年龄大于25岁且负债比小于1作为一个组合特征，若客户满足这一情况则标记该特征为1，否则标记为0。这就根据XGBoost这种复杂模型生成的一些规则来交叉组合形成一些新的特征，从而使得逻辑回归模型也能够像XGBoost一样具有处理非线性问题的能力，提升逻辑回归的性能

3. 模型评估

 

在我们的评分卡建模中，最终使用AUC和KS来进行模型的评估。

3. 预训练模型

预训练模型的作用在于优化和调整用于模型训练的特征或模型超参数。即利用训练集进行模型训练，在验证集上进行一系列的评估。根据评估结果选择最佳的模型超参数或重新去调整特征。下面将通过建立辅助模型XGBoot来观察是否有必要进行特征的交叉。另一方面，通过正向和方向训练验证的方法来观察是否需要对特征进行调整。这里正向的意思是以训练集训练模型，以验证集评估模型，反向则是反过来，以验证集来训练模型。通过观察正向和反向的评估结果，如果差异较大，则可能代表模型的稳定性很差或训练集和验证集的差异很大，需要对特征进一步调整优化以过滤掉一些不稳定的特征或重新制定划分数据集的策略。

定义逻辑回归模型

def lr_model(x, y, valx, valy, C):  
    model = LogisticRegression(C=C, class_weight='balanced')      
    model.fit(x,y)  
      

    y_pred = model.predict_proba(x)[:,1]  
    fpr_dev,tpr_dev,_ = roc_curve(y, y_pred)  
    train_ks = abs(fpr_dev - tpr_dev).max()
    dev_auc = roc_auc_score(y_score=y_pred,y_true=y)
    print('train_ks : ', train_ks)  

    y_pred = model.predict_proba(valx)[:,1]  
    fpr_val,tpr_val,_ = roc_curve(valy, y_pred)  
    val_ks = abs(fpr_val - tpr_val).max()
    val_auc = roc_auc_score(y_score=y_pred,y_true=valy)
    print('val_ks : ', val_ks)  
    
    plt.plot(fpr_dev, tpr_dev, label='dev:{:.3f}'.format(dev_auc))  
    plt.plot(fpr_val, tpr_val, label='val:{:.3f}'.format(val_auc))  
    plt.plot([0,1], [0,1], 'k--')  
    plt.xlabel('False positive rate')  
    plt.ylabel('True positive rate')  
    plt.title('ROC Curve')  
    plt.legend(loc='best')  
    plt.show() 

定义XGBoost模型

def xgb_model(x, y, valx, valy):  
    model = xgb.XGBClassifier(learning_rate=0.05,  
                              n_estimators=400,  
                              max_depth=2,  
                              min_child_weight=1,  
                              subsample=1,   
                              nthread=-1,  
                              scale_pos_weight=1,  
                              random_state=1,  
                              n_jobs=-1,  
                              reg_lambda=300,
                              use_label_encoder=False)  
    model.fit(x, y,eval_metric='logloss')  
     
    y_pred = model.predict_proba(x)[:,1]  
    fpr_dev,tpr_dev,_ = roc_curve(y, y_pred)  
    train_ks = abs(fpr_dev - tpr_dev).max()  
    dev_auc = roc_auc_score(y_score=y_pred,y_true=y)
    print('train_ks : ', train_ks)  

    y_pred = model.predict_proba(valx)[:,1]  
    fpr_val,tpr_val,_ = roc_curve(valy, y_pred)  
    val_ks = abs(fpr_val - tpr_val).max()  
    val_auc = roc_auc_score(y_score=y_pred,y_true=valy)
    print('val_ks : ', val_ks)  
    plt.plot(fpr_dev, tpr_dev, label='dev:{:.3f}'.format(dev_auc))  
    plt.plot(fpr_val, tpr_val, label='val:{:.3f}'.format(val_auc))  
    plt.plot([0,1], [0,1], 'k--')  
    plt.xlabel('False positive rate')  
    plt.ylabel('True positive rate')  
    plt.title('ROC Curve')  
    plt.legend(loc='best')  
    plt.show()  

定义函数调用模型

def bi_train():
    train_x,train_y = train_set[fea_lst],train_set[target]
    valid_x,valid_y = valid_set[fea_lst],valid_set[target]
    test_x = test_set[fea_lst]
    print("正向逻辑回归")
    lr_model(x=train_x,y=train_y,valx=valid_x,valy=valid_y,C=0.1)
    print("反向向逻辑回归")
    lr_model(x= valid_x,y=valid_y,valx=train_x,valy=train_y,C=0.1)
    print("XGBoost")
    xgb_model(x=train_x,y=train_y,valx=valid_x,valy=valid_y)
 
bi_train()

从正向和反向逻辑回归的结果来看，模型的性能并没有很大的差异。在正向模型中，验证集上的AUC为0.836，KS为0.53。模型表现出良好的性能。而在反向模型中，验证集（即正向中的训练集）上的AUC为0.845，KS为0.54。与正向模型相比，KS差异不超过5%，因此模型足够稳定，不需要调整数据集或过滤不稳定的特征。从XGBoost的性能评估结果来看，其AUC为0.847，与正向模型中0.836相比并没有显著的提升。因此，当前使用的特征不需要进行交叉组合来提升模型的非线性能力。

4. 模型训练

经过预训练过程的分析后，当前的数据集以及特征基本上不需要进行改动，因此将训练集与验证集合并重新训练模型，作为最终的评分卡模型。

经过预训练过程的分析后，当前的数据集以及特征基本上不需要进行改动，因此将训练集与验证集合并重新训练模型，作为最终的评分卡模型。

model = LogisticRegression(C=0.1, class_weight='balanced')
all_train = pd.concat([train_set,valid_set],axis=0)
model.fit(all_train[fea_lst],all_train[target])
#在测试集上预测标签
pro = model.predict_proba(test_set[fea_lst])[:,1]

至此，我们已经完成了模型的训练和评估。由于这里使用的测试集是没有标签的，因此无法评估最终模型在测试集上的表现。在实际建模中，需要重新评估模型在测试集上的性能。同样包括AUC，F1，KS等。此外，也需要评估模型在训练集和测试集上的PSI，以验证模型的稳定性。

2.4 评分卡生成

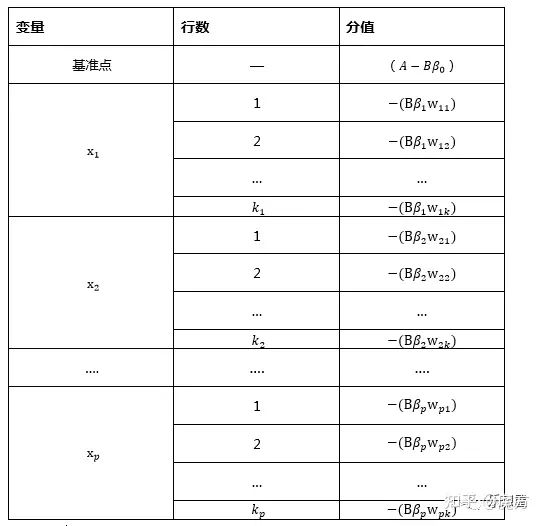
在第一部分的信用评分卡介绍中我们看到，实际应用的评分卡应当是是一张有分数刻度和相应阈值的表。逻辑回归的输出是一个概率，即该样本是坏客户的概率。因此，我们需要将这种概率进行转换，形成一个分数。这就是评分卡建模的最后一步，即评分卡的生成。

对于评分卡的生成原理，我们先从感性的角度来理解。首先，最终的评分应当是每个特征的得分的总和，这样才能体现出每个特征的贡献。另一方面，评分应当随着预测风险的增加或降低来相应地降分或加分。并且增加或减少多少分应该有一个固定的映射关系，这个映射关系要与模型初始输出的概率p有关。这样我们才能够根据不同评分的差异来量化这个风险变化的大小。那么，逻辑回归中有哪些地方可以涵盖这两个方面呢？那就是对数几率。在逻辑回归中有如下关系。

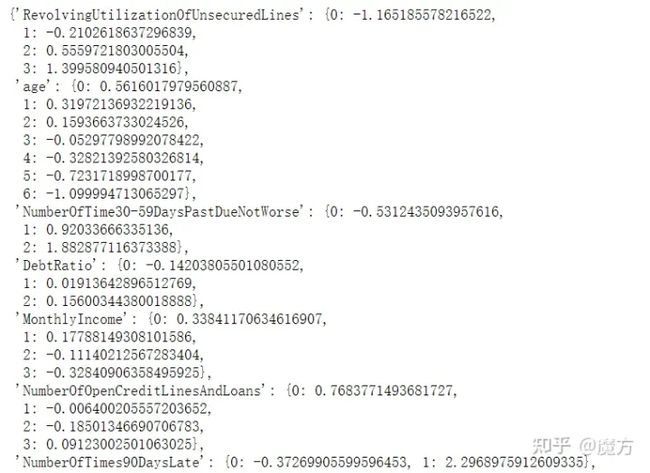
#woe的编码规则
woe_map = woe_t.export()
woe_map

#得到特征，分箱编号以及分箱woe值的表
woe_df = []
for f in fea_lst:
    woes = woe_map.get(f)
    for b in woes.keys():
        woe_df.append([f,b,woes.get(b)])
woe_df = pd.DataFrame(columns=['feature','bins','woe'],data=woe_df)
woe_df

#生成分箱区间
bins = combiner.export()
bin_df = []
for fea in fea_lst:
    f_cut = bins.get(fea)
    f_cut = [float('-inf')] + f_cut + [float('inf')]
    for i in range(len(f_cut)-1):
        bin_df.append([fea,i,pd.Interval(f_cut[i],f_cut[i+1])])
bin_df = pd.DataFrame(columns=['feature','bins','interval'],data=bin_df)
bin_df

#生成评分卡
score_df = pd.merge(woe_df,bin_df,on=['feature','bins'])[['feature','interval','woe']]
coef = model.coef_
#每个特征的分箱数
bins_num = [len(bins.get(i))+1 for i in fea_lst]
coef = np.repeat(coef,bins_num).
#模型拟合出来的参数
score_df['coef'] = coef

'''
设定Odds为20:1时基准分600分，放Odds增加2倍时分数减50，即PDO=50
'''
factor = round(50 / np.log(2),0)
offset = round(600 + factor * np.log(20),0)
#BasicScore,即评分公式中的常数部分
basic_score = round(offset - factor * model.intercept_[0],0)

score_df['score'] = (-factor * score_df['coef']*score_df['woe']).round(0)
card = score_df[['feature','interval','score']]
#将基准分加上
card = card.append({'feature':'basic_score','interval':np.nan,'score':basic_score},ignore_index=True)
card

至此，我们已经成功生成了信用评分卡，后续使用时，可以按照评分卡定义的分数刻度和阈值，根据客户的属性来得到最终的得分。

2.5 验证评分卡的有效性

这里可以根据前面生成的评分卡写一个映射函数，当传入一个客户样本是自动计算出得分，最后来对比好坏客户的得分差异，如果坏客户的得分小于好客户的得分那么表明评分卡是有效的。

#评分映射函数
def map_score(customer):
    score = []
    for i in customer.index:
        #一个特征的计分区间
        fea_score = card[card['feature']==i]
        for _,row in fea_score.iterrows():
            #card中的interval列类型是pd.Interval，直接用in来判断是否在区间内
            if customer.loc[i] in row['interval']:
                score.append(row['score'])
                break
    score = sum(score) + card[card['feature']=='basic_score']['score']
    return score.values[0]

#随机选择相同数量的好客户和坏客户
verify_bad = all_train[all_train[target]==1].sample(frac=0.3)
verify_good = all_train[all_train[target]==0].sample(n=len(verify_bad))

bad_scores = []
good_scores = []
#计算坏客户的得分
for _, customer in verify_bad.iterrows():
    s = map_score(customer.loc[fea_lst])
    bad_scores.append(s)
#计算好客户的得分   
for _, customer in verify_good.iterrows():
    s = map_score(customer.loc[fea_lst])
    good_scores.append(s)

ver_score_df = pd.DataFrame(columns=['bad','good'],data=np.array([bad_scores,good_scores]).T)
print("好客户得分均值:{:.2f}\n坏客户得分均值:{:.2f}".format(ver_score_df['good'].mean(),ver_score_df['bad'].mean()))
_,pv = ttest_ind(ver_score_df['bad'],ver_score_df['good'],equal_var=False)
print("pvalue:",pv)

从结果中可以看到坏客户的得分均值小于好客户得分，且差异具有统计意义（p值小于0.001）。表明我们生成 的评分卡是有效的，对于坏客户的确会得到一个低的评分。

3. 总结

本文从信用卡评分的基础概念开始，理解信用评分卡在风控中发挥的作用。第二部分使用公开的信用数据集从0到1建立了一个信用评分卡。包括数据的探索性分析，数据预处理，评分卡建模，评分卡生成以及最后的有效性验证。在建模过程中也交叉地介绍了一些理论概念，这也有助于理解每一个步骤具体含义。整体上梳理了风控中信用评分卡的建模流程。