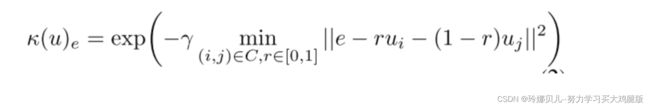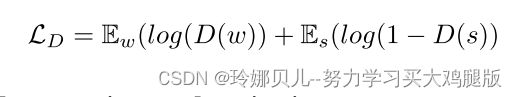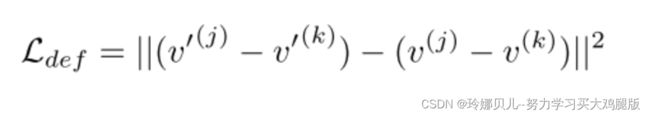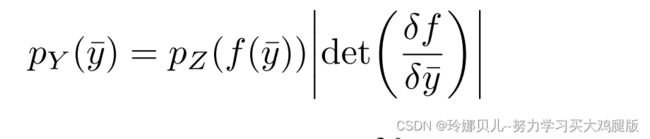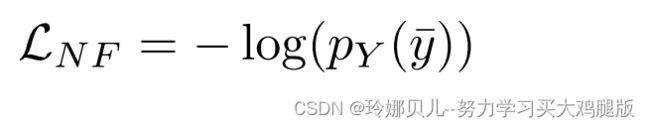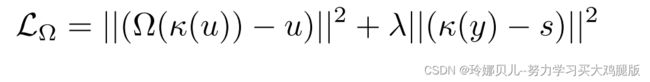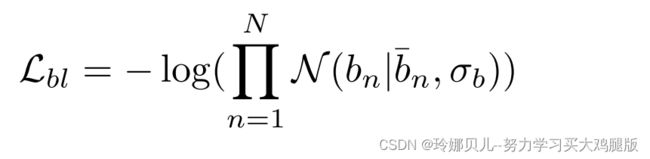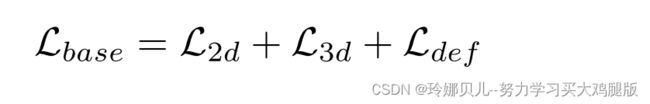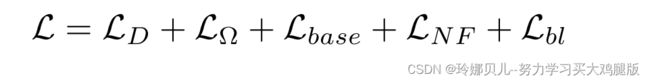Self-supervised 3D Human Pose Estimation from a Single Image

基于单幅图像的自监督三维人体姿态估计

 

主页： https://josesosajs.github.io/ imagepose/

源码：未开源

摘要

我们提出了一种新的自我监督的方法预测三维人体姿势从一个单一的图像。预测网络是从描绘处于典型姿势的人的未标记图像的数据集和一组未配对的2D姿势训练的。通过最小化对注释数据的需要，该方法具有快速应用于其他铰接结构（例如，关节）的姿态估计的潜力。动物）。自我监督来自早期的想法，利用3D旋转下的预测姿势之间的一致性。我们的方法是一个实质性的进步，在国家的最先进的自我监督的方法，直接从图像中训练映射，没有肢体关节的约束或任何3D经验的姿态之前。我们使用提供图像和地面真实3D姿势的基准数据集（Human3.6M，MPI-INF-3DHP）将性能与最先进的自监督方法进行比较。尽管对注释数据的要求降低，但我们表明该方法优于Human3.6M，并与MPI-INF-3DHP的性能相匹配。定性结果的数据集ofhuman手显示的潜力，快速学习，以预测3D姿态关节结构以外的人体。

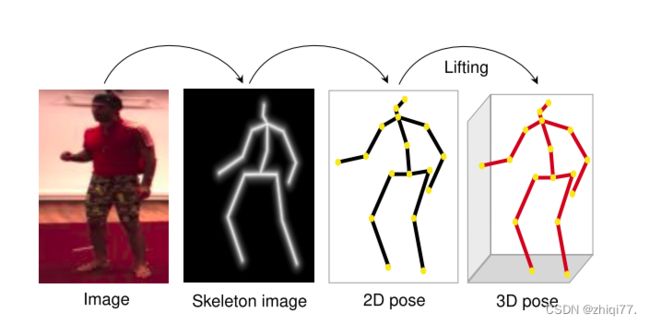
 3D姿态估计流水线。我们的方法通过2D姿态的中间表示联合学习从图像中估计3D姿态。管道嵌入在更大的网络中，用于端到端训练。

引言

我们的方法同时学习2D和3D姿态表示在很大程度上是无监督的方式，只需要一个经验先验的未配对的2D姿势。我们在Human3.6M [11]和MPI-INF 3DHP [23]数据集上证明了其有效性，这是两个最受欢迎的人体姿势估计基准。我们还使用人手的合成数据集显示了该方法对其他关节结构的适应性[33]。在实验中，该方法优于最先进的自监督方法，这些方法从图像中估计3D姿态，并且在训练中需要更高的监督。总的来说，我们的方法具有以下优点：

它不假设任何3D姿势注释或配对的2D姿势注释。

它具有快速适应其他铰接结构（例如，关节）的3D姿态预测的潜力。动物和有关节的无生命物体）。

方法

我们提出的3D姿态估计模型由从全身图像映射到3D姿态的三个网络Φ、Ω、Λ的流水线组成。这在图2中左上角的蓝色虚线框中显示。管道包括：

- 从输入图像X映射到中间骨架图像s的卷积神经网络（CNN）Φ

- 从s到2D姿态表示y的第二CNN Ω映射

- 完全连接的网络Λ将2D姿态y提升到所需的3D姿态V

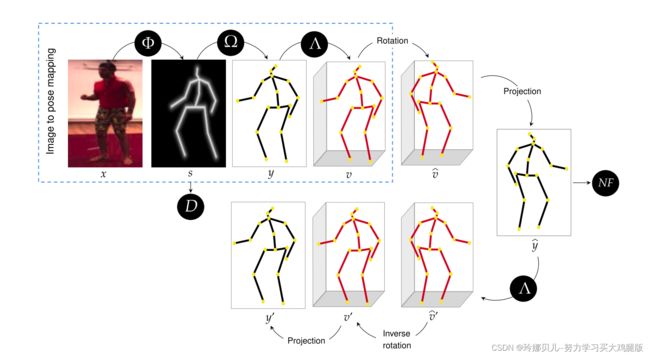图2

 

我们通过将这三个网络合并到一个更大的网络（图2）来一起训练它们，并优化端到端。该更大的网络被构造成并入3D姿态的变换的循环。环周围的几何一致性的程度有助于损失函数，并提供训练的自我监督。训练从描绘不同姿势的人的图像数据集开始。我们还假设我们有一个典型的2D姿态的（通常不相关的）数据集，我们使用可微渲染函数κ从该数据集获得骨架图像。这些将在GAN框架D中使用，以帮助确保生成的骨架图像是真实的。在下面的章节中，我们将提供有关模型组件的更多详细信息。

Image to 3D pose mapping

图像到姿态映射是网络Φ、Ω、Λ的组成，以将示出人的图像X映射到其3D姿态表示V。映射的第一部分是CNN Φ，它从图像x映射到骨架图像s = Φ（x），将人显示为简笔画。我们的网络Φ采用与[14]中的自动编码器类似的架构，但没有解码器级。经过训练后，s中出现的骨架与x中的人对齐。

然后，网络Ω将骨架图像s映射到2D姿态表示y = Ω（Φ（x））。非正式地，Ω学习从骨架图像中提取2D关节位置（xi，yi）。最后，Λ是将2D姿态提升到3D中的所需姿态V的神经网络。特别地，Λ（y）估计输入y中的每对（xi，yi）关节位置的深度zi = di + Δ，其中Δ是恒定深度。然后，关节vi在3D姿态V中的3D位置由下式给出：

 

 其中Zi被强制为大于1，以防止来自负深度的不确定性。与以前的作品[3，38，41]一致，∆固定为10。

我们的提升网络Λ是基于[3，22]的工作，并在[38]之后扩展。在这种情况下，我们的扩展版本不仅输出输入中每个关节位置（xi，yi）的深度zi，还生成仰角α的值。当执行3D姿势V的旋转时，将使用该角度。特别地，我们使用α来固定垂直轴相对于执行旋转的地平面的仰角。

总结

 Skeleton images and discriminator

骨架图像和鉴别器

我们鼓励训练网络生成逼真的骨架图像的帮助下，经验的2D姿势。注意，这些2D姿态是未配对的，即，它们不是训练图像的注释。首先使用[14]提出的渲染器将来自我们的经验先验的2D姿态渲染为骨架图像。令C是一组连接的关节对（i，j），e是图像像素位置，并且u是身体关节位置的一组（x，y）2D坐标。骨架图像渲染函数由下式给出：

非正式地，κ通过从链接关节的线段定义距离场来工作，并应用指数衰减来创建图像。 

由[14]，我们使用鉴别器网络D，其使用先前骨骼图像来鼓励预测的骨骼图像表示可信的姿势。D的任务是确定骨架图像s = Φ（x）是否看起来像真实的骨架图像，例如先前w = κ（u）中的那些。形式上，目标是学习D（s）∈ [0，1]以匹配骨架图像的参考分布p（w）和预测骨架图像的分布q（s）。对抗性损失[8]比较未配对样本w和预测s：

 Random rotations and projections

随机旋转和投影

我们的模型的基本组成部分是提升过程，其允许从估计的2D输入y学习准确的3D姿态V。为了提供提升函数和最终整个端到端网络的自我监督，我们通过随机旋转三维姿态v的第二个虚拟视图（v = R * v）来模拟三维姿态v的虚拟视图。以前的工作[3]已经通过从固定分布均匀地采样方位角和仰角来选择旋转矩阵R。最近，[38]证明了学习仰角分布会导致更好的结果。因此，我们遵循他们的方法并使用Λ来预测旋转矩阵的仰角。围绕方位轴Ra的旋转从均匀分布[-π，π]采样。

根据[38]，我们还通过计算分批平均值µe和标准差σe来预测数据集的仰角Re正态分布。我们从正态分布N（µe，σe）中采样，以在仰角方向Re上旋转姿态。然后，完整的旋转矩阵R由给出。

在旋转3D姿势之后，我们通过透视投影投影来投影v。然后，相同的提升网络Λ（y）产生另一个3D姿态（v’，其然后旋转回到原始视图。使用相同的透视投影将最终3D姿势v’投影到2D。3D姿势的变换的该循环提供了自我监督的一致性损失。在此上下文中，我们假设如果提升网络Λ准确地估计2D输入y的深度，则3D姿态（v）和（v’应该是相似的。相同的原理适用于y和最终2D投影y’。这给出了损失函数的以下两个分量：

此外，3D姿势v和v’应该是相似的。然而，我们不是与L2损失进行比较，而是遵循[38，41]并测量来自网络中相应阶段的批次的两个样本之间的3D姿态差异的变化。

 

 类似于Wandt et al.[38]，我们不假设样本来自相同的视频序列;样本j和k可以来自不同的序列和对象。

总结

 ，由预测，从均匀分布[-π，π]采样。由数据集的均值方差求来，从正态分布N（µe，σe）中采样。实现自我监督

Empirical prior on 2D pose

LikeWandt等人[38]，我们使用归一化流来提供2D姿势的先验。归一化流将简单分布（例如，正态分布）转换成复分布，使得可以容易地计算在该复分布下的样本密度。设Z ∈ RN为正态分布，g为可逆函数g（z）= ¯y，其中¯y ∈ RN为二维人体姿态向量y在PCA子空间中的投影。通过改变变量，y的概率密度函数由下式给出：

其中f是g的倒数，det中是雅可比矩阵。在[38]中的归一化流程实现之后，我们将f表示为神经网络[4]，并在具有负对数似然损失的2D姿态数据集上进行优化： 

 

Additional losses

我们计算从骨骼图像到2D姿态的映射的损失y = Ω（s）。我们使用与[14]相同的损失，但没有预训练Ω，即，我们与所有其他网络同时学习这种映射。LΩ由下式给出

其中u表示来自未配对先验的2D姿态，s是预测的骨架图像，并且λ是设置为0.1的平衡系数。函数κ是骨架图像渲染器。 

基于将相对骨长度并入姿态估计方法[21，28，38]的已证明的有效性，我们添加该方法以在估计3D姿态时施加软约束。按照[38]中的公式，我们计算第n个骨骼的相对骨骼长度bn除以给定姿势v的所有骨骼的平均值。我们使用预先计算的相对骨骼长度作为高斯先验的平均值。然后，骨长度的负对数似然定义损失函数

 其中，N是由关节之间的连接性定义的骨骼数量。请注意，这是一个软约束，允许个体之间的相对骨长度变化。

Training

我们从头开始训练Φ、Ω、D和Λ。如[38]所示，只有归一化流是独立预训练的。用于训练我们的模型的完整损耗函数具有七个分量，为了便于消融研究，我们将这些损失项中的三个分组并将其表示为Lbase

因此，最终的复合损失函数被定义为：

 

 在测试期间，我们只保留由图2左上方框中所示的训练Φ、Ω和Λ网络组成的流水线。关于网络和培训的更详细说明，请参见补充部分。