边界框回归的魔法：揭秘精准高效的MPDIoU损失函数

摘要

https://arxiv.org/pdf/2307.07662.pdf
边界框回归（BBR）已广泛应用于目标检测和实例分割，这是目标定位的重要步骤。然而，现有的大多数边界框回归损失函数在预测框与地面真相框具有相同长宽比但宽度和高度值完全不同的情况下无法优化。为了解决上述问题，我们充分探索了水平矩形的几何特征，并基于最小点距离提出了一种新颖的边界框相似性比较度量MPDIoU，该度量包含了现有损失函数中考虑的所有相关因素，即重叠或非重叠区域、中心点距离以及宽度和高度偏差，同时简化了计算过程。在此基础上，我们提出了基于MPDIoU的边界框回归损失函数${\text{L}}_{\text{MPDIoU}}$。实验结果表明，将MPDIoU损失函数应用于在PASCAL VOC、MS COCO和IIIT5k上训练的现有最先进实例分割（例如YOLACT）和目标检测（例如YOLOv7）模型，其性能优于现有损失函数。

关键词：目标检测、实例分割、边界框回归、损失函数

1、简介

目标检测和实例分割是计算机视觉领域的两个重要问题，在过去的几年里吸引了大量研究者的兴趣。大多数最先进的目标检测器（例如，YOLO系列[1,2,3,4,5,6]，Mask R-CNN[7]，Dynamic R-CNN[8]和DETR[9]）都依赖于边界框回归（BBR）模块来确定物体的位置。基于这个范式，一个精心设计的损失函数对于BBR的成功至关重要。到目前为止，大多数现有的BBR损失函数分为两类：${\ell }_n$范数损失函数和交并比（IoU）损失函数。

然而，现有的大多数用于边界框回归的损失函数在相同预测结果下具有相同的值，这降低了边界框回归的收敛速度和准确性。因此，考虑到现有用于边界框回归的损失函数的优点和缺点，受水平矩形几何特征的启发，我们尝试设计一种基于最小点距离的用于边界框回归的新型损失函数LMPDIoU，并在边界框回归过程中使用MPDIoU作为一种新措施来比较预测边界框与地面真实边界框之间的相似性。我们还提供了一种易于实现的解决方案，用于计算两个轴对齐矩形之间的MPDIoU，使其可以作为评估指标将MPDIoU纳入最先进的目标检测和实例分割算法中，并且在PASCAL VOC [10]，MS COCO [11]，IIIT5k [12]和MTHv2 [13]等一些主流目标检测，场景文本检测和实例分割数据集上进行了测试，以验证我们提出的MPDIoU的性能。

本文的贡献可以概括如下：

• 1.我们考虑了现有IoU损失和${\ell }_n$范数损失的优点和缺点，然后提出了基于最小点距离的IoU损失，称为${\mathcal{L}}_{MPDIoU}$，以解决现有损失的问题，并获得更快的收敛速度和更准确的回归结果。
• 2.在目标检测、字符级场景文本检测和实例分割任务上进行了广泛的实验。优秀的实验结果验证了所提出的MPD IoU损失的优越性。详细的消融研究展示了不同损失函数和参数值的设置效果。

2、相关工作

2.1、目标检测和实例分割

在过去的几年中，来自不同国家和地区的许多研究人员提出了大量的基于深度学习的目标检测和实例分割方法。总的来说，边界框回归已被许多代表性的目标检测和实例分割框架采用作为基本组件[14]。在用于目标检测的深度模型中，R-CNN系列[15][16][17]采用两个或三个边界框回归模块来获得更高的定位精度，而YOLO系列[2][3][6]和SSD系列[18][19][20]采用一个来获得更快的推理。RepPoints[21]预测几个点来定义一个矩形框。FCOS[22]通过预测采样点到地面真实边界框的顶部、底部、左侧和右侧的欧几里得距离来定位对象。

例如，对于实例分割，PolarMask [23]在n个方向上预测从采样点到物体边缘的射线的长度，以分割实例。还有其他检测器，例如RRPN [24]和R2CNN [25]，通过添加旋转角度回归以检测任意定向的目标，用于遥感检测和场景文本检测。Mask R-CNN [7]在Faster R-CNN [15]上添加了一个额外的实例掩码分支，而最近的state-of-the-art YOLACT [26]在RetinaNet [27]上也做了同样的事情。总之，边界框回归是用于目标检测和实例分割的最新深度模型的关键组件之一。

2.2. 场景文本识别

为了解决任意形状场景文本检测和识别的问题，ABCNet[28]及其改进版本ABCNet v2[29]使用BezierAlign将任意形状的文本转换为规则形状。这些方法通过使用校正模块将检测和识别统一为端到端可训练的系统，取得了很大进展。［30］提出RoI Masking以提取任意形状文本识别的特征。类似于［30，31］尝试使用更快的检测器进行场景文本检测。AE TextSpotter［32］使用识别结果通过语言模型来指导检测。受［33］的启发，[34]提出了一种基于变换器的场景文本检测方法，该方法提供了实例级文本分割结果。

2.3、边界框回归的损失函数

起初，${\ell }_n$范数损失函数被广泛用于边界框回归，它非常简单但对各种尺度都很敏感。在YOLO v1[35]中，对w和h采用平方根以减轻这种影响，而YOLO v3[2]使用$2\times wh$。为了更好地计算地面真实边界框和预测边界框之间的差异，自Unitbox[36]开始使用IoU损失。为了确保训练稳定性，Bounded-IoU损失[37]引入了IoU的上界。对于训练目标检测和实例分割的深度模型，建议使用基于IoU的度量标准，比${\ell }_n$范数更一致[38,37,39]。原始的IoU表示预测边界框和地面真实边界框的交集面积和并集面积的比率（如图1(a)所示），可以表示为
$$IoU=\frac{{\mathcal{B}}_{gt}\cap {\mathcal{B}}_{prd}}{{\mathcal{B}}_{gt}\cup {\mathcal{B}}_{prd}},\text{\hspace{1em}(1)}$$
其中，${\text{B}}_{gt}$表示groundtruth边界框，${\text{B}}_{prd}$表示预测边界框。可以看到，原始IoU只计算两个边界框的并集面积，无法区分两个框不重叠的情况。如方程1所示，如果$\left|{\text{B}}_{gt}\cap {\text{B}}_{prd}\right|=0$，则$IoU({\text{B}}_{gt},{\text{B}}_{prd})=0$。在这种情况下，IoU无法反映两个框是彼此接近还是相距很远。接着，为了解决这个问题，提出了GIoU [39]。GIoU可以表示为
$$GIoU=IoU-\frac{\left|C-{\mathcal{B}}_{gt}\cup {\mathcal{B}}_{prd}\right|}{|C|},\text{\hspace{1em}(2)}$$
其中，C表示覆盖${\text{B}}_{gt}$和${\text{B}}_{prd}$的最小框（如图1(a)中的黑色虚框所示），$|C|$表示框C的面积。由于GIoU损失中引入了惩罚项，因此即使在不重叠的情况下，预测框也会向目标框移动。GIoU损失已被应用于训练最先进的目标检测器，例如YOLO v3和Faster R-CNN，并且取得了比MSE损失和IoU损失更好的性能。然而，当预测边界框完全被groundtruth边界框覆盖时，GIoU会失去效果。为了解决这个问题，考虑到预测边界框和groundtruth边界框之间的中心点距离，提出了DIoU[40]。DIoU的公式可以表示为
$$DIoU=IoU-\frac{{\rho }^2\left({\mathcal{B}}_{gt},{\mathcal{B}}_{prd}\right)}{C^2}\text{\hspace{1em}(3)}$$

其中，${\rho }^2({\text{B}}_{gt},{\text{B}}_{prd})$表示预测边界框和groundtruth边界框的中心点之间的欧几里得距离（如图1(b)中的红虚线所示）。$C^2$表示最小外接矩形的对角线长度（如图1(b)中的黑虚线所示）。我们可以看到，${\text{L}}_{DIoU}$的目标直接最小化预测边界框的中心点和groundtruth边界框的中心点之间的距离。然而，当预测边界框的中心点和groundtruth边界框的中心点重合时，它会退化为原始IoU。为了解决这个问题，考虑到中心点距离和 aspect ratio，提出了CIoU。CIoU的公式可以写为：

$$CIoU=IoU-\frac{{\rho }^2\left({\mathcal{B}}_{gt},{\mathcal{B}}_{prd}\right)}{C^2}-\alpha V,\text{\hspace{1em}(4)}$$

$$V=\frac{4}{{\pi }^2}{\left(\arctan \frac{w^{gt}}{h^{gt}}-\arctan \frac{w^{prd}}{h^{prd}}\right)}^2,\text{\hspace{1em}(5)}$$

$$\alpha =\frac{V}{1-IoU+V}.\text{\hspace{1em}(6)}$$

但是，CIoU中的 aspect ratio 的定义是相对值而不是绝对值。为了解决这个问题，基于DIoU提出了EIoU [41]，其定义如下：
$$EIoU=DIoU-\frac{{\rho }^2\left(w_{prd},w_{gt}\right)}{{\left(w^c\right)}^2}-\frac{{\rho }^2\left(h_{prd},h_{gt}\right)}{{\left(h^c\right)}^2}\text{\hspace{1em}(7)}$$
然而，如图2所示，上述用于边界框回归的损失函数在预测边界框和groundtruth边界框具有相同的长宽比但宽度和高度值不同的情况下会失去有效性，这将限制收敛速度和准确性。因此，我们尝试设计一种名为${\text{L}}_{MPDIoU}$的新型损失函数用于边界框回归，同时考虑到${\text{L}}_{GIoU}[39]、{\text{L}}_{DIoU}[40]、{\text{L}}_{CIoU}[42]、{\text{L}}_{EIoU}$ [41]等损失函数的优点，但对于边界框回归具有更高的效率和准确性。然而，现有损失函数并没有充分利用边界框回归的几何特性。因此，我们通过最小化预测边界框和groundtruth边界框之间的左上角和右下角点之间的距离来提出MPDIoU损失，以更好地训练目标检测、字符级场景文本检测和实例分割的深度模型。

3、点距最小的并集交点

在分析了上述基于IoU的损失函数的优缺点后，我们开始思考如何提高边界框回归的准确性和效率。一般来说，我们使用左上角和右下角点的坐标来定义一个唯一的矩形。受边界框的几何属性的启发，我们设计了一种名为MPDIoU的新型IoU度量来最小化预测边界框和groundtruth边界框之间的左上角和右下角点之间的距离。MPDIoU的计算总结在算法1中。

总之，我们提出的MPDIoU简化了两个边界框之间的相似性比较，可以适应重叠或非重叠边界框回归。因此，MPDIoU可以成为2D/3D计算机视觉任务中使用的所有性能度量的IoU的适当替代品。本文只关注2D目标检测和实例分割，我们可以很容易地将MPDIoU作为度量和损失。轴对齐3D情况的扩展留作未来的工作。

在训练阶段，通过最小化下面的损失函数迫使模型预测的每个边界框${\text{B}}_{prd}={\left[x^{prd},y^{prd},w^{prd},h^{prd}\right]}^T$接近其groundtruth边界框${\text{B}}_{gt}={\left[x^{gt},y^{gt},w^{gt},h^{gt}\right]}^T$：
$$\mathcal{L}=\underset{\Theta }{\min }\sum _{{\mathcal{B}}_{gt}\in {\mathbb{B}}_{gt}}\mathcal{L}\left({\mathcal{B}}_{gt},{\mathcal{B}}_{prd}\mid \Theta \right)\text{\hspace{1em}(8)}$$

其中，${\text{B}}_{gt}$是groundtruth边界框的集合，$\Theta$是用于回归的深度模型的参数。$\text{L}$的典型形式是\ell_{n}-范数，例如，均方误差（MSE）损失和Smooth-\text{}\ell_{1}损失[43]，这些损失已广泛应用于目标检测[44]，行人检测[45,46]，场景文本检测[34,47]，3D目标检测[48,49]，姿态估计[50,51]和实例分割[52,26]。然而，最近的研究表明，基于${\ell }_n$-范数的损失函数与IoU评估指标不一致，因此提出基于IoU的损失函数[53,37,39]。根据前面一节中MPDIoU的定义，我们定义基于MPDIoU的损失函数如下：
$${\mathcal{L}}_{\text{MPDIoU }}=1-\text{ MPDIoU }\text{\hspace{1em}(9)}$$
因此，现有的边界框回归损失函数的所有因子都可以由四个点坐标确定。换算公式如下:
$$|C|=\left(\max \left(x_2^{gt},x_2^{prd}\right)-\min \left(x_1^{gt},x_1^{prd}\right)\right)\ast \left(\max \left(y_2^{gt},y_2^{prd}\right)-\min \left(y_1^{gt},y_1^{prd}\right)\right),\text{\hspace{1em}(10)}$$

$$x_c^{gt}=\frac{x_1^{gt}+x_2^{gt}}{2},y_c^{gt}=\frac{y_1^{gt}+y_2^{gt}}{2},y_c^{prd}=\frac{y_1^{prd}+y_2^{prd}}{2},x_c^{prd}=\frac{x_1^{prd}+x_2^{prd}}{2},\text{\hspace{1em}(11)}$$

$$w_{gt}=x_2^{gt}-x_1^{gt},h_{gt}=y_2^{gt}-y_1^{gt},w_{prd}=x_2^{prd}-x_1^{prd},h_{prd}=y_2^{prd}-y_1^{prd}.\text{\hspace{1em}(12)}$$
其中，|C|代表包围${\mathcal{B}}_{gt}$和${\mathcal{B}}_{prd}$的最小矩形的面积，$\left(x_c^{gt},y_c^{gt}\right)$和$\left(x_c^{prd},y_c^{prd}\right)$分别代表groundtruth边界框和预测边界框的中心点的坐标，$w_{gt}$和$h_{gt}$代表groundtruth边界框的宽度和高度，$w_{prd}$和$h_{prd}$代表预测边界框的宽度和高度。

根据式(10)-(12)，我们可以发现现有损失函数中考虑的所有因素都可以通过左上角点和右下角点的坐标确定，例如非重叠区域、中心点距离、宽度和高度偏差，这意味着我们提出的${\mathcal{L}}_{MPDIoU}$不仅考虑周全，而且简化了计算过程。

根据定理3.1，如果预测边界框和groundtruth边界框的宽高比相同，则groundtruth边界框内的预测边界框比groundtruth边界框外的预测边界框具有更低的${\mathcal{L}}_{MPDIoU}$值。这一特性确保了边界框回归的准确性，倾向于为预测边界框提供更少的冗余。

定理3.1。我们定义一个groundtruth边界框为${\mathcal{B}}_{\text{gt}}$，两个预测边界框为${\mathcal{B}}_{\text{prd}1}$和${\mathcal{B}}_{\text{prd}2}$。输入图像的宽度和高度分别为w和h。假设${\mathcal{B}}_{gt}$、${\mathcal{B}}_{\text{prd}1}$和${\mathcal{B}}_{\text{prd}2}$的左上角和右下角坐标为$\left(x_1^{gt},y_1^{gt},x_2^{gt},y_2^{gt}\right)$、$\left(x_1^{prd1},y_1^{prd1},x_2^{prd1},y_2^{prd1}\right)$和$\left(x_1^{prd2},y_1^{prd2},x_2^{prd2},y_2^{prd2}\right)$，则${\mathcal{B}}_{gt}$、${\mathcal{B}}_{\text{prd}1}$和${\mathcal{B}}_{\text{prd}2}$的宽度和高度可表示为$\left(w_{gt}=y_2^{gt}-y_1^{gt},h_{gt}=x_2^{gt}-x_1^{gt}\right)$、$\left(w_{prd1}=y_2^{prd1}-y_1^{prd1},h_{prd1}=x_2^{prd1}-x_1^{prd1}\right)$和$\left(w_{prd2}=y_2^{prd2}-y_1^{prd2},h_{prd2}=x_2^{prd2}-x_1^{prd2}\right)$.若$w_{prd1}=k\ast w_{gt}$且$h_{prd1}=k\ast h_{gt}$，$w_{prd2}=\frac{1}{k}\ast w_{gt}$且$h_{prd2}=\frac{1}{k}\ast h_{gt}$，其中$k>1$且$k\in N\ast$。

${\mathcal{B}}_{gt}$、${\mathcal{B}}_{\text{prd }1}$和${\mathcal{B}}_{\text{prd }2}$的中央点都重叠。因此，GIoU（${\mathcal{B}}_{\text{gt }}$，${\mathcal{B}}_{\text{prd }1}$）=GIoU（${\mathcal{B}}_{\text{gt }}$，${\mathcal{B}}_{\text{prd }2}$），DIoU（${\mathcal{B}}_{gt}$，${\mathcal{B}}_{\text{prd }1}$）=DIoU（${\mathcal{B}}_{gt}$，${\mathcal{B}}_{\text{prd }2}$），CIoU（${\mathcal{B}}_{gt}$，${\mathcal{B}}_{\text{prd }1}$）=CIoU（${\mathcal{B}}_{\text{gt }}$，${\mathcal{B}}_{\text{prd }2}$），EIoU（${\mathcal{B}}_{\text{gt }}$，${\mathcal{B}}_{\text{prd }1}$）=EIoU（${\mathcal{B}}_{\text{gt }}$，${\mathcal{B}}_{\text{prd }2}$），但是MPDIoU（${\mathcal{B}}_{\text{gt }}$，${\mathcal{B}}_{\text{prd }1}$）＞MPDIoU（${\mathcal{B}}_{gt}$，${\mathcal{B}}_{prd2}$）。


考虑到groundtruth边界框${\mathcal{B}}_{gt}$是一个面积大于零的矩形，即$A^{gt}>0$。算法2（1）和算法2（6）中的条件分别确保预测面积$A^{prd}$和交集面积$\mathcal{I}$是非负值，即$A^{\text{prd }}\ge 0$且$\mathcal{I}\ge 0$，对于任何预测边界框${\mathcal{B}}_{\text{prd }}=\left(x_1^{\text{prd }},y_1^{\text{prd }},x_2^{prd},y_2^{\text{prd }}\right)\in {\mathbb{R}}^4$。因此，对于任何预测边界框${\mathcal{B}}_{prd}=\left(x_1^{prd},y_1^{prd},x_2^{prd},y_2^{prd}\right)\in {\mathbb{R}}^4$，并集面积$\mathcal{U}$总是大于交集面积$\mathcal{I}$，即$\mathcal{U}\ge \mathcal{I}$。因此，${\mathcal{L}}_{MPDIoU}$总是有界的，即$0\le {\mathcal{L}}_{MPDIoU}<3$，对于任何预测边界框${\mathcal{B}}_{\text{prd }}\in {\mathbb{R}}^4$。

当$IoU=0$时，MPDIoU的行为：对于MPDIoU损失，我们有${\mathcal{L}}_{MPDIoU}=1-MPDIoU=1+\frac{d_1^2}{d^2}+\frac{d_2^2}{d^2}-IoU$。在${\mathcal{B}}_{gt}$和${\mathcal{B}}_{\text{prd}}$不重叠的情况下，这意味着IoU=0，MPDIoU损失可以简化为${\mathcal{L}}_{MPDIoU}=1-MPDIoU=1+\frac{d_1^2}{d^2}+\frac{d_2^2}{d^2}$。在这种情况下，通过最小化${\mathcal{L}}_{MPDIoU}$，我们实际上最小化了$\frac{d_1^2}{d^2}+\frac{d_2^2}{d^2}$。该项是一个介于0和1之间的归一化度量，即0≤$\frac{d_1^2}{d^2}+\frac{d_2^2}{d^2}<2$。

4、实验结果

我们通过将新的边界框回归损失${\mathcal{L}}_{MPDIoU}$纳入最流行的2D对象检测器和实例分割模型（如YOLO v7[6]和YOLACT[26]）来评估它。为此，我们将它们的默认回归损失替换为${\mathcal{L}}_{MPDIoU}$，即替换YOLACT[26]中的${\ell }_1-$smooth和YOLO v7[6]中的${\mathcal{L}}_{\text{CIoU }}$。我们还将基线损失与${\mathcal{L}}_{GIOU}$进行比较。

4.1、 实验设置

实验环境可以总结如下：内存为32 GB，操作系统为Windows 11，CPU为Intel i9-12900k，显卡为NVIDIA Geforce RTX 3090，内存为24GB。为了进行公平比较，所有实验都使用PyTorch[54]实现。

4.2、数据集

我们训练所有对象检测和实例分割基线，并在两个标准基准上报告所有结果，即PASCAL VOC [10]和Microsoft Common Objects in Context (MS COCO 2017) [11]挑战。它们的训练协议和评估细节将在各自的章节中解释。

PASCAL VOC 2007&2012：Pascal Visual Object Classes (VOC) [10]基准是最广泛使用的用于分类、对象检测和语义分割的数据集之一，包含约9963张图像。训练数据集和测试数据集各占50％，其中来自20个预定义类别的对象用水平边界框标注。由于实例分割图像的尺寸较小，导致性能较弱，我们只提供使用MS COCO 2017训练的实例分割结果。

MS COCO：MS COCO [11]是一个广泛用于图像captioning、对象检测和实例分割的基准，包含超过20万张图像，包括训练、验证和测试数据集，以及超过50万个标注的对象实例，来自80个类别。

IIIT5k：IIIT5k [12]是流行的场景文本检测基准之一，具有字符级别的注释，包含从互联网上收集的5000张裁剪的单词图像。字符类别包括英文字母和数字。有2000张图像用于训练，3000张图像用于测试。

MTHv2：MTHv2 [13]是流行的OCR基准之一，具有字符级别的注释。字符类别包括简化和传统的汉字。它包含超过3000张中文历史文献的图像和超过1百万个汉字。

4.3、 评估协议

在本文中，我们使用与MS COCO 2018挑战[11]相同的性能指标来报告所有结果，包括针对不同类别标签的mAP，以确定真正例和假正例的特定值IoU阈值。我们的实验中使用的对象检测的主要性能指标以精度（precision）和[email protected]:0.95的形式显示。我们在表中报告IoU阈值为0.75的AP75值。对于实例分割，我们的实验中使用的主要性能指标以AP和AR的形式显示，即在不同IoU阈值上平均mAP和mAR，即IoU={0.5,0.55,…0.95}。

所有对象检测和实例分割基线也使用MS COCO 2017和PASCAL VOC 2007&2012的测试集进行了评估。结果将在下一节中展示。

4.4、 目标检测的实验结果

训练协议。我们使用[6]发布的原始Darknet实现的YOLO v7。对于基线结果（使用GIoU损失进行训练），我们在所有实验中选择了DarkNet-608作为主干，并使用报告的默认参数和每个基准的迭代次数完全按照其训练协议进行训练。要使用GIoU、DIoU、CIoU、EIoU和MPDIoU损失训练YOLO v7，我们只需将边界框回归IoU损失替换为${\mathcal{L}}_{\text{GIoU}}$、${\mathcal{L}}_{\text{DIoU}}$、${\mathcal{L}}_{CIoU}$、${\mathcal{L}}_{\text{EIoU}}$和${\mathcal{L}}_{\text{MPDIoU}}$损失，这些损失在2中进行了说明。

根据原始代码的训练协议，我们将YOLOv7[6]使用每个损失在数据集的训练集和验证集上训练了最多150个epoch。我们将早期停止机制的容忍设置为5，以减少训练时间并保存性能最佳的模型。使用每种损失的最佳检查点，在PASCAL VOC 2007&2012的测试集上评估了它们的性能。结果已在表1中报告。

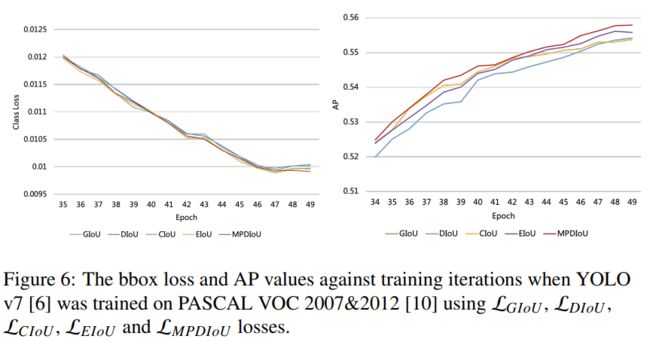
4.5、 字符级场景文本识别的实验结果

训练协议。我们使用与对象检测实验相似的训练协议。按照原始代码的训练协议，我们在该数据集的训练集和验证集上使用每个损失对YOLOv7[6]进行了最多30个epoch的训练。使用每个损失的最佳检查点评估了它们在IIIT5K[12]和MTHv2[55]测试集上的性能。结果已在表2和表3中报告。

正如我们所看到的，Tab.2和Tab.3中的结果显示，使用${\mathcal{L}}_{MPDIoU}$作为回归损失训练YOLO v7可以显着提高其性能，与现有的包括${\mathcal{L}}_{\text{GIoU}}，{\mathcal{L}}_{\text{DIoU}}，{\mathcal{L}}_{\text{CIoU}}，{\mathcal{L}}_{\text{EIoU}}$的回归损失相比。我们提出的${\mathcal{L}}_{MPDIOU}$在字符级场景文本检测方面表现出优异的性能。

4.6、 实例分割的实验结果

训练协议。我们使用了加州大学发布的最新PyTorch实现的YOLACT[26]。对于基线结果（使用${\mathcal{L}}_{GIoU}$训练），我们在所有实验中选择了ResNet-50作为YOLACT的主干网络架构，并使用报告的默认参数和每个基准的迭代次数按照其训练协议进行训练。要使用GIoU、DIoU、CIoU、EIoU和MPDIoU损失训练YOLACT，我们用${\mathcal{L}}_{\text{GIoU}}$、${\mathcal{L}}_{\text{DIoU}}$、${\mathcal{L}}_{CIOU}$、${\mathcal{L}}_{\text{EIoU}}$和${\mathcal{L}}_{MPDIOU}$损失替换了它们在最终边界框细化阶段的${\ell }_1-smooth$损失，这些损失在2中进行了说明。与YOLO v7实验类似，我们将原始的边界框回归损失替换为我们提出的${\mathcal{L}}_{\text{MPDIoU}}$。

如图8©所示，将${\mathcal{L}}_{GIoU}$、${\mathcal{L}}_{DIoU}$、${\mathcal{L}}_{CIoU}$和${\mathcal{L}}_{EIoU}$作为回归损失可以稍微提高YOLACT在MS COCO 2017上的性能。然而，与使用${\mathcal{L}}_{MPDIoU}$训练的情况相比，其改进是显着的，我们可视化了不同值的mask AP与不同值的IoU阈值之间的关系，即0.5≤IoU≤0.95。

与上述实验类似，使用${\mathcal{L}}_{MPDIoU}$作为回归损失可以提高检测准确率，超过现有的损失函数。如表4所示，我们提出的${\mathcal{L}}_{\text{MPDIoU}}$在大多数指标上比现有损失函数表现更好。但是，不同损失之间的改进幅度小于之前的实验。这可能是由于以下几个因素。首先，YOLACT [26]上的检测锚框比YOLO v7 [6]更密集，导致${\mathcal{L}}_{\text{MPDIoU}}$相对于${\mathcal{L}}_{IoU}$具有优势的情况（例如不重叠的边界框）更少。其次，过去的几年中，用于边界框回归的现有损失函数已经得到了改进，这意味着准确率的提高非常有限，但是效率仍有很大的提升空间。

我们还比较了YOLACT使用不同回归损失函数时训练期间的bbox loss和AP值的变化趋势。如图8(a)、(b)所示，使用${\mathcal{L}}_{MPDIOU}$进行训练比大多数现有损失函数（即${\mathcal{L}}_{GIoU}$、${\mathcal{L}}_{DIOU}$）表现更好，达到了更高的准确率和更快的收敛速度。尽管bbox loss和AP值显示出很大的波动，但我们的提出的${\mathcal{L}}_{MPDIoU}$在训练结束时表现更好。

为了更好地展示不同损失函数对于实例分割边界框回归的性能，我们提供了如图5和9所示的一些可视化结果。我们可以看到，除了${\mathcal{L}}_{\text{GIoU}}$、${\mathcal{L}}_{\text{DIoU}}$、${\mathcal{L}}_{\text{CIoU}}$和${\mathcal{L}}_{EIoU}$外，我们使用${\mathcal{L}}_{MPDIoU}$提供了更少冗余和更高精度的实例分割结果。

5、 结论

在本文中，我们介绍了一种新的度量方法，即基于最小点距离的MPDIoU，用于比较任意两个任意边界框。我们证明了这种新度量方法具有现有IoU基度量所具有的所有吸引力，同时简化了其计算。在所有依赖于IoU度量的2D/3D视觉任务中，它都将是更好的选择。

我们还提出了一个名为${\mathcal{L}}_{MPDIOU}$的损失函数，用于边界框回归。我们使用通用性能度量方法和我们提出的MPDIoU，将其应用于state-of-the-art对象检测和实例分割算法，从而改进了在PASCAL VOC、MS COCO、MTHv2和IIIT5K等流行基准测试上的性能。由于对于一个度量的最优损失是该度量本身，因此我们的MPDIoU损失可以作为所有需要2D边界框回归的应用中的最优边界框回归损失。

对于未来工作，我们希望在基于对象检测和实例分割的一些下游任务上进一步实验，包括场景文本检测、人员重识别等。通过上述实验，我们可以进一步验证我们提出的损失函数的泛化能力。