【论文阅读笔记】Reliability-Aware Joint Optimization for Cooperative Vehicular Communication and Computing
文章目录
- 论文基本信息
- 摘要
- 1.引言
-
- 总结
- 贡献
- 2.相关工作
- 3.系统模型(V2V通信和计算卸载)⭐
-
- A.System Analysis 系统分析
- B.Communication Model 通信模型
- C.Computation Model 计算模型
- D.Virtual Queu Model 虚拟队列模型
- 4.协同计算的优化模型⭐
-
- A. Optimization Algorithm for Joint Reliability 联合可靠性的优化算法
- B. Complexity Analysis 复杂度分析
- 5.仿真结果
- 6.总结
- 知识补充
-
- 涉及到的一些术语解释
论文基本信息
《Reliability-Aware Joint Optimization for Cooperative Vehicular Communication and Computing》
《面向可靠性的合作车辆通信和计算的联合优化》
论文链接:https://ieeexplore.ieee.org/document/9293144/
期刊:IEEE TRANSACTIONS ON INTELLIGENT TRANSPORTATION SYSTEMS, VOL. 22, NO. 8, AUGUST 2021
作者:有 Fellow,
本文到底在做什么事情?——优化车联网中各车辆之间的计算工作量分配,使协同通信与计算的耦合可靠性最大化。
摘要
利用概率理论建立了车对车(V2V)通信可靠性的随机模型。
并将计算信度定义为一种新的计算卸载度量指标,并建立了车辆计算性能评价模型。
此外,我们提出了一个结合队列长度和车辆隐私熵的虚拟队列模型来优化划分。(句子中的“queue”指的是一个虚拟队列,用于管理车联网中等待计算资源处理的任务。本文提出的虚拟队列模型结合队列长度和车辆隐私熵来优化网络中车辆之间的任务划分。)
最后,考虑到车辆应用的处理数据量和截止时间,建立了以最大化耦合可靠性为目标的车辆计算最优划分模型,并提出了基于动态规划方法的面向耦合的车辆协作可靠性计算方法。(这里的“耦合可靠性”是指一组车辆在给定的期限内成功完成协同通信和计算任务的概率。)(本文提出了一种面向耦合的可靠性计算方法,该方法同时考虑了车对车通信的可靠性和部分卸载的可靠性,以优化网络中车辆间的任务划分,使耦合可靠性最大化。)(V2V通信的可靠性是用概率论来建立的,计算卸载的可靠性定义为车辆在给定期限内成功计算一定数量数据的概率。|这是作者定义的一种新的度量指标)
1.引言
总结
本文的引言部分概述了车载通信和计算系统的现状,并强调了通过协作通信和计算来提高系统性能的必要性。
作者提出了一种新的计算卸载度量,称为计算可靠性,它被定义为车辆在给定期限内成功计算一定数量数据的概率。
他们还引入了车辆计算的虚拟队列模型和最优分区模型,以最大限度地提高耦合可靠性,即一组车辆在给定期限内成功完成协作通信和计算任务的概率。
最后,仿真结果表明,与传统方法相比,该方法在提高耦合可靠性和完成率方面是有效的。
贡献
- 提出了V2V通信动力学的随机建模。建立了一个表征V2V链路的可靠性(即在最后期限内通过V2V连接传输数据的成功概率)的分析模型。
- 提出了一个评估模型来描述计算可靠性,定义为车辆在期限内成功计算一定数量数据的概率。
- 提出了一个虚拟队列模型来优化分区。最后,我们结合V2V通信的可靠性建模和部分卸载,提出了基于动态规划的约束优化问题。其目标是通过优化V2V协作者之间的数据工作负载分区,最大限度地提高车辆协作通信和计算的耦合可靠性。
2.相关工作
介绍了移动边缘计算。
现有的车辆通信和计算的文献关注——计算任务卸载、资源分配、能耗优化、时间约束。
最近提出了有效的联合任务卸载和资源分配方案,包括提高卸载效用[22]、降低能源消耗和任务完成时间[23]、[24]、减少系统计算开销[25]在内的联合任务卸载和资源分配方案。(它们怎么怎么样,干了什么,)
(作者提出:局部计算和卸载联合计算下的可靠性度量尚未被研究。此外,还缺乏以可靠性为约束的联合计算方法。)
最后提了一嘴,最近还有一些隐私相关的研究。
3.系统模型(V2V通信和计算卸载)⭐
A.System Analysis 系统分析
构建了一个包含多个移动边缘计算(MEC)服务器和多个请求车辆的网络场景。这些服务器被部署在无线和计算资源有限的移动车辆上。这些车辆也被称为服务车辆。
请求车辆的计算任务可以由其自己的资源在本地执行。此外,在服务车辆通信范围内的请求车辆可以将任务卸载给服务车辆。模型中没有核心调度程序,任务卸载调度由请求的车辆完成。根据现有的文献,如[35],[36],我们可以使用以下两个关键参数来描述这个移动应用程序的轮廓:
- 输入数据大小 D D D:是作为应用程序输入的数据比特的总数。这些 D − b i t D-bit D−bit数据可以被分区和卸载到服务车辆,服务车辆是远程执行的云边缘。
- 应用完成截止日期 T T T:表示移动应用完成之前的最大连续时隙数。此外,我们使用 t ( 从 T 到 1 ) t(从T到1) t(从T到1)(这里T是比1大的,也就是说,t从T开始,一直到1,代表进程中每一个连续的时隙。)来表示时隙,这些 D − b i t D-bit D−bit数据也可以被分割成一系列较小的片段 s ∈ [ 0 , D ] s∈[0, D] s∈[0,D],其中 s t s_t st表示应该在 t i t_i ti时隙传输到服务节点的数据位数。
我们假设每个被卸载的任务只被分配给一个服务器。此外,每个车辆节点都有一个队列缓冲区来存储任务的到达情况。表示时间段 t t t中的请求车辆(源节点 s s s)和服务车辆(目标节点 d d d)的任务队列长度分别为 Q s ( t ) Q_s (t) Qs(t)和 Q d ( t ) Q_d (t) Qd(t)。
(注意!:作者假设“每个被卸载的任务只被分配给一个服务器,”这个假设简化了任务卸载过程,并允许更容易地对系统进行建模和分析。)
总结——
定义了系统——一个请求车辆会将被卸载的任务分配给一个服务车辆。
过程中关注数据大小D和截止时间T。以及请求车辆和服务车辆的任务队列长度Qs(t)和Qd(t)
B.Communication Model 通信模型
假设每对V2V对通过瑞利衰落信道(Rayleigh fading channels)进行通信。定义了一种基于协同传输的通信模型。请求车辆(源节点 s s s)和服务车辆(目的地节点 d d d)之间的无线链路可以用以下模型表示

其中, S D SD SD为请求车辆与服务车辆之间的距离。
由于 k k k是路径损耗系数, S D k / 2 SD^{k/2} SDk/2根据两车之间的距离计算信道增益。 h s , d h_{s,d} hs,d描述了信道的衰落特性。(由于干扰和障碍物等因素,信道的衰落特性可以随时间和空间变化)。 c s , d c_{s,d} cs,d是一个连接变量。当请求车辆与服务节点之间建立连接时, c s , d = 1 c_{s,d}=1 cs,d=1,否则为 0 0 0。(该连接变量用于模拟两辆车之间无线链路的可靠性。)

考虑图1中的三节点场景,源节点s希望在中继节点r的帮助下与目标节点d进行通信。假设当接收到的信噪比(SNR)超过一个阈值时,中继节点能够进行完美的解码,则该合作链路的互信息可以显示为

(笔者:互信息是信息论中的一个概念,用来衡量两个随机变量之间共享的信息量。在本文中,源节点s、目的节点d和中继节点r之间的合作链路互信息是衡量这些节点之间通过无线链路可以传输的信息量的度量。互信息根据无线链路的信噪比和中继节点的解码阈值计算。互信息是评价车载系统协同通信和计算性能的一个重要指标,它提供了节点之间可以可靠传输的信息量的度量。)
信噪比 S N R SNR SNR 和 S N R ′ SNR' SNR′ 分别是路径 s − > d s->d s−>d 和 r − > d r->d r−>d 的信噪比。
q ( S N R ) = 2 2 R − 1 S N R q(SNR)=\frac{2^{2R}-1}{SNR} q(SNR)=SNR22R−1,其中R是被服务质量Qos定义的以bits/s/Hz为单位的数据速率。
由于假设 h s , d h_{s,d} hs,d是一个均值和单位方差为 0 0 0的复高斯变量,因此 ∣ g s , d ∣ 2 = ∣ h s , d S D k / 2 ∣ 2 |g_{s,d}|^2=|\frac{h_{s,d}}{SD^{k/2}}|^2 ∣gs,d∣2=∣SDk/2hs,d∣2是一个参数为 S D k / 2 SD^{k/2} SDk/2的指数分布变量。
从参考文献[4]中得出,源节点s和目标节点d之间的协同传输的中断概率为:
应用程序需要确定在每个时间段 t t t 中将分别由本地车辆和服务车辆执行多少数据,目的是最小化移动设备上的总不可靠性。具体来说,在给定阈值下的分布策略由以下决策规则决定

其中, λ t λ_t λt为时隙 t t t中的比例系数。
(笔者:时隙t中的比例系数λt表示在该时隙中,剩余数据从请求车辆卸载到服务车辆的比例。它用于平衡请求车辆和服务车辆之间的负载,并根据时间段开始时队列的长度Qs(t)和Qd(t)确定。比例系数是拟议系统中的一个重要参数,因为它决定了数据从请求车辆卸载到服务车辆的速率,从而影响系统的整体性能和可靠性。通过优化比例系数,该系统可以实现更好的负载均衡,提高车载系统协同通信和计算的可靠性。???TODO)
因此,本地执行 s t s s_t^s sts 和服务车辆执行 s t d s_t^d std的数据大小分别表示为 s t s = λ t s t s_t^s = λ_ts_t sts=λtst和 s t d = ( 1 − λ t ) s t s_t^d =(1−λ_t)s_t std=(1−λt)st。(笔者:下文中的公式(15)(16)涉及了比例系数 λ λ λ的求法。它决定了数据从请求车辆卸载到服务车辆的速率,从而影响系统的整体性能和可靠性。)。
于是可以把公式(3)(源节点s和目标节点d之间的协同传输的中断概率)重写为——

总结——
通过Rayleigh fading channels定义了源节点s和目标节点d之间的无线链路模型。
定义了三节点 s,r,d 场景(源节点s希望在中继节点r的帮助下与目标节点d进行通信)中合作链路的互信息量。
从参考文献[4]中引入了协同传输的中断概率 P s , d ( R ) P_{s,d}(R) Ps,d(R),之后引入比例系数 λ λ λ 重写了中断概率为 P s , d ( s t ) P_{s,d}(s_t) Ps,d(st)。
C.Computation Model 计算模型
图1的顶部显示了车辆节点的架构,其中包括一个处理器,数据存储组件,如存储器和缓存,一个单服务器的存储到达任务的第一输入第一输出(FIFO)队列,以及一个无线接口。
我们用 B B B表示带宽, W W W表示CPU周期数。
设 W W W表示一个应用程序所需的CPU周期数。对于给定的输入数据大小为 L L L,它可以推导出为 W = L X W=LX W=LX。
![]()
假设X的概率分布函数PDF为 P X ( x ) P_X(x) PX(x),其累积分布函数CDF为 F X ( x ) F_X(x) FX(x),互补累积分布函数CCDF F X c ( x ) = 1 − F X ( x ) F_X^c(x)=1-F_X(x) FXc(x)=1−FX(x)。因此工作负载 W W W的CCDF互补累积分布函数为 F W c ( w ) = F X c ( w / L ) F_W^c(w)=F_X^c(w/L) FWc(w)=FXc(w/L)。
(笔者:X的含义是?TODO)
根据参考文献[35],每比特的CPU周期数可以用伽玛分布来建模。伽马分布的PDF(概率分布函数)为——

(笔者:“每比特的CPU周期数”是指处理一位数据所需的CPU周期数的平均值。)
伽马分布的CDF(累积分布函数)为——
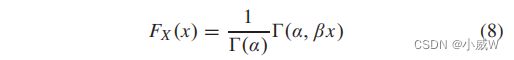
而伽马分布有两个推论:
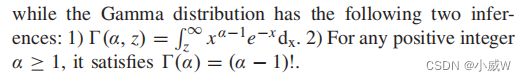
笔者使用软截止时间来表征概率性能——即统计CPU调度模型。
假设通过分配 W p W_p Wp 的 CPU周期来以概率 p p p 满足截止时间。这里参数 p p p 是应用程序完成的概率(ACP)。
换句话说,一个这样概率 p p p 的应用程序如果需要不超过 W p Wp Wp,那么就需要满足 ( F W c ) − 1 ( p ) = P r [ W ≤ W p ] ≥ p (F_W^c)^{-1}(p)=Pr[W\le W_p]\ge p (FWc)−1(p)=Pr[W≤Wp]≥p。(笔者:互补累积分布函数的反函数可以用来生成服从该随机分布的随机变量。e.g.一个实际例子是,假设我们有一个随机变量X,它代表着某个人的年龄。那么,互补累积分布函数的反函数可以告诉我们,有多少人的年龄大于等于某个值。)
在本工作中,如果请求车辆分配的 W p W_p Wp 不足以支持应用程序完成计算任务,则成功的概率计算如下:
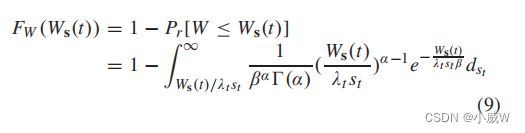
(笔者:这个公式是不是错了?累积分布函数为什么会有1- 呢?TODO)
总结:
最后推出了——
1.不超过Wp完成的条件
2.不满足条件时的成功率
D.Virtual Queu Model 虚拟队列模型
根据利特尔定律,平均排队时延与平均队列长度[37]成正比。此外,队列长度/队列延迟 过长 最终会破坏任务计算的可靠性。
在前面 A——C 系统模型的基础上,作者提出了虚拟队列的概念。(如图2)

初始时隙 t = T + 1 t = T + 1 t=T+1。(笔者:虽然优化过程从最后一个时隙T开始,但实际上它是实践中的最后一个时隙,因为它是必须传输剩余数据位以满足端到端延迟约束的时隙。)
在本文中,端到端延迟约束间接地由服务车辆的虚拟队列长度来表示。(笔者:端到端延迟约束是指在请求车辆提交任务的时间和服务车辆完成任务的时间之间允许的最大延迟。在该系统中,采用虚拟队列模型间接表示端到端延迟约束。具体而言,将服务车的虚拟队列长度作为任务所经历的延迟的度量,并在端到端延迟约束下制定了最小化虚拟队列长度的优化问题。
因此,服务车的虚拟队列长度可以间接表示系统中的端到端延迟约束。通过最小化虚拟队列长度,既能满足端到端延迟约束,又能保证任务计算的可靠性。)
对于当前的决策时间 t t t,使用 A ( Q s ′ ( t ) , Q d ( t ) ) A(Q_s'(t),Q_d(t)) A(Qs′(t),Qd(t)) 存储网络的虚拟队列状态。
其中请求车辆 s 的真实队列长度和服务车辆 d 的真实队列长度分别定义为 Q s ( t ) Q_s(t) Qs(t)和 Q d ( t ) Q_d(t) Qd(t)。
假设系统在 t 时隙开始处的任务数与前一个时隙相同,即 Q ( t ) = s t + 1 Q (t) = s_{t+1} Q(t)=st+1。然后由 s t + 1 s_{t+1} st+1和先验参数 λ t + 1 λ_{t+1} λt+1(根据公式(4)中提供的决策规则)确定先验虚拟队列 Q s ′ ( t ) Q_s'(t) Qs′(t),可以推导为:
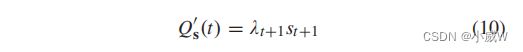
相似地,在时隙 t 开始处,d 的鲜艳虚拟队列长度为:


WdH表示大的CPU周期,WdL表示小的CPU周期。Xd是应用程序为服务车辆计算每秒比特数据所需的CPU周期数。
(笔者:如果任务需要大量的CPU周期来处理,则为其分配一个WdH值,而如果任务需要较少的CPU周期,则为其分配一个WdL值。然后根据WdH和WdL的值计算Xd的值,Xd表示应用程序为服务车辆计算每秒每比特的数据所需的CPU周期数。)
该系统没有提供一个隐私保护机制,而是试图在量化车辆的隐私感知方面取得进展。为此,我们使用隐私熵来进一步定义隐私暴露率。(笔者:本文将隐私熵定义为隐私敏感信息的概率分布函数(PDF)的香农熵。隐私熵的概念很重要,因为它允许论文量化隐私敏感信息分布中的不确定性或随机性的数量,并为车载系统中的隐私保护建立一个新的度量。)

其中, p ^ i \hat{p}_i p^i 表示为在通信过程中每个消息与服务车辆相关联的概率,并随着时间的变化而更新。假设攻击者的目的是确定任务接收者对请求的意愿和行为,那么在系统中的每个时隙 t 中,服务车辆以一定的概率被猜测为真正的服务提供者。
在没有任何最优调度的情况下,服务车辆认为服务事件在每个时隙中发生的概率相等,即车辆 d 被确定为每个时隙中的服务提供者,在这种情况下其最大熵
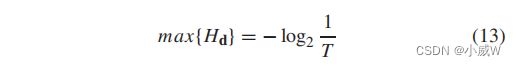
(TODO 这个公式怎么推出来的还没确定—— p = 1/T 时就是了。)
作者提出 P r i d Pri_d Prid 来评价服务车辆 d 的隐私等级。它表示服务车辆对卸载事件的隐私[38]的主观感知。

因此, 1 − P r i d 1−Pri_\mathbf{d} 1−Prid表示由对服务车辆d的主观感知所决定的隐私暴露率。
Prid值的增加意味着卸载事件受到保护,即隐私泄漏率降低,被攻击的概率降低,反之亦然。
在该模型中,当1−Prid小于给定的阈值φ时,取时隙i中的Wd (i)为WdH,否则取Wd (i)为WdL。(见公式(11)下的解释)
假设初始阈值 λ T λ_T λT 服从标准的均匀分布(即 λ T ∼ U ( 0 , 1 ) λ_T∼U(0,1) λT∼U(0,1))。用 l t l_t lt 表示在时间隙 t t t 开始时需要卸载的数据比特的数量。根据前面的陈述,我们有 Q s ′ ( T ) = λ T l T Q_s' (T) = λ_T l_T Qs′(T)=λTlT 和 Q d ′ ( T ) = ( 1 − λ T ) l T Q_d' (T) =(1−λ_T)l_T Qd′(T)=(1−λT)lT。
为了实现整个系统的负载平衡,时隙 t 中的比例系数 λ t λ_t λt 由如下公式确定——

总结:
优化时的初始时隙是 T + 1
先定义了请求和服务车辆的真实队列长度
然后推导了虚拟队列长度由 λ λ λ 和 s s s 确定。 (s表示数据大小)
服务车辆的虚拟队列长度公式中包含额外一项,由隐私相关指标确定。
最后给出了 λ t λ_t λt 的求法。
4.协同计算的优化模型⭐
A. Optimization Algorithm for Joint Reliability 联合可靠性的优化算法
考虑 T 个时隙中 D bits 应用数据的传输调度优化。
提出了基于(5)和(9)的V2V传输调度优化模型。目标是最大限度地提高计算卸载的估计成功概率。

简单表示成如下:

B. Complexity Analysis 复杂度分析
5.仿真结果
6.总结
知识补充
涉及到的一些术语解释
Computational partitioning:计算划分是实现边缘计算[9]的核心功能之一。它允许单个车辆终端避免处理所有的计算负载,而是将整个应用程序划分为几个计算子任务,然后根据网络连接的状态、计算负载和应用程序处理需求,将它们分配给对等车辆或RSU进行处理。
Computational offloading:计算卸载也是实现边缘计算的一个重要功能。目前关于计算卸载的研究主要是为了优化系统能耗或联合优化能量和延迟。该通信模型通常被认为是一个稳定的蜂窝通信网络或WLAN网络。实际上,在车辆计算方案中需要考虑车辆网络传输的固有特性。


