最小生成树的变形（次小生成树hdu4081）

hdu4081

Qin Shi Huang's National Road System

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 3342    Accepted Submission(s): 1171

Problem Description

During the Warring States Period of ancient China(476 BC to 221 BC), there were seven kingdoms in China ---- they were Qi, Chu, Yan, Han, Zhao, Wei and Qin. Ying Zheng was the king of the kingdom Qin. Through 9 years of wars, he finally conquered all six other kingdoms and became the first emperor of a unified China in 221 BC. That was Qin dynasty ---- the first imperial dynasty of China(not to be confused with the Qing Dynasty, the last dynasty of China). So Ying Zheng named himself "Qin Shi Huang" because "Shi Huang" means "the first emperor" in Chinese.

Qin Shi Huang undertook gigantic projects, including the first version of the Great Wall of China, the now famous city-sized mausoleum guarded by a life-sized Terracotta Army, and a massive national road system. There is a story about the road system:
There were n cities in China and Qin Shi Huang wanted them all be connected by n-1 roads, in order that he could go to every city from the capital city Xianyang.
Although Qin Shi Huang was a tyrant, he wanted the total length of all roads to be minimum,so that the road system may not cost too many people's life. A daoshi (some kind of monk) named Xu Fu told Qin Shi Huang that he could build a road by magic and that magic road would cost no money and no labor. But Xu Fu could only build ONE magic road for Qin Shi Huang. So Qin Shi Huang had to decide where to build the magic road. Qin Shi Huang wanted the total length of all none magic roads to be as small as possible, but Xu Fu wanted the magic road to benefit as many people as possible ---- So Qin Shi Huang decided that the value of A/B (the ratio of A to B) must be the maximum,which A is the total population of the two cites connected by the magic road, and B is the total length of none magic roads.
Would you help Qin Shi Huang?
A city can be considered as a point, and a road can be considered as a line segment connecting two points.

 

Input

The first line contains an integer t meaning that there are t test cases(t <= 10).
For each test case:
The first line is an integer n meaning that there are n cities(2 < n <= 1000).
Then n lines follow. Each line contains three integers X, Y and P ( 0 <= X, Y <= 1000, 0 < P < 100000). (X, Y) is the coordinate of a city and P is the population of that city.
It is guaranteed that each city has a distinct location.

 

Output

For each test case, print a line indicating the above mentioned maximum ratio A/B. The result should be rounded to 2 digits after decimal point.

 

Sample Input

  
    

     
   2
4
1 1 20
1 2 30
200 2 80
200 1 100
3
1 1 20
1 2 30
2 2 40
  
    

 

Sample Output

  
    

     
   65.00
70.00
  
    

题意：在一个二维坐标系中给出n个城市的坐标以及该城市的人口，前期秦始皇为了节省钱，但又要联通所有的城市，就建立了一颗最小生成树，保证道路和最短，后来有一个法师拥有一种技能，他能造一条路仅且一条，这条路不需要花费任何费用，秦始皇想让除了这条路的其他路的总长度（B）最小，而那个法师想让这条魔幻路连接的两个城市的总人口（A）最多,所以怎样建立虚拟路才能使A/B的值最大；

分析:此题有两种方法：

（1）要保证A/B最大，这条魔幻路肯定取代的是最小生成树里的某条路，首先建立一颗最小生成树（sum）然后枚举删除最小生成树里的每一条边i，此时形成两个集合，然后分别从两个集合各找一个最大的人口数x和y，然后此时的A/B=（x+y）/（sum-e[i].w）;

比较大小即可；有可能最小生成树的会存在多个，那么为什么随便取一种就行呢？首先想想当最小生成树有多个的时候，他们的权值和一定是一样的，例如下图：

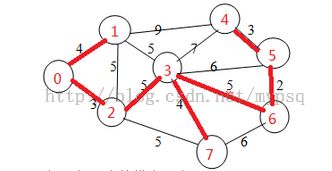首先介绍等效边：例如给出的最小生成树中，（1,3）和（2,3）就是等效边，就是说当联通两个集合的边的权值是一样的他们就是等效边，现在就好理解上面的疑问了，当删除（2,3）这条边时，形成两个集合，假如最小生成树有（1,3）这条边，删除后形成的两个集合是相同的，并不影响最终的结果；

（2）首先用dij求出任意一颗最小生成树，同时记录任意两个点在生成树路径中的最大边权，然后枚举每一条边，当边在生成树里面则比值是：

（p[i].z+p[j].z)/(ans-G[i][j])；否则是：(p[i].z+p[j].z)/(ans-maxd[i][j]);取最大值即可；

程序(1);

#include"stdio.h"
#include"string.h"
#include"iostream"
#include"map"
#include"string"
#include"queue"
#include"stdlib.h"
#include"math.h"
#define M 1009
#define eps 1e-8
#define inf 1000000000
#define mod 1000000000
#define INF 1000000000
using namespace std;
struct node
{
    int u,v,next;
    double w;
}e[M*M],edge[M*2];
int t,head[M],dis[M];
double maxdis;
double prep[M];
struct st
{
    double x,y,z;
}p[M];
int cmp(const void *a,const void *b)
{
    return (*(struct node*)a).w>(*(struct node*)b).w?1:-1;
}
void init()
{
    t=0;
    memset(head,-1,sizeof(head));
}
void add(int u,int v,double w)
{
    edge[t].u=u;
    edge[t].v=v;
    edge[t].w=w;
    edge[t].next=head[u];
    head[u]=t++;
}
int f[M];
int finde(int x)
{
    if(x!=f[x])
        f[x]=finde(f[x]);
    return f[x];
}
void dfs(int u,int f)//深搜查找最大值
{
    for(int i=head[u];i!=-1;i=edge[i].next)
    {
        int v=edge[i].v;
        if(f!=v)
        {
            dfs(v,u);
        }
    }
    if(maxdis<p[u].z)
    maxdis=p[u].z;
}
int mp[M];
int main()
{
    int T,i,j,n,m;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(i=1;i<=n;i++)
            scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].z);
        m=0;
        for(i=1;i<=n;i++)
        {
            for(j=i+1;j<=n;j++)
            {
                double L=sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y));
                e[m].u=i;
                e[m].v=j;
                e[m].w=L;
                m++;
            }
        }
        qsort(e,m,sizeof(e[0]),cmp);
        int kk=0;
        double sum=0;
        init();
        for(i=1;i<=n;i++)
            f[i]=i;
        for(i=0;i<m;i++)
        {
            int a=finde(e[i].u);
            int b=finde(e[i].v);
            if(a!=b)
            {
                mp[kk++]=i;
                sum+=e[i].w;
                f[a]=b;
                add(e[i].u,e[i].v,e[i].w);
                add(e[i].v,e[i].u,e[i].w);//建立最小生成树
            }
            if(kk==n-1)
                break;
        }
        double ans=0;
        for(i=0;i<kk;i++)//枚举最小生成树的边
        {
            double A=0,B;
            int u=e[mp[i]].u;
            int v=e[mp[i]].v;
            maxdis=0;
            dfs(v,u);
            A+=maxdis;
            maxdis=0;
            dfs(u,v);
            A+=maxdis;
            B=sum-e[mp[i]].w;
            ans=max(ans,A/B);
        }
        printf("%.2lf\n",ans);
    }
    return 0;
}

程序（2）：

#include"stdio.h"
#include"string.h"
#include"math.h"
#define inf 100000000
#define M 1111
int use[M],pre[M],vis[M][M];
double G[M][M],dis[M],maxd[M][M];
double max(double a,double b)
{
    return a>b?a:b;
}
double min(double a,double b)
{
    return a<b?a:b;
}
double dij(int u,int n)
{
    int i,j;
    double ans=0;
    memset(use,0,sizeof(use));
    memset(maxd,0,sizeof(maxd));//记录不在任意两点在在生成树的路径中的最长边
    memset(vis,0,sizeof(vis));//标记边是否在生成树里面
    for(i=1;i<=n;i++)
    {
        dis[i]=G[u][i];
        pre[i]=u;//记录父节点
    }
    dis[u]=0;
    use[u]=1;
    for(i=1;i<n;i++)
    {
        double mini=inf;
        int tep=-1;
        for(j=1;j<=n;j++)
        {
            if(!use[j]&&dis[j]<mini)
            {
                mini=dis[j];
                tep=j;
            }
        }
        if(tep==-1)break;
        use[tep]=1;
        vis[tep][pre[tep]]=vis[pre[tep]][tep]=1;
        ans+=mini;
        for(j=1;j<=n;j++)
        {
            if(!use[j]&&dis[j]>G[tep][j])
            {
                dis[j]=G[tep][j];
                pre[j]=tep;
            }
            if(j!=tep)
            maxd[tep][j]=maxd[j][tep]=max(mini,maxd[pre[tep]][j]);//更新
        }
    }
    return ans;
}
struct node
{
    double x,y,z;
}p[M];
double pow(double x)
{
    return x*x;
}
double Len(node a,node b)
{
    return sqrt(pow(a.x-b.x)+pow(a.y-b.y));
}
int main()
{
    int T,n,i,j;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(i=1;i<=n;i++)
            scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].z);
        for(i=1;i<=n;i++)
        {
            G[i][i]=0;
            for(j=i+1;j<=n;j++)
                G[i][j]=G[j][i]=Len(p[i],p[j]);
        }
        double ans=dij(1,n);
        //printf("%.2lf\n",ans);
        double maxi=0;
        for(i=1;i<=n;i++)
        {
            for(j=i+1;j<=n;j++)
            {
                if(vis[i][j])
                    maxi=max(maxi,(p[i].z+p[j].z)/(ans-G[i][j]));
                else
                    maxi=max(maxi,(p[i].z+p[j].z)/(ans-maxd[i][j]));
            }
        }
        printf("%.2lf\n",maxi);
    }
    return 0;
}