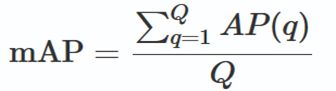目标检测评估指标mAP：从Precision,Recall,PR曲线到AP

1. TP, FP, FN, TN

True Positive

满足以下三个条件被看做是TP

        1. 置信度大于阈值（类别有阈值，IoU判断这个bouding box是否合适也有阈值）

        2. 预测类型与标签类型相匹配（类别预测对了）

        3. 预测的Bouding Box和Ground Truth的IoU大于阈值（框 打对了）。 当存在多个满足条件的预选框，则选择置信度最大的作为TP，其余的作为FP

False Positive

       1. 预测的 类别  和 真实的标签类型不匹配（分类错误）

        2. 预测的Bounding box和Ground Truth的IoU小于阈值（框  打的不是那么好， 定位错误）

False Negative

        分类争取，定位正确，但是被检测成了负样本

True Negative

        负样本被检测出的数量，太多了，绝大多数的框都是这个类型。后面计算precision和recall的时候用不到，所以这个东西也就不统计数量了。

2. Precision和Recall

Precision = TP/(TP+FP) = TP/(所有被我判定为正例的个数)

Recall = TP/(TP+FN) = TP/(所有世界是正例的个数)

3. PR曲线

Precision-Recall曲线是根据阈值 从0到1这个区间的变动，每个阈值下模型的precision和recall的值分别作为纵坐标和横坐标来连线绘制而成的。（每个阈值θ对应于一个（Precision,Recall）点，把这些点连起来就是PR曲线）

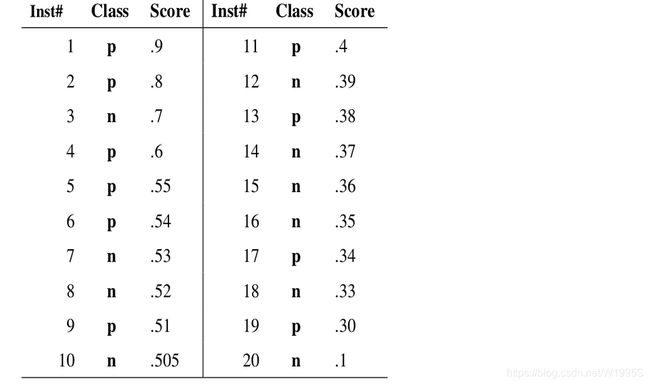
比如假设我们收集了20个sample的数据，他们的真实标签和置信度如下

 此时我们为了绘制PR曲线，计算出了PR曲线上下面这些点的坐标

阈值=0.9——TP=len([ #1, ]) = 1; FP=0; FN=len([#2, #4, #5, #6, #9, #11, #13, # 17, #19])=9——Precision=TP/(TP+FP)=1/(1+0)=1——Recall=TP/(TP+FN)=1/(1+9)= 0.1

阈值0.8——TP=len([#1,#2])=2; FP=0; FN=len([#4, #5, #6, #9, #11, #13, # 17, #19])=8——Precision=2/(2+0)=1; Recall=2/(2+8)=0.2

阈值0.7——TP=len([#1,#2])=2; FP=len([#3])=1, #_of_True=10 ——Precision=2/(2+1)=0.67；Recall=2/10=0.2

阈值0.6——TP=len([#1, #2，#4])=3;  FP=len([#3])=1, #_of_True=10——Precision=3/(3+1)=0.75; Recall = 3/10=0.3

阈值0.5——TP=len([#1, #2, #4， #5， #6， #9])=6; FP=len([#3, #7, #8, #10])=4,#_of_True=10——Precision=6/(6+4)=0.6; Recall = 6/10=0.6

阈值0.4——TP=len([#1, #2，#4， #5， #6， #9,  #11])=7; FP=len([#3, #7, #8, #10])=4, #_of_True=10——Precision=7/(7+4)=0.64; Recall = 7/10=0.7

阈值0.3——TP=len([#1, #2，#4， #5， #6， #9,  #11, #13, #17, #19])=10;FP=len([#3, #7, #8, #10, #12, #14, #15, #16, #18])=9; #_of_True=10; ——Precision=10/(10+9)=0.53; Recall = 10/10=1

用sklearn的下面这段代码就可以计算出答案

import numpy as np
from sklearn.metrics import precision_recall_curve

# 导入数据
y_true = np.array([1,1,0,1,1,1,0,0,1,0,1,0,1,0,0,0,1,0,1,0])
y_scores = np.array([0.9,0.8,0.7,0.6,0.55,0.54, 0.53,0.52,0.51,0.505, 0.4, 0.39,0.38, 0.37, 0.36, 0.35, 0.34, 0.33, 0.30, 0.1])

# 计算出每个阈值下，precision和recall的值
precision, recall, thresholds = precision_recall_curve(y_true, y_scores)

# 写上这两行，中间的列就不会被用省略号省略，都显示出来
pd.options.display.max_rows = None
pd.options.display.max_columns = None


#整理成横向的dataframe，方便大家查看
precision = pd.DataFrame(precision).T
recall = pd.DataFrame(recall).T
thresholds= pd.DataFrame(thresholds).T
#纵向拼接
results = pd.concat([thresholds, recall,precision], axis=0)
# 仅仅保留2位小数
results = round(results, 2)
#行名改一下
results.index = ["thresholds", "recall", "precision"]
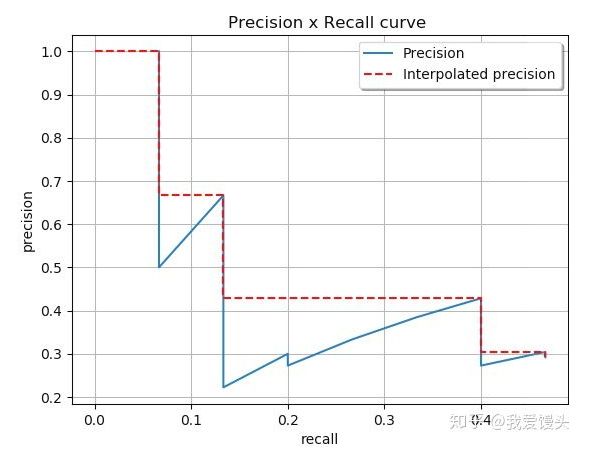
print(results)

绘制出来的precision-recall曲线是下面这样

import matplotlib.pyplot as plt
def plot_pr_curve(recall, precision):
    plt.plot(recall, precision, label='Precision-Recall curve')
    plt.xlabel('Recall')
    plt.ylabel('Precision')
    plt.title('PR Curve')
    plt.legend()
plot_pr_curve(recall, precision)

对于PR图中这种类似锯齿状的图形，我们一般采用平滑锯齿的操作。所谓平滑锯齿操作就是在Recall轴上，对于每个阈值θ计算出的Recall点，看看它的右侧（包含它自己）谁的Precision最大，然后这个区间都使用这个Precision值，在下图这个例子中，Recall=(0，0.4] 都使用 Precision=1, Recall=（0.4，0.8] 都使用 Precision=0.57， Recall=（0.8，1) 都使用 Precision=0.5

因此我们这个例子中的图形经过锯齿平滑化以后应该是下面这个样子

Precision和Recall之间的此消彼长的矛盾关系

        上图的右下角，recall高，说明所有所有的杀人犯中99%的都被抓住了，那就会造成一个结果，抓的人特别多。和这桩杀人案有一丁点关系的人都被逮捕了。这必然导致，所有被抓的人中，实际是罪犯的比例变得很低，也就是precision低。

        OK，如果你希望Police抓的人中，实际是罪犯的比例高一些，（也就是precision高一些）。那Police就不敢乱抓人了，没有十足的证据就不敢去逮人。那结果是啥？那就是大量隐藏额的很好的罪犯都被漏掉了，也就是说所有的罪犯中实际被抓住的比例降低了。也就是recall低了。这种情形对应的就是上图左上角的那个位置。

如何评估一个不同模型的好坏关系

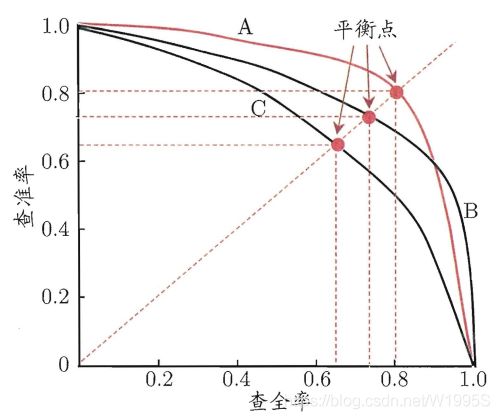
        既然一个模型的precision和recall是此消彼长的关系，不可能两个同时大，那怎么判断哪个模型更优呢？答案是，P-R曲线越往右上角凸起的曲线对应的模型越优秀。正如上图中红线A和黑线B都是比模型C要优秀的

        但是问题来了，模型A和模型B之间，孰优孰劣呢？那就引出了平衡点（"Balanced Error Point" (BEP)）这个概念。平衡点就是曲线上的Precision值=Recall值的那个点，也就是上图中那三个点，平衡点的坐标越大，模型越好。

        除了平衡点，也可以用F1 score来评估。F1 = 2 * P * R ／( P + R )。F1-score综合考虑了P值和R值，是精准率和召回率的调和平均值， 同样，F1值越大，我们可以认为该学习器的性能较好。

4. 从PR曲线到AP

AP的公式如下

AP这个指标的实际意义：

        AP是，在“”阈值不同“”引发的“Recall值不同”的情况下，各种Precision值的均值。AP summarizes a precision-recall curve as the weighted mean of precisions achieved at each threshold, with the increase in recall from the previous threshold used as the weight:

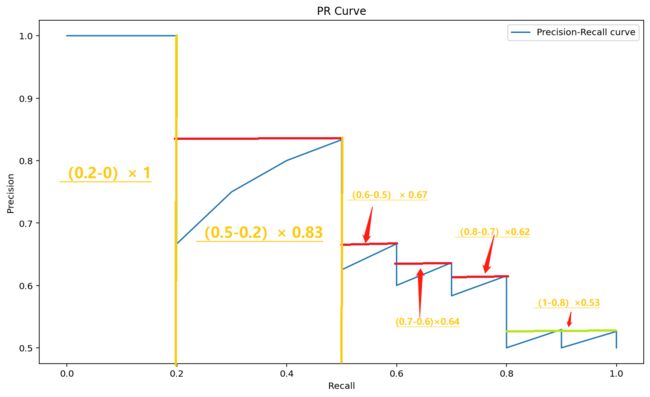
        AP值可以理解为PR曲线向下、向左到X轴和Y轴这片面积之和

        这个阈值到前一个阈值之间的差是长方形的宽，precision值是长方形的高。宽乘以高就是长方形柱子的面积。

        AP这就是P-R曲线的积分，也就是面积

用sklearn的公式这样算

from sklearn.metrics import average_precision_score
AP = average_precision_score(y_true, y_scores, average='macro', pos_label=1, sample_weight=None)
print(AP)

# 0.7357475805927818

AP=（0.2-0）× 1 + （0.5-0.2）× 0.83 + （0.6-0.5） × 0.67 + (0.7-0.6)×0.64 +（0.8-0.7）×0.62 +（1-0.8）×0.53=0.7480

和上面那个程序算出来来的有0.1的误差，但是大体区别不大就不去追究是哪个小地方算错了

5. 从AP到mAP

把各个类别（比如汽车、行人、巴士、自行车）的AP值取平均

6. 从mAP到 mAP50, mAP75, mAP95

mAP中也有IoU, mAP50这个也有IoU，二者之间是什么关联？

        mAP里面那个IoU是指的分类里面 判断类别上predicted label是True或False

        mAP50里面这个IoU指的是定位 里面 判断predicted bbox和ground truth bbox之间的IoU大于多少才能被算作  定位爱上的True或False

        mAP

目前还不懂的知识

        ROC曲线是什么？表示什么含义？怎么用？

        AUC曲线同样的问题

Reference

PR曲线与ROC曲线_roc曲线和pr曲线_THE@JOKER的博客-CSDN博客

为什么平均精准度（Average Precision，AP）就是PR曲线的线下面积？ - Mark Lue的回答 - 知乎 https://www.zhihu.com/question/422868156/answer/1523130474

sklearn.metrics.average_precision_score — scikit-learn 1.3.0 documentation

[CV] 目标检测中的map计算 - 知乎 

COCO - Common Objects in Context

https://www.cnblogs.com/ywheunji/p/13376090.html

准确率、召回率和mAP、AP50/75_map和ap50_dagongji10的博客-CSDN博客