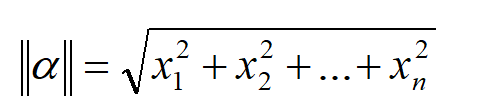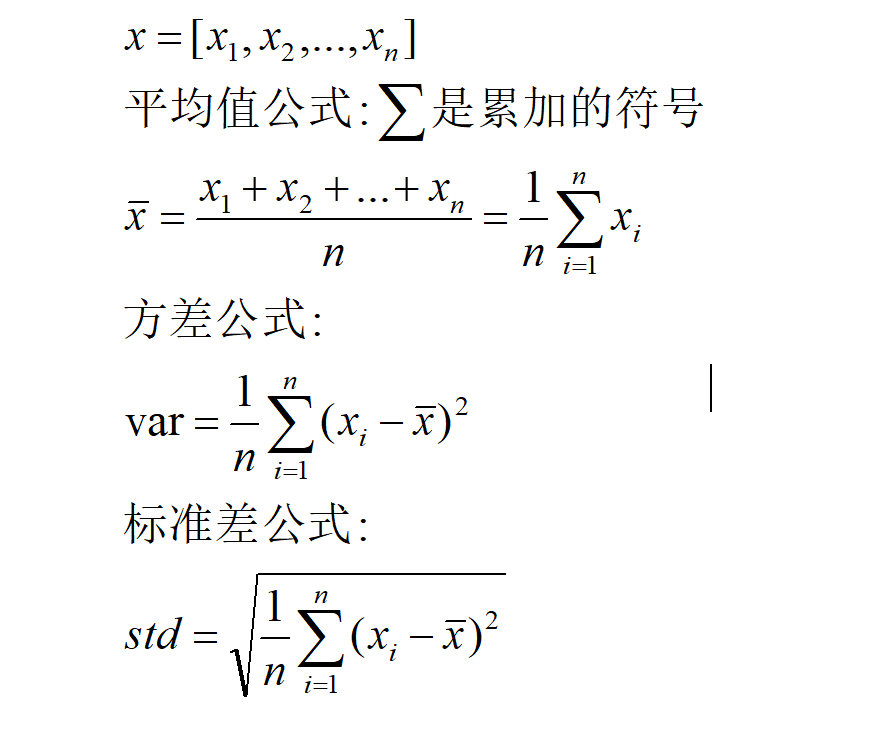Numpy包常用科学计算方法总结
numpy包的计算性能是python原始方法计算性能的几十倍到几百倍
一、引入numpy包:
import numpy as np二、创建数组:
#定义一个python的List
list = [1,2,3]
#将python的List包装成numpy的array:
array = np.array(list)
#array的类型为numpy.ndarray:
type(array) #numpy.ndarray
#array数组的维度是:
array.ndim # 1维数组,几维数组就返回几
#array的形状;
array.shape #(1,3) 代表1行3列
#array变形:
array.reshape(3,1) #将array改成3行1列。需要注意的是,reshape参数不能随便写,必须基于原有的数组,做有意义的变换,如何写的参数不对,基于array的原有数据不能进行reshape,会报错。三、利用np创建测试数据
#设置随机种子,设置成固定值后,np每次生成的随机数都是固定不变的
np.random.seed(1)
#生成随机数数组
np.random.randint(low = 0,high = 101,size=10)#表示生成从0(low)到100(不好含high)随机数数组,数组长度是10
np.random.randint(low = 0,high = 101,size = (2,5,3))#表示生成从0(low)到100(不好含high)随机数数组,生成的是一个三维数组,第一个维度有两个特征,第二个维度有5个特征,第三个维度有3个指标。可以这么形象的理解: 有两个班,每个班有5个学生,每个学生有3门课程。如何用数组表示两个班每个学生3门课程的成绩呢,就是这个表达式
incides = np.arange(num) #生成0至(num-1)个顺序数字的数组
np.random.shuffle(incides ) #将顺序数组打乱四、np常用计算公式
#np中array加减乘除一个数,都是在数组中每个元素上进行加减乘除这个数,如:
array = np.random.randint(low = 0,size = 101,size = (2,3))
#array([[91, 33, 38],[10, 77, 99]])
array+1
#array([[ 92, 34, 39],[ 11, 78, 100]])
array**2 # 平方
#array([[8281, 1089, 1444],[ 100, 5929, 9801]])
np.abs(array) #求每个元素的绝对值
np.sqrt(array) #求每个元素的开平方根
np.sin(array) #求每个元素的sin的值
array.sum(axis=0) #求array数组求和,axis=0代表求x轴总和,即各行的元素纵向相加,axis=1代表求y轴总和,即横向求和。默认不写则求所有元素的和。
#例如:
a = np.array([[1,2,3],[4,5,6]])
a.sum() #所有元素求和,21
a.sum(axis=0) # 求x轴的和,即每行的x轴对应相加,为array([5, 7, 9])
a.sum(axis=1) #求y轴的和,即横向相加构成y轴的一个值,为array([ 6, 15])
array.mean()# 求平均值,参数同sum()方法
array.std() #求标准差,参数同sum()五、向量与向量之间的计算
1. 向量的大小(向量的模)
a:[x1,x2,......xn] 公式:
#例如:
array = np.array([[1,2,3],[4,5,6]])
#求各元素的平方和:
a= (array**2).sum(axis=0)
# 再开根号就是array向量的模
np.sqrt(a)
#以上是手动求解,np提供了直接的求模方法: linalg是线性处理数据的工具包,就是线性代数相关的功能
np.linalg.norm(array)2.求两个向量的内积
公式:(a:[x1,x2,......xn] b:[y1,y2......yn]) (疑问: 多维数组的a和b如何表示呢?)
a = np.array([1,2,3])
b = np.array([4,5,6])
#内积的三种写法:
a @ b
a.dot(b)
np.dot(a,b)内积的含义:
3.求两个向量的余弦相似度
由上面公式可知,余弦相似度取值范围是[-1,1],是内积公式的变形。余弦相似度是两个向量的夹角,夹角越小越相似。
a = np.array([1,2,3])
b = np.array([4,5,6])
#余弦相似度:
a @ b /(np.linalg.norm(a)*np.linalg.norm(b))4.求两个向量的欧式距离
公式: d = sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2 +....)
表示两个向量之间的距离,距离越小,越相似
a = np.array([4,5,6])
b = np.array([1,2,3])
np.sqrt((a-b)**2)5. 方差、标准差公式
6. broadcast 广播机制
两个同维度的向量加减乘除运算可以直接对位运算。对于不同维度的两个向量,能否直接运算,需要看低维度的向量能否通过广播机制转成高维度的向量。所谓的广播机制就是通过复制行和列,使两个向量对齐,然后进行加减乘除计算。
六、练习应用
现在有50个同学,每个同学3门课程成绩,用np随机生成50名同学的成绩数组:
array = np.random.randint(low = 0,high = 101,size = (50,3))求三号同学的第2门成绩:
array[2,1]取出所有语文成绩不及格的同学:
#获取所有行所有列的写法:
array[:,:] # 第一个:代表所有行,第二个:代表所有列
#获取语文成绩小于60的学生成绩,也就是所有行是语文成绩小于60,列是所有列,写法如下:
array[array[:,0]<60,:]找出所有语文成绩及格但是英语成绩不及格的学生:
array[(array[:,0]>60 & array[:,2]<60),:]所有学生,所有成绩的平均分:
array.mean所有学生,每门课程的平均分,标准差:
array.mean(axis=0)
array.std(axis=0)