Day25|leetcode 216.组合总和III、17.电话号码的字母组合

leetcode 216.组合总和III

题目链接：216. 组合总和 III - 力扣（LeetCode）

视频链接：和组合问题有啥区别？回溯算法如何剪枝？| LeetCode：216.组合总和III_哔哩哔哩_bilibili

题目概述

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

1.只使用数字1到9。
2.每个数字 最多使用一次 。
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

思路

要分清集合和排列的区别，集合不分顺序，排列分顺序。

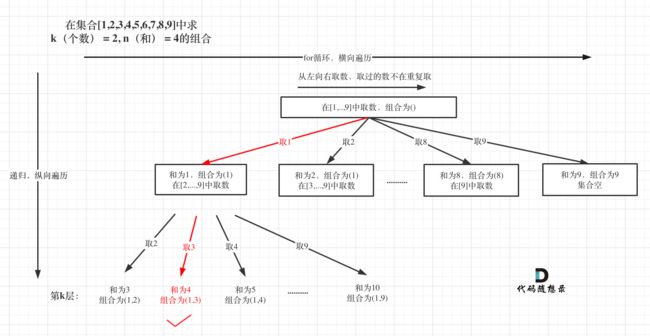
读完题首先需要画个图（可以把回溯想象成一个n叉树），这样思路会更清晰。这道题说白了就是在集合[1-9]中找个数（k）相加=和（n）的组合，由此不难画出二叉树，如图所示：

以k=2，n=4为例：

依旧根据回溯三部曲来写，其实理解了77.组合，这道题也不难理解。 

代码实现

targetSum是题目中的n。

k是集合里的个数。

sum是已经收集的元素的总和，也就是path里元素的总和。

startIndex是下一层for循环搜索的起始位置。

class Solution {
private:
    vector> result;
    vector path;
    void backtracking(int targetSum,int k,int sum,int startIndex) {
        if(path.size() == k) {
            if(sum == targetSum) result.push_back(path);
                return;
        }
        for(int i = startIndex;i <= 9;i++) {
            sum += i;
            path.push_back(i);
            backtracking(targetSum,k,sum,i + 1);
            sum -= i;
            path.pop_back();
        }
    }
public:
    vector> combinationSum3(int k, int n) {
        backtracking(n,k,0,1);
        return result;

    }
};

sum加完再减掉的原因就是为了让下一个元素上位，必须要减掉。

剪枝优化

这道题也能剪枝，如图所示：

我的上篇文章说过，剪枝优化的思路之一，经常性会想到的就是在范围上动手脚， 

 优化后的代码：

class Solution {
private:
    vector> result; // 存放结果集
    vector path; // 符合条件的结果
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (sum > targetSum) { // 剪枝操作
            return; // 如果path.size() == k 但sum != targetSum 直接返回
        }
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { // 剪枝
            sum += i; // 处理
            path.push_back(i); // 处理
            backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
            sum -= i; // 回溯
            path.pop_back(); // 回溯
        }
    }

public:
    vector> combinationSum3(int k, int n) {
        result.clear(); // 可以不加
        path.clear();   // 可以不加
        backtracking(n, k, 0, 1);
        return result;
    }
};

leetcode 17.电话号码的字母组合

题目链接：17. 电话号码的字母组合 - 力扣（LeetCode）

视频链接：还得用回溯算法！| LeetCode：17.电话号码的字母组合_哔哩哔哩_bilibili

题目概述

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

思路

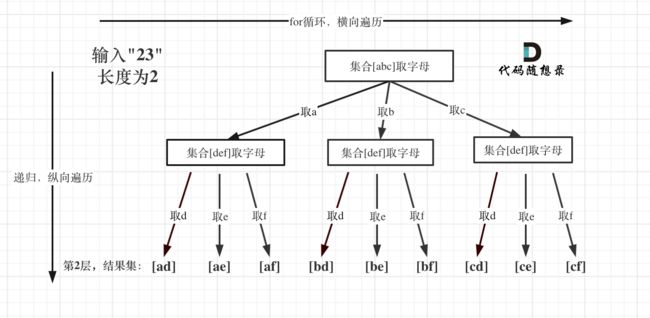
这道题是让输入数字，然后输出的是所输入数字对应的字母的映射，要考虑如何映射，同时也要考虑异常等情况，本题依旧使用回溯，因为一层for循环能写，两层for循环也能写，但要是30层、50层for循环呢，那就会崩溃吧，所以还是使用回溯。

如图所示：

 用字符串收集最终结果，用字符串数组保存起来，本题用的是index，而不是startIndex了，这个index是记录遍历第几个数字了，是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度，本题是求不同集合间的组合，每个数字都是一个集合。

代码实现

class Solution {
private:
    const string letterMap[10] = {
        "", // 0
        "", // 1
        "abc", // 2
        "def", // 3
        "ghi", // 4
        "jkl", // 5
        "mno", // 6
        "pqrs", // 7
        "tuv", // 8
        "wxyz", // 9
    };
public:
    vector result;
    string s;
    void backtracking(const string& digits, int index) {
        if (index == digits.size()) {
            result.push_back(s);
            return;
        }
        int digit = digits[index] - '0';        // 将index指向的数字转为int
        string letters = letterMap[digit];      // 取数字对应的字符集
        for (int i = 0; i < letters.size(); i++) {
            s.push_back(letters[i]);            // 处理
            backtracking(digits, index + 1);    // 递归，注意index+1，一下层要处理下一个数字了
            s.pop_back();                       // 回溯
        }
    }
    vector letterCombinations(string digits) {
        s.clear();
        result.clear();
        if (digits.size() == 0) {
            return result;
        }
        backtracking(digits, 0);
        return result;
    }
};

自己的收获：

听完昨天77.组合的课的时候，还有点感觉懵懵懂懂的，说不会吧，还能听明白，还能自己说出来，说不明白吧，还总感觉哪里好像没到位似的，但是今天听完课，就突然感觉自己稍稍的上了点道，希望自己二刷三刷的时候能悟的更多。ฅʕ•̫͡•ʔฅ