三、数学建模之非线性规划
1、定义
2、例题matlan代码求解
一、定义
1.非线性规划(Nonlinear Programming,简称NLP)是一种数学优化问题的方法,它处理的目标函数或约束条件包含非线性项。与线性规划不同,非线性规划涉及到在非线性约束下寻找最优解。在许多领域都有广泛的应用,包括工程、经济学、物流、金融等。它可以用来解决各种实际问题,例如生产优化、投资组合优化、工程设计等。然而,非线性规划问题通常比线性规划更复杂,求解过程可能会遇到局部最优解、数值不稳定性等挑战,因此需要仔细的问题建模和合适的数值技术来处理。
2.非线性规划问题的一般形式可以表示为:
这种问题的解决可以借助数学优化算法,例如梯度下降、拟牛顿法、全局优化算法等。选择适当的算法通常取决于问题的性质、约束条件的复杂性以及求解的精度要求。
3.与线性规划区别和特点
(1)目标函数与约束条件的线性性质:
线性规划:目标函数和约束条件都是线性的,这意味着变量之间的关系是线性的,例如:ax + by + cz。
非线性规划:允许目标函数和/或约束条件包含非线性项,如平方项、指数项、对数项等,这使得问题更加复杂。
(2)算法的差异:
线性规划:问题有高效的解决方法,例如单纯形法。这些方法通常能够在多项式时间内找到最优解。
非线性规划:问题通常需要更复杂的优化算法,如梯度下降、拟牛顿法、遗传算法等。这些算法的性能可能受到问题的特性和初始猜测的影响,求解时间也可能较长。
(3)解的性质:
线性规划:问题的解(如果存在)要么是唯一的最优解,要么是无解或者无穷多解(非有界问题)。这使得线性规划问题相对容易分析。
非线性规划:问题通常具有多个局部最优解,而全局最优解则需要更多的计算资源和策略来寻找。因此,非线性规划问题的解空间通常更复杂。
(4)应用领域:
线性规划:常用于资源分配、生产计划、运输问题等,这些问题通常可以很好地用线性模型描述。
非线性规划:更适用于那些涉及到非线性现象的问题,如曲线拟合、投资组合优化、工程设计等。
4.非线性规划问题不同特性和约束条件进行分类
(1)有约束非线性规划:
这是最常见的非线性规划问题,它包含一个或多个等式约束和/或不等式约束。问题的目标是在满足这些约束条件的情况下,找到目标函数的最小值。
(2)无约束非线性规划:
这类问题没有约束条件,只有一个目标函数需要最小化。在这种情况下,寻找函数的局部最小值成为主要挑战。
(3)半无约束非线性规划:
这种问题通常包含一个或多个整数变量和连续变量,并且有约束条件。其中一些变量必须是整数,而其他变量可以是连续的。这使得问题更加复杂,因为它涉及到混合整数规划和非线性规划的结合。
(4)混合整数非线性规划:
在这种问题中,目标函数和/或约束条件包含非线性项,并且问题还包含整数变量和连续变量。这是一类非常复杂的优化问题,需要专门的算法和技术来处理。
(5)全局非线性规划:
大多数非线性规划算法寻找局部最小值,而不是全局最小值。全局非线性规划问题的目标是找到目标函数的全局最小值,这通常更具挑战性,需要使用全局优化算法,如遗传算法、模拟退火等。
(6)多目标非线性规划:
这种问题涉及多个冲突的目标函数,需要找到一组解,以在多个目标之间达到平衡。解的集合称为 Pareto 前沿。
(7)凸非线性规划:
在凸非线性规划中,目标函数和所有约束条件都是凸函数。这类问题通常较容易求解,因为凸优化问题有良好的性质。
(8)非凸非线性规划:
这种问题中,目标函数和/或约束条件至少包含一个非凸函数。非凸问题通常更具挑战性,因为它们可能具有多个局部最优解。
5.解非线性规划问题方法和步骤
步骤 1:问题建模
定义目标函数: 首先,明确定义一个需要最小化或最大化的目标函数。这个函数通常是关于决策变量的非线性函数。
确定约束条件: 确定问题的约束条件,包括等式约束和不等式约束。约束条件是限制问题解的函数,它们必须被满足。
定义变量范围: 如果适用,定义决策变量的范围(上下界)。这些范围可以帮助缩小搜索空间。
步骤 2:选择求解方法
选择优化算法: 根据问题的性质、约束条件和求解要求选择适当的优化算法。常见的算法包括梯度下降、拟牛顿法、全局优化算法等。
初始化: 为决策变量选择初始值。初始值的选择可以影响算法的性能,因此需要谨慎。
步骤 3:
迭代优化: 使用所选的优化算法进行迭代优化。算法会在每个迭代步骤中根据目标函数和约束条件的梯度信息来更新决策变量,逐渐接近最优解。
步骤 4:
结果分析:最终得到的解是否满足问题的要求。检查目标函数值是否足够接近最优解,以及约束条件是否得到满足。
补充:
梯度下降法:梯度下降法是一种迭代方法,用于最小化目标函数。它基于目标函数的梯度(导数)来沿着下降最快的方向更新变量,以逐步减小目标函数值。
梯度下降法有多个变种,包括批量梯度下降、随机梯度下降和小批量梯度下降。选择哪种变种取决于问题的规模和性质。
拟牛顿法:拟牛顿法是一种迭代方法,通过估计目标函数的Hessian矩阵(二阶导数矩阵)的逆来更新变量。它在许多情况下比梯度下降法更快收敛。
BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法是拟牛顿法的一个常用变种。
全局优化方法:对于非凸问题或多模态问题,全局优化方法可以寻找目标函数的全局最优解,而不仅仅是局部最优解。这包括遗传算法、模拟退火、粒子群算法等。
约束优化方法:对于带约束条件的非线性规划问题,可以使用约束优化方法,如罚函数法、拉格朗日乘子法或内点法来处理约束。
内点法特别适用于大规模非线性规划问题。
二、几种例题和matlab求解代码
function f=fun1(x);
f=sum(x.^2)+8;
编写M函数fun2.m定义非线性约束条件
function [g,h]=fun2(x);
g=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束
h=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3]; %非线性等式约束
编写主程序文件如下
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')
2.无约束问题的matlab求解
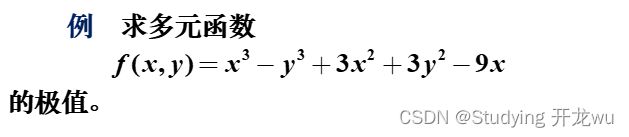
计算的Matlab程序如下
clc, clear
syms x y
f=x^3-y^3+3*x^2+3*y^2-9*x;
df=jacobian(f); %求一阶偏导数
d2f=jacobian(df); %求Hessian阵
[xx,yy]=solve(df) %求驻点
xx=double(xx);yy=double(yy);
for i=1:length(xx)
a=subs(d2f,{x,y},{xx(i),yy(i)});
b=eig(a); %求矩阵的特征值
f=subs(f,{x,y},{xx(i),yy(i)});
if all(b>0)
fprintf('(%f,%f)是极小值点,对应的极小值为%f\n',xx(i),yy(i),f);
elseif all(b<0)
fprintf('(%f,%f)是极大值点,对应的极大值为%f\n',xx(i),yy(i),f);
elseif any(b>0) & any(b<0)
fprintf('(%f,%f)不是极值点\n',xx(i),yy(i));
else
fprintf('无法判断(%f,%f)是否是极值点\n',xx(i),yy(i));
end
end
h=[4,-4;-4,8];
f=[-6;-3];
a=[1,1;4,1];
b=[3;9];
[x,value]=quadprog(h,f,a,b,[],[],zeros(2,1))
4.利用梯度求解约束优化问题matlab

函数fun10.m定义目标函数及梯度函数
function [f,df]=fun10(x);
f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
df=[exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+8*x(1)+6*x(2)+1);exp(x(1))*(4*x(2)+4*x(1)+2)];
函数fun11.m定义约束条件及约束条件的梯度函数
function [c,ceq,dc,dceq]=fun11(x);
c=[x(1)*x(2)-x(1)-x(2)+1.5;-x(1)*x(2)-10];
dc=[x(2)-1,-x(2);x(1)-1,-x(1)];
ceq=[];dceq=[];
写主程序文件如下
options=optimset('GradObj','on','GradConstr','on');
[x,y]=fmincon(@fun10,rand(2,1),[],[],[],[],[],[],@fun11,options)



