AtCoder Beginner Contest 313 C 一个序列同时加一个数和减一个数，直到最大和最小之间相差最大为1（结论可记住）

AtCoder Beginner Contest 313 C 

做题链接：AtCoder Beginner Contest 313

问题陈述

给你一个整数序列 A=(A1​,A2​,…,AN​)。你可以执行以下操作任意次数（可能为零）。

• 选择带有 1≤i,j≤N的整数 i和 j。将Ai​减少 1，将Aj​增加 1。

求使A的最小值与最大值之差最多为 1 所需的最小运算次数。

#### 输入

输入内容由标准输入法提供，格式如下
N
A_1 A_2 ... A_N

#### 输出

将答案打印为整数。

 

思想：1.给定一个固定的B，求使A等于B所需的最小运算次数

           2.在所有最大值和最小值最多相差1的B中，找出一个所需的运算次数最少的，即1

做法：

1.设S是所有k(1<=k<=n)中|ak-bk|的和，在一次操作中， 减少ai会使s改变1，增加aj也会改变1，因此，一次操作最多会使s减少两个，现在，我们的目标是使A等于B，即s=0，因此显然至少需要s/2次操作，并且我们总是可以通过s/2次运算使A=B（证明，如果增加一个数而没有对应的数来减，那就说明A的元素的和>B的元素的和，假设不成立）。因此，这个问题的答案是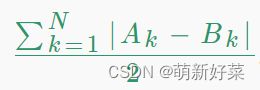

2.在所有最大值和最小值最多相差1的B中，找出一个所需运算次数最少的

步骤如下：

首先为了使B的元素之和=A的元素之和，且B的最大值和最小值最多相差1

那么B必须由p的（n-r）份和 (p+1)的r份组成，其中p和r分别是A的元素之和和除以n时的商和余数

题目问题可以简化为：在由p的（n-r）份和（p+）的r份组成的B中，找出一个所有|ak-bk|最小的

直觉上，当i=1,2...n按照Ai的升序排序时，让Bi=p代表i的前（n-r）个实例，让Bi=p+1代表i的后r个实例似乎是最优的。（证明：如果有AiBj），那么交换Bi和Bj不会增加|Ai-Bi|+|Aj-Bj|，这可以简单的按照Ai,Aj,Bi,Bj,的排序来划分情况

另外：时间复杂度为O(nlogn)，我们可以选择std::nth_element 在O(n)的时间内解决。

代码： 

// Problem: C - Approximate Equalization 2
// Contest: AtCoder - AtCoder Beginner Contest 313
// URL: https://atcoder.jp/contests/abc313/tasks/abc313_c
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include
using namespace std;

typedef long long ll;

const int N = 2e5+5;

int n;
int a[N];

int main(){
	cin>>n;
	vector a(n);
	ll sum=0;
	
	for(int i=0;i>a[i];
		sum+=a[i];
	}
	sort(a.begin(),a.end());
	vector b(n,sum/n);  //空间为n,初始值为sum/n
	for(int i=0;i