26.篮球练习
目录
题目
Description
Input
Output
Hint
思路
注意事项
C++完整代码(含注释)
题目
Description
小徐酷爱打篮球,在小学期的前两周半都在练习篮球。
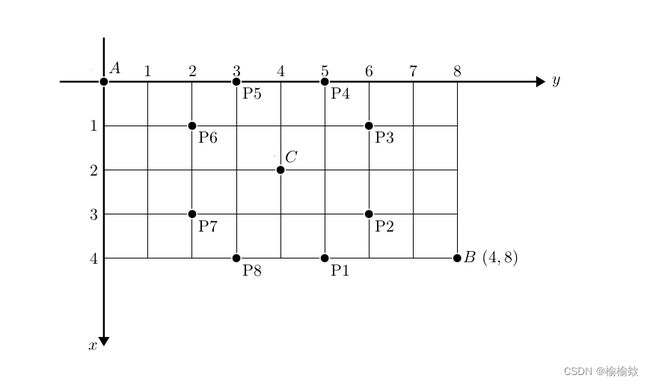
今天,小徐想要练习如何突破。练习场地可由如下所示的网格图表示,图中的位置可用坐标表示。
其中A点(0,0)为小徐的起始位置,B点(n,m)为小徐想要到达的位置。
一起训练的还有场上的防守队员小彩,其位于C点。已知小徐行动时只能向右或向下前进,且当小徐相对于小彩的位置为Pi(i = 1,2…8)时,小徐会被抢断。
注意,Pi坐标是会随C位置的变化而变化的,但相对位置是固定的
现在要求你计算小徐从A点到达B点且不被抢断的路径条数。假设小彩的位置是固定不动的,并不是小徐走一步小彩走一步。
Input
一行四个正整数,分别表示B点坐标和C点坐标。
Output
一个整数,表示所有的路径条数。
Hint
对于全部的数据,1≤n,m≤20,0≤ C点的横纵坐标 ≤20。
思路
我们需要计算小徐从起点A到达目标点B且不被小彩抢断的路径条数。
为了求解这个问题,我们可以将问题划分为子问题:小徐从起点到达每个格子的路径条数。
第一步:确定dp数组以及下标的含义
我们使用一个二维数组dp来表示路径数。
dp[i][j]表示小徐从起点A(0,0)到达位置(i,j)的路径数。
根据题目要求,当小徐相对于小彩的位置为Pi时,小徐会被抢断。
我们需要排除这些情况,即不能走到会被小彩抢断的位置上。
第二步:确定递推公式
小徐只能向右或向下前进。对于每个位置(i,j),小徐可以从上方格子(i-1,j)或左方格子(i,j-1)到达。
因此,状态转移方程为:dp[i][j] = dp[i-1][j] + dp[i][j-1]。
第三步:dp数组初始化
根据题目要求,小徐不能从起点A直接到达可能被小彩抢断的位置。因此,我们需要将这些位置的路径数初始化为 0。
- 如果小彩的位置恰好是起点A,则路径数为
0,即dp[0][0] = 0。 - 如果小彩相对于起点A的位置可以导致被抢断,那么小徐在起点的时候就已经被抢断了,这种情况下路径数也为
0。
第四步:确定遍历顺序
①两次一层for循环:
首先,我们需要遍历第一行和第一列,初始化每个格子的路径数。这是因为在动态规划的过程中,我们需要利用上一行和左一列的路径数来计算当前格子的路径数。
对于每个格子 (0, i)和(j, 0),我们检查小彩的位置是否与当前格子相同和是否会被抢断。
如果是,当前和之后位置的路径数都为 0;
如果都没有被抢断或遇到小彩的情况,路径数则都等于1。
②一次两层for循环:
对于其他格子 (i, j),我们需要考虑小彩的位置对路径数的影响,排除被抢断的情况。如果小彩的位置和当前格子位置相同,或者其相对位置会导致抢断,我们跳过当前格子,continue到下一个格子。否则,路径数等于上边格子 (i-1, j) 和左边格子 (i, j-1) 路径数之和。
第五步:结果处理
当计算到达目标点B(n,m)的路径数时,dp[n][m]即为所求的结果,即小徐从起点到达目标点且不被抢断的路径条数。
注意事项
使用long long存储数据,避免溢出。
C++完整代码(含注释)
有查重,记得修改!!
#include
using namespace std;
int main() {
long long Bx, By, Cx, Cy;
cin >> Bx >> By >> Cx >> Cy; // 读取目标点和小彩的坐标
long long dp[21][21] = { 0 }; // 定义一个二维数组来存储路径数
// 初始化起点的路径数为1
if ((Cx == 0 && Cy == 0) || (abs(0 - Cx) == 2 && abs(0 - Cy) == 1) || (abs(0 - Cx) == 1 && abs(0 - Cy) == 2))
dp[0][0] = 0;
else
dp[0][0] = 1;
// 遍历第一行,计算每个格子的路径数
for (int i = 1; i <= By; i++) {
if (0 == Cx && i == Cy) { // 如果小彩的位置和当前格子位置相同,则路径数为0
dp[0][i] = 0;
}
else if ((abs(0 - Cx) == 2 && abs(i - Cy) == 1) || (abs(0 - Cx) == 1 && abs(i - Cy) == 2)) { // 如果小彩相对位置存在抢断的情况,则路径数为0
dp[0][i] = 0;
}
else {
dp[0][i] = dp[0][i - 1]; // 否则,路径数等于左边格子的路径数
}
}
// 遍历第一列,计算每个格子的路径数
for (int i = 1; i <= Bx; i++) {
if (i == Cx && 0 == Cy) { // 如果小彩的位置和当前格子位置相同,则路径数为0
dp[i][0] = 0;
}
else if ((abs(i - Cx) == 2 && abs(0 - Cy) == 1) || (abs(i - Cx) == 1 && abs(0 - Cy) == 2)) { // 如果小彩相对位置存在抢断的情况,则路径数为0
dp[i][0] = 0;
}
else {
dp[i][0] = dp[i - 1][0]; // 否则,路径数等于上面格子的路径数
}
}
// 填充剩余格子的路径数
for (int i = 1; i <= Bx; i++) {
for (int j = 1; j <= By; j++) {
if (i == Cx && j == Cy) { // 如果小彩的位置和当前格子位置相同,则路径数为0
continue;
}
else if ((abs(i - Cx) == 2 && abs(j - Cy) == 1) || (abs(i - Cx) == 1 && abs(j - Cy) == 2)) { // 如果小彩相对位置存在抢断的情况,则路径数为0
continue;
}
else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; // 否则,路径数等于上面格子和左边格子路径数之和
}
}
}
cout << dp[Bx][By] << endl; // 输出到达目标点的路径数
return 0;
}