Day64｜图part3：695. 岛屿的最大面积、1254. 封闭岛屿的数量、1020. 飞地的数量

695. 岛屿的最大面积

leetcode链接：力扣题目链接

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿 是由一些相邻的 1 (代表土地) 构成的组合，
这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。
你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

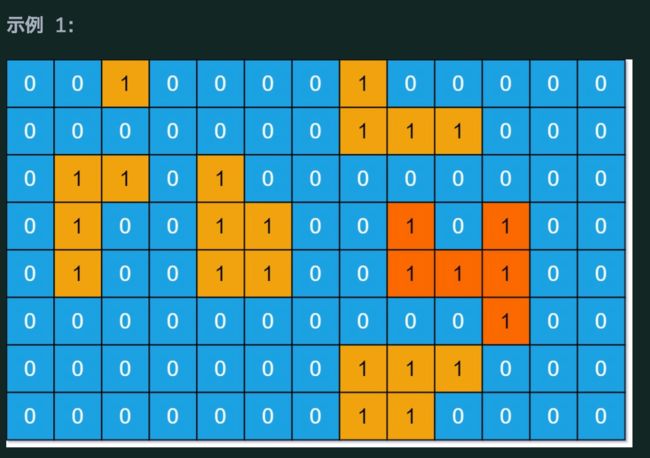
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],
  [0,0,0,0,0,0,0,1,1,1,0,0,0],
  [0,1,1,0,1,0,0,0,0,0,0,0,0],
  [0,1,0,0,1,1,0,0,1,0,1,0,0],
  [0,1,0,0,1,1,0,0,1,1,1,0,0],
  [0,0,0,0,0,0,0,0,0,0,1,0,0],
  [0,0,0,0,0,0,0,1,1,1,0,0,0],
  [0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

DFS

本题在dfs进行淹没岛屿的时候，除了淹没以外，还要想办法把岛屿的面积统计出来。

首先看下昨天的求岛屿数量的DFS代码：

class Solution {
public:
    void dfs(vector<vector<char>> &grid, int i, int j ){
        if (i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size()) {
            // 超出索引边界
            return;
        }
        if (grid[i][j] == '0') {
            // 已经是海水了
            return;
        }
        // 将 (i, j) 变成海水
        grid[i][j] = '0';
        // 淹没上下左右的陆地
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);

    }
    int numIslands(vector<vector<char>>& grid) {
        int res = 0;
        for(int i = 0; i < grid.size(); i++){
            for(int j = 0; j < grid[0].size(); j++){
                if(grid[i][j] == '1'){
                    res++;
                  dfs(grid,i,j);
                  
                }
            }
        }
        return res;
    }
};

这里可以把DFS改造成又返回值的：

    int dfs(vector<vector<int>> &grid, int i, int j ){
        if (i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size()) {
            // 超出索引边界
            return 0;
        }
        if (grid[i][j] == 0) {
            // 已经是海水了
            return 0;
        }
        // 将 (i, j) 变成海水
        grid[i][j] = 0;
        // 淹没上下左右的陆地
        return dfs(grid, i + 1, j)
        + dfs(grid, i, j + 1)
        + dfs(grid, i - 1, j)
        + dfs(grid, i, j - 1) + 1;

    }

也就是在淹岛的时候同时向四方搜寻，然后加起来，记得最后+1，否则递归中结果永远都是0。

最终代码：

class Solution {
public:
    int dfs(vector<vector<int>> &grid, int i, int j ){
        if (i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size()) {
            // 超出索引边界
            return 0;
        }
        if (grid[i][j] == 0) {
            // 已经是海水了
            return 0;
        }
        // 将 (i, j) 变成海水
        grid[i][j] = 0;
        // 淹没上下左右的陆地
        return dfs(grid, i + 1, j)
        + dfs(grid, i, j + 1)
        + dfs(grid, i - 1, j)
        + dfs(grid, i, j - 1) + 1;

    }
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int res = 0;//此时的res用来记录的是岛屿的最大面积。
        for(int i = 0; i < grid.size(); i++){
            for(int j = 0; j < grid[0].size(); j++){
                if(grid[i][j] == 1){//如果是岛
                    res = max(res, dfs(grid, i , j));
                }
            }
        }
        return res;
    }
};

BFS

这里直接贴代码了，BFS没有递归，使用queue，感觉代码要复杂些：

class Solution {
private:
    int count;
    int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
    void bfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
        queue<int> que;
        que.push(x);
        que.push(y);
        visited[x][y] = true; // 加入队列就意味节点是陆地可到达的点
        count++;
        while(!que.empty()) {
            int xx = que.front();que.pop();
            int yy = que.front();que.pop();
            for (int i = 0 ;i < 4; i++) {
                int nextx = xx + dir[i][0];
                int nexty = yy + dir[i][1];
                if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界
                if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 节点没有被访问过且是陆地
                    visited[nextx][nexty] = true;
                    count++;
                    que.push(nextx);
                    que.push(nexty);
                }
            }
        }
    }
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
        int result = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (!visited[i][j] && grid[i][j] == 1) {
                    count = 0;
                    bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
                    result = max(result, count);
                }
            }
        }
        return result;
    }
};

1254. 封闭岛屿的数量

leetcode链接：「统计封闭岛屿的数目open in new window」

二维矩阵 grid 由 0 （土地）和 1 （水）组成。
岛是由最大的4个方向连通的 0 组成的群，封闭岛是一个 完全 由1包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

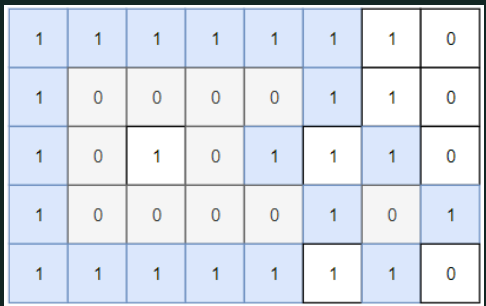
输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],
  [1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] 
输出：2 
解释： 灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

输入：grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
输出：1
示例 3：

输入：grid = [[1,1,1,1,1,1,1],
             [1,0,0,0,0,0,1],
             [1,0,1,1,1,0,1],
             [1,0,1,0,1,0,1],
             [1,0,1,1,1,0,1],
             [1,0,0,0,0,0,1],
             [1,1,1,1,1,1,1]]
输出：2

这题要注意和前面的题区分因为这里是1表示海水，0表示陆地！！！并且对岛屿的判断条件改成了封闭岛屿，所谓「封闭岛屿」就是上下左右全部被 1 包围的 0，也就是说靠边的陆地不算作「封闭岛屿」。

那么如何得到封闭岛屿？很简单，把前面的靠墙的岛屿排除掉，就是封闭岛屿了。

具体的做法就是在进行两层for循环的dfs之前，首先把四个边的岛屿都淹掉（淹掉的方法就是dfs）：

    int closedIsland(vector<vector<int>>& grid) {
        int res = 0;
        //首先先把边上的岛屿淹掉
        for(int i = 0; i < grid.size(); i++){
            dfs(grid, i,0);
            dfs(grid, i, grid[0].size() - 1);
        }
        for(int j = 0; j < grid[0].size();j++){
            dfs(grid, 0, j);
            dfs(grid,grid.size() - 1, j);
        }
        for(int i = 0; i < grid.size(); i++){
            for(int j = 0; j < grid[0].size(); j++){
                if(grid[i][j] == 0){
                    res++;
                    dfs(grid, i , j);
                }

            }
        }
        return res;
    }
};

最终代码：

class Solution {
public:
    void dfs(vector<vector<int>> &grid, int i, int j ){
        if (i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size()) {
            // 超出索引边界
            return;
        }
        if (grid[i][j] == 1) {
            // 已经是海水了
            return;
        }
        // 将 (i, j) 变成海水
        grid[i][j] = 1;
        // 淹没上下左右的陆地
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);

    }
    int closedIsland(vector<vector<int>>& grid) {
        int res = 0;
        //首先先把边上的岛屿淹掉
        for(int i = 0; i < grid.size(); i++){
            dfs(grid, i,0);
            dfs(grid, i, grid[0].size() - 1);
        }
        for(int j = 0; j < grid[0].size();j++){
            dfs(grid, 0, j);
            dfs(grid,grid.size() - 1, j);
        }

      
        for(int i = 0; i < grid.size(); i++){
            for(int j = 0; j < grid[0].size(); j++){
                if(grid[i][j] == 0){
                    res++;
                    dfs(grid, i , j);
                }

            }
        }
        return res;
    }
};

1020. 飞地的数量

leetcode链接：力扣链接

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

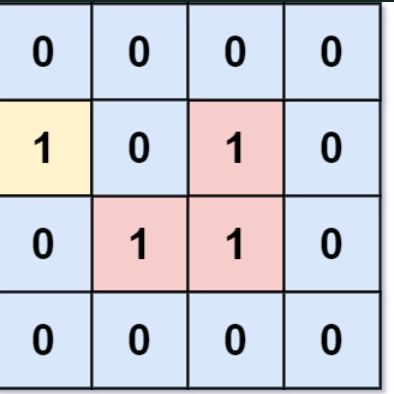
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]] 
  输出：3 解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

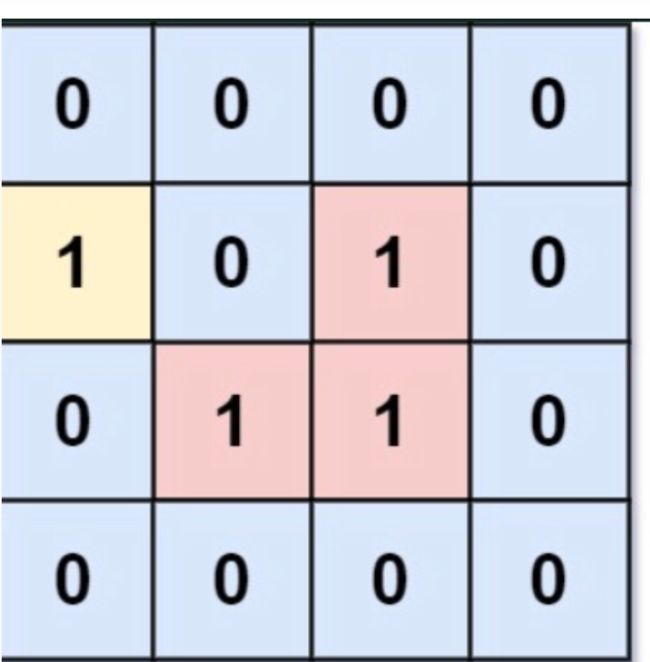
如何理解这里的飞地？

假设你站在这片海的边缘，你可以从边缘任意的点向岛屿移动，可以一步到达的岛就不是飞地，没办法一步到达的就是飞地。

比如这里的黄色岛，站在（2，1）就可以到达，而红色的岛站哪里都无法到达。所以返回这个岛的面积3.

跟之前封闭的岛屿数量其实是一样的，也是把边缘的岛淹了，然后这里注意不用再dfs进行淹岛了，因为这里统计的是1的数量：

int numEnclaves(vector<vector<int>>& grid) {
        //先把周围的岛淹了
        int m = grid.size(), n = grid[0].size();
        for(int i = 0; i < m; i++){
            dfs(grid, i,0);
            dfs(grid, i, n - 1);
        }
        for(int j = 0; j < n;j++){
            dfs(grid, 0, j);
            dfs(grid,m - 1, j);
        }
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1){
                    res++;
                }

            }
        }
        return res;
    }

最终代码（DFS都是一样的）：

class Solution {
public:
    int res = 0;
    void dfs(vector<vector<int>> &grid, int i, int j ){
        if (i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size()) {
            // 超出索引边界
            return;
        }
        if (grid[i][j] == 0) {
            // 已经是海水了
            return;
        }
        // 将 (i, j) 变成海水
        grid[i][j] = 0;
        // 淹没上下左右的陆地
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);

    }
    int numEnclaves(vector<vector<int>>& grid) {
        //先把周围的岛淹了
        int m = grid.size(), n = grid[0].size();
        for(int i = 0; i < m; i++){
            dfs(grid, i,0);
            dfs(grid, i, n - 1);
        }
        for(int j = 0; j < n;j++){
            dfs(grid, 0, j);
            dfs(grid,m - 1, j);
        }
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1){
                    res++;
                }

            }
        }
        return res;
    }
};

总结

• 岛屿问题，目前只会有DFS，BFS的解法二刷再过一遍
• 要注意题目的意思，是0是海水还是1是海水；grid是char数组还是int数组。