较难理解的字符串查找算法KMP

时间复杂度O(n)的子串查找算法。

经典实例

主字符串(s)：abcabcabd
模式串(t)：abcabd

比较次数    主字符串    模式串    备注
一    abcabcabd    abcabd    红色和绿色表示正在比较的子串，红色表示不同部分，绿色表示相同部分。
二    abcabcabd    abcabd    
三    abcabcabd    abcabd    
四    abcabcabd    abcabd    
五    abcabcabd    abcabd    
六    abcabcabd    abcabd    ab是abcab的公共前后缀，abcab是上次（第五次比较成功的子串）
七    bcab    abca    
八      cab    abc    
九      ab    ab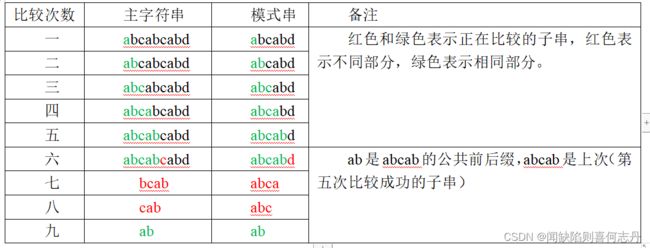    

观点：只需要比较上次相等部分的公共前后缀

假定一：s[i1...i2)等于t[0...j)
假定二：s[i2]不等于t[j]
假定二的意思是i1不是find的返回值。
假定三：x取[i1...i2)，字符串s[x...i2)的长度是len=i2-x。
假定一和假定三可以得出推理一：s[x,i2)等于t[j-len...j)。
结合推理一，如果t[0...j-len)不等于t[j-len,j)则t[0...j-len)不等于s[x...i2),也就是s[x...]不是find返回值。
结论一：如果t[0...j)长度为len的前缀和后缀不相等，则x不是结果，直接忽略。
结论二：如果t[0...j)长度为len的前缀和后缀相等,则t[x...j)和s[0...len)相等，直接比较t[j]和s[len)。
从最长公共前缀处理还是从最短公共前缀开始
i1递增的过程和从最长公共前缀到最短公共前缀的过程。

不需要记录所有公共前缀

只需要记录最长公共前缀，然后递归或迭代求。因为：次长公共前缀就是最长公共前缀的最长公共前缀。

说明

s[i,j)表示从i到j的子串，包括i不包括j。S[x...]表示从索引k开始的子串，长度未定。
字符串s[0,j)公共前后缀指的是s[0,x)等于s[j-x,j)，x不等于j，也就是公共前后缀必能是本身。
获取最长公共前后缀
如果s[0,j)的公共前缀为x，如果x大于0，则必定有s[0,j-1)的前缀为x-1。所以只需要比较s[0,j-1)的公共前后缀。

核心代码

class KMP
{
public:
    virtual int Find(const string& s,const string& t )
    {
        CalLen(t);
        m_vSameLen.assign(s.length(), 0);
        for (int i1 = 0,  j = 0; i1 < s.length(); )
        {
            for (; (j < t.length()) && (i1 + j < s.length()) && (s[i1 + j] == t[j]); j++);
            //i2 = i1 + j 此时s[i1,i2)和t[0,j)相等 s[i2]和t[j]不存在或相等
            m_vSameLen[i1] = j;
            //t[0,j)的结尾索引是j-1，所以最长公共前缀为m_vLen[j-1]，简写为y 则t[0,y)等于t[j-y,j)等于s[i2-y,i2)
            if (0 == j)
            {
                i1++;
                continue;
            }
            const int i2 = i1 + j;
            j = m_vLen[j - 1];
            i1 = i2 - j;//i2不变
        }
        
        for (int i = 0; i < m_vSameLen.size(); i++)
        {//多余代码是为了增加可测试性
            if (t.length() == m_vSameLen[i])
            {
                return i;
            }
        }
        return -1;
    }
protected:
    void CalLen(const string& str)
    {
        m_vLen.resize(str.length());
        for (int i = 1; i < str.length(); i++)
        {
            int next = m_vLen[i-1];
            while (str[next] != str[i])
            {
                if (0 == next)
                {
                    break;
                }
                next = m_vLen[0];
            }
            m_vLen[i] = next + (str[next] == str[i]);
        }
    }
    int m_c;
    vector m_vLen;//m_vLen[i] 表示t[0,i]的最长公共前后缀
    vector m_vSameLen;//m_vSame[i]记录 s[i...]和t[0...]最长公共前缀，增加可调试性
};

测试代码

class CTestKMP :public KMP
{
public:
    virtual int Find(const string& s, const string& t) override
    {
        int iRet = KMP::Find(s,t);
        for (int i = 0; i < m_vLen.size(); i++)
        {
            std::cout << t.substr(0, i + 1).c_str() << " " << m_vLen[i] << std::endl;
        }
        return iRet;
    }
    void Assert(const vector& vLen,const vector& vSameLen)
    {
        for (int i = 0; i < vLen.size(); i++)
        {
            assert(vLen[i] == m_vLen[i]);
        }
        for(int i = 0 ; i < vSameLen.size();i++)
        {
            assert(vSameLen[i] == m_vSameLen[i]);
        }
    }
};

int main()
{
    vector ss = { "abcabcabd","abc","abcb","cabaab"};
    vector ts = { "abcabd" ,"d","b","ab"};
    vector> lens = { {0, 0, 0, 1, 2, 0},{0},{0},{0,0} };
    vector> sameLens = { {5, 0, 0, 6, 0, 0,0,0,0},{0,0,0},{0,1,0,1},{0,2,0,1,2,0 } };
    for (int i = 0; i < ss.size(); i++)
    {
        CTestKMP kmp;
        auto res = kmp.Find(ss[i], ts[i]);
        kmp.Assert(lens[i], sameLens[i]);
    }
    
}

开发测试环境

Win10 VS2022

附

如果格式混乱影响阅读，请到CSDN下载word版。目前审核中，请稍候！

作者的话

KMP确实比较难理解，我学习了多次。并且重写了至少两次。希望这次是真懂了。