【Mo 人工智能技术博客】时序预测模型——LSTNet
时序预测模型——LSTNet
作者:陈东瑞
1. 背景
多元时间序列数据在我们的日常生活中无处不在,从股票市场的价格,高速公路上的交通流量,太阳能发电厂的输出量,不同城市的温度等等。 在这样的应用中,用户通常对基于时间序列的历史观察来对新趋势或潜在危险事件的进行预测。 例如,可以基于几个小时前的交通拥堵模式来设计更好的路线计划,通过预测将来股票市场来获得更大的收益。
在这些实际场景中的时间序列通常涉及长期和短期模式的混合,但传统方法(例如自回归模型和高斯过程)在处理这些问题时往往会失效。本文中,我们介绍一种针对多元时间序列预测而设计的深度学习框架——长期和短期时间序列网络(LSTNet),它可以有效解决长短期模式的混合问题。 LSTNet 使用卷积神经网络(CNN)和递归神经网络(RNN)来提取变量之间的短期局部依赖模式,并发现时间序列趋势的长期模式。此外,它利用传统的自回归模型来解决神经网络模型的规模不敏感问题。
2. 模型介绍
LSTNet利用卷积层的优势来发现局部多维输入变量和循环层之间的依赖关系模式,以捕获复杂的长期依赖关系。它通过一种新颖的递归结构(即递归跳跃)来捕获非常长期的依赖模式,并利用输入时间序列信号的周期性来简化优化过程。最后,LSTNet结合了与非线性神经网络部分并行的传统自回归线性模型,这使得非线性深度学习模型对于违反尺度变化的时间序列更具鲁棒性。该部分我们主要介绍LSTNet结构、目标函数和优化策略三个部分。
2.1 LSTNet结构
下图概述了LSTnet体系结构。 LSTNet是一个深度学习框架,专门设计用于混合了长期和短期模式的多元时间序列预测任务。我们将详细介绍LSTNet的构建基块:卷积单元、循环单元、循环跳远单元、时序注意单元、自回归单元。
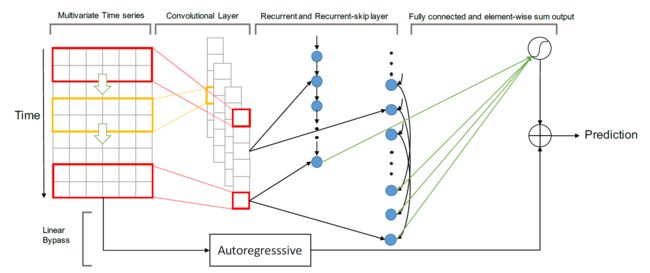
2.1.1 卷积部分
LSTNet 的第一层为卷积层,且没有池化层。它主要目的是提取时间维度中的短期模式以及变量之间的局部依存关系。 卷积层由宽度为 ω \omega ω,高度为 n n n(高度与变量数相同)的多个过滤器组成。 第k个滤波器扫过输入矩阵$X 并产生 并产生 并产生h_k$,
h k = R E L U ( W k ∗ X + b k ) (1) h_k = RELU(W_k * X +b_k) \tag{1} hk=RELU(Wk∗X+bk)(1)
其中 ∗ * ∗表示卷积运算,输出 h k h_k hk将是一个矢量,RELU 函数为: R E L U ( x ) = m a x ( 0 , x ) RELU(x) = max(0, x) RELU(x)=max(0,x)。 我们在输入矩阵 X X X的左侧通过零填充使长度为T的每个向量 h k h_k hk。卷积层的输出矩阵的大小为 d c × T d_c \times T dc×T,其中 d c d_c dc表示滤波器的数量。
2.1.2 循环部分
卷积层的输出同时作为循环单元和循环跳跃单元的输入。 循环单元是具有门控循环单元(GRU)的循环层,并使用RELU功能作为隐藏更新激活功能。循环单元的 t t t时刻的隐藏状态可以通过(2)式计算求得。
r t = σ ( x t W x r + h t − 1 W h r + b r ) u t = σ ( x t W x u + h t − 1 W h u + b u ) c t = R E L U ( x t W x c + r t ⊙ ( h t − 1 W h c ) + b c ) h t = ( 1 − u t ) ⊙ h t − 1 + u t ⊙ c t (2) {\begin{aligned} &r_t = \sigma(x_tW_{xr} +h_{t-1}W_{hr}+b_r)\\ &u_t = \sigma(x_tW_{xu} +h_{t-1}W_{hu}+b_u)\\ &c_t = RELU(x_tW_{xc} +r_t\odot(h_{t-1}W_{hc})+b_c)\\ &h_t = (1-u_t)\odot h_{t-1}+u_t \odot c_t\\ \end{aligned}}\tag{2} rt=σ(xtWxr+ht−1Whr+br)ut=σ(xtWxu+ht−1Whu+bu)ct=RELU(xtWxc+rt⊙(ht−1Whc)+bc)ht=(1−ut)⊙ht−1+ut⊙ct(2)
其中 ⊙ \odot ⊙是元素的乘积, σ \sigma σ是sigmoid函数, x t x_t xt是该层在 t t t时刻的输入,该层的输出是每个时刻的隐藏状态。根据经验,我们发现RELU作为激活函数可以提供更可靠的性能,从而使梯度更易于反向传播。
2.1.3 循环跳跃部分
尽管使用 GRU 和 LSTM 单元的循环层经过精心设计,通过记住历史信息,来解决长期的依赖性问题的。但是由于梯度消失的问题,实际上 GRU 和 LSTM 依然无法捕获非常长期的相关性。LSTNet 通过在当前隐藏单元和相同相位的隐藏单元之间添加跳过链接,来缓解此问题。即在相邻时段中,在当前隐藏单元和相同相位的隐藏单元之间添加跳过链接。 其更新过程可以表述为:
r t = σ ( x t W x r + h t − p W h r + b r ) u t = σ ( x t W x u + h t − p W h u + b u ) c t = R E L U ( x t W x c + r t ⊙ ( h t − p W h c ) + b c ) h t = ( 1 − u t ) ⊙ h t − p + u t ⊙ c t (3) {\begin{aligned} &r_t = \sigma(x_tW_{xr} +h_{t-p}W_{hr}+b_r)\\ &u_t = \sigma(x_tW_{xu} +h_{t-p}W_{hu}+b_u)\\ &c_t = RELU(x_tW_{xc} +r_t\odot(h_{t-p}W_{hc})+b_c)\\ &h_t = (1-u_t)\odot h_{t-p}+u_t \odot c_t\\ \end{aligned}}\tag{3} rt=σ(xtWxr+ht−pWhr+br)ut=σ(xtWxu+ht−pWhu+bu)ct=RELU(xtWxc+rt⊙(ht−pWhc)+bc)ht=(1−ut)⊙ht−p+ut⊙ct(3)
其中该层的输入是卷积层的输出, p p p是跳过的隐藏单元的数量。对于具有清晰周期性模式的数据,可以轻松确定 p p p 的值(例如,小时用电量和流量使用数据集, p = 24 p=24 p=24),否则必须进行调整。
之后我们通过一个全连接层,间循环层和循环跳跃层的输出整合在一起。全连接层的输入包包循环单元在t时刻的的隐藏状态和 p p p 个(从 t − p + 1 t-p+1 t−p+1 到 t t t)循环跳跃单元的隐藏状态。全连接层的输出计算过程为:
h t D = W R h t R + ∑ i = 0 p − 1 W i S h t − i S + b (4) h_t^D = W^Rh_t^R + \sum_{i = 0}^{p-1} {W_i^Sh_{t-i}^S +b} \tag{4} htD=WRhtR+i=0∑p−1WiSht−iS+b(4)
其中 h t D h_t^D htD是神经网络在t时刻的预测值。
2.1.4 时序注意层
由于循环跳跃层需要预定义的超参数p,这对周期性不明显或者周期不固定的序列是很不友好的。 为了减轻这种问题,LSTNet 引入了注意力机制,该机制学习输入矩阵每个窗口位置处隐藏表示的加权组合。 具体而言,将当前 t t t 时刻的注意力权重 α t ∈ R q \alpha_t \in \mathbb{R}^q αt∈Rq 计算为:
α t = A t t n S c o r e ( H t R , h t − 1 R ) \alpha_t = AttnScore(H_t^R, h_{t-1}^R) αt=AttnScore(HtR,ht−1R)
其中 H t R = [ h t − q R , . . . , h t − 1 R ] H_t^R = [h_{t-q}^R, ...,h_{t-1}^R] HtR=[ht−qR,...,ht−1R] 是一个矩阵,该矩阵按列堆叠 RNN 的隐藏表示,AttnScore是一些相似函数,例如点积,余弦或由简单的多层感知器参数化。时序注意层的最后输出是加权上下文向量 c t = H t α t c_t = H_t\alpha_t ct=Htαt与最后一个窗口隐藏表示 h t − 1 R h_{t-1}^R ht−1R的串联,以及线性投影算子。
h t D = W [ c t ; h t − 1 R ] + b h_t^D = W[c_t;h_{t-1}^R]+b htD=W[ct;ht−1R]+b
2.1.5 自回归部分
由于卷积和递归分量的非线性特性,神经网络模型的一个主要缺点是输出的大小对输入的大小不敏感。然而,在的真实数据中,输入信号的大小通常会以非周期的方式不断变化,这会大大降低神经网络模型的预测准确性。为了解决这一缺陷,LSTNet 模型将最终预测分解为线性部分和非线性部分。线性部分主要集中在局部尺度问题,非线性部分包含循环的特征。在LSTNet架构中,我们采用经典的自回归(AR)模型作为线性组件。将AR分量的预测结果表示为 h t L ∈ R n h_t^L \in \mathbb{R}^n htL∈Rn,并将AR模型的系数表示为 W a r ∈ R q a r W^{ar} \in \mathbb{R}^{q^{ar}} War∈Rqar和 b a r ∈ R b^{ar} \in \mathbb{R} bar∈R,其中 q a r q^{ar} qar是输入矩阵上输入窗口的大小。模型中,所有维度共享相同的线性参数。自回归模型展示如下:
h t , i L = ∑ k = 0 q a r − 1 W k a r y t − k , i + b a r (5) h_{t,i}^L = \sum_{k=0}^{q^{ar}-1}W_k^{ar}y_{t-k,i}+b^{ar} \tag{5} ht,iL=k=0∑qar−1Wkaryt−k,i+bar(5)
LSTNet 模型将神经网络和自回归模型的输出整合在一起作为最终的输出:
Y ^ t = h t D + h t L (6) \hat{Y}_t = h_t^D +h_t^L \tag{6} Y^t=htD+htL(6)
其中 Y ^ t \hat{Y}_t Y^t 是模型在 t t t 时刻最终的预测结果。
2.2 目标函数
在预测任务中,常用的目标函数就是平方误差,用公式表示为:
m i n i m i z e Θ ∑ t ∈ Ω T r a i n ∥ Y t − Y ^ t − h ∥ F 2 (7) \mathop{minimize}\limits_{\Theta} \sum_{t \in \Omega_{Train}}\left \| Y_t-\hat{Y}_{t-h}\right\|_F^2 \tag{7} Θminimizet∈ΩTrain∑ Yt−Y^t−h F2(7)
Θ \Theta Θ是模型的参数, Ω T r a i n \Omega_{Train} ΩTrain是训练集的时间集合, ∥ ∙ ∥ F \left \| \bullet \right\|_F ∥∙∥F是Frobenius范数, h h h是视野范围。具有平方损失函数的传统线性回归模型被称为线性岭,它等效于具有岭正则化的向量自回归模型。 但是,在某些数据集中,线性支持向量回归(Linear SVR)主导了Linear Ridge模型。 Linear SVR和Linear Ridge之间的唯一区别是目标函数。线性SVR的目标函数是
m i n i m i z e Θ 1 2 ∥ Θ ∥ + C ∑ t ∈ Ω T r a i n ∑ i = 0 n − 1 ξ t , i s u b j e c t t o ∣ Y ^ t − h , i − Y t , i ∣ ≤ ξ t , i + ϵ , t ∈ Ω T r a i n , ξ t , i ≥ 0 (8) { \begin{aligned} &\mathop{minimize}\limits_{\Theta} \frac{1}{2} \left\| \Theta \right\| +C \sum_{t \in \Omega_{Train}}\sum_{i=0}^{n-1}\xi_{t,i}\\ &subject\ to |\hat{Y}_{t-h,i}-Y_{t,i}| \leq \xi_{t,i} +\epsilon , t \in \Omega_{Train},\xi_{t,i} \ge 0 \end{aligned}}\tag{8} Θminimize21∥Θ∥+Ct∈ΩTrain∑i=0∑n−1ξt,isubject to∣Y^t−h,i−Yt,i∣≤ξt,i+ϵ,t∈ΩTrain,ξt,i≥0(8)
这里 C C C和 ϵ \epsilon ϵ是超参数。
受线性 SVR 模型出色性能的启发,我们将其目标函数纳入LSTNet模型中,以替代平方损失。 为简单起见,我们假设 ϵ = 0 1 \epsilon = 0^1 ϵ=01,并且上述目标函数减小为绝对损失(L1-loss)函数,如下所示:
m i n i m i z e Θ ∑ t ∈ Ω T r a i n ∑ i = 0 n − 1 ∣ Y t , i − Y ^ t − h , i ∣ (9) \mathop{minimize}\limits_{\Theta} \sum_{t \in \Omega_{Train}}\sum_{i=0}^{n-1}|Y_{t,i}-\hat{Y}_{t-h,i}| \tag{9} Θminimizet∈ΩTrain∑i=0∑n−1∣Yt,i−Y^t−h,i∣(9)
绝对损失函数的优点在于,它对真实的时间序列数据中的异常更加稳健。
2.3 优化策略
这里的优化策略与传统的时间序列预测模型相同。鉴于是一个回归问题,所以这里采用的是随机梯度下降(SGD)的方法。
3. 模型应用
论文对该方法进行了对比分析。
3.1 评价指标
这里使用的评价指标为RSE(Root Relative Squared Error )和 CORR(Empirical Correlation Coefficient)。具体计算如下:
R S E = ∑ ( i , t ) ∈ Ω T e s t ( Y i t − Y ^ i t ) 2 ∑ ( i , t ) ∈ Ω T e s t ( Y i t − m e a n ( Y ) 2 (10) RSE = \frac{\sqrt{\sum_{(i,t)\in \Omega_{Test}}(Y_{it}-\hat{Y}_{it})^2}}{\sqrt{\sum_{(i,t)\in \Omega_{Test}}(Y_{it}-mean(Y)^2}} \tag{10} RSE=∑(i,t)∈ΩTest(Yit−mean(Y)2∑(i,t)∈ΩTest(Yit−Y^it)2(10)
C O R R = 1 n ∑ i = 1 n ∑ t ( Y i t − m e a n ( Y i ) ) ( Y ^ i t − m e a n ( Y ^ i ) ) ∑ t ( Y i t − m e a n ( Y i ) ) 2 ( Y ^ i t − m e a n ( Y ^ i ) ) 2 (11) CORR = \frac{1}{n} \sum_{i=1}^{n} \frac{\sum_t(Y_{it}-mean(Y_i))(\hat{Y}_{it}-mean(\hat{Y}_i))}{\sqrt{\sum_t(Y_{it}-mean(Y_i))^2(\hat{Y}_{it}-mean(\hat{Y}_i))^2} }\tag{11} CORR=n1i=1∑n∑t(Yit−mean(Yi))2(Y^it−mean(Y^i))2∑t(Yit−mean(Yi))(Y^it−mean(Y^i))(11)
3.2 数据介绍
- 交通:加州交通运输部每小时收集48个月(2015-2016年)数据。 数据描述了由旧金山湾地区高速公路上的不同传感器测得的道路占用率(介于0和1之间)。
- 太阳能:2006年的太阳能发电记录,每10分钟从阿拉巴马州的137个光伏电站中采样一次。
- 电力:从2012年到2014年,每15分钟记录一次kWh的电力消耗,321位客户。 作者转换了数据以反映小时消耗;
- 汇率:收集1990年至2016年八个澳大利亚,英国,加拿大,瑞士,中国,日本,新西兰和新加坡等八个国家的每日汇率。
3.3 实验结果
文章中在 4 种基准数据集上使用 9 种方法进行了广泛的实验,模型的表现效果如下:
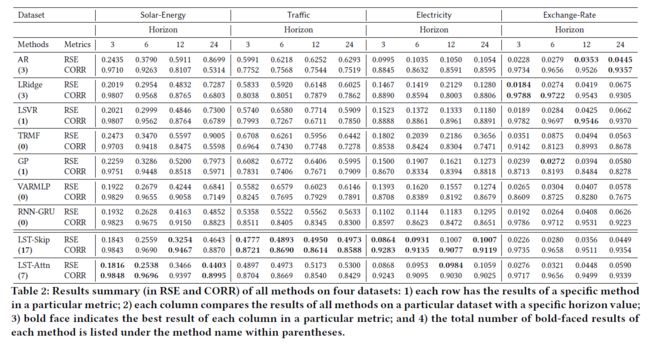
4. 模型实践
我们在momodel平台上fork了作者的代码,这里采用汇率的数据集。
项目地址:https://momodel.cn/explore/5dcd2380e44648e683935c30?type=app
参考资料
- Lai G, Chang W, Yang Y, et al. Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks[C]. international acm sigir conference on research and development in information retrieval, 2018: 95-104…
- LSTNet详解 https://zhuanlan.zhihu.com/p/61795416
关于我们
Mo(网址:https://momodel.cn)是一个支持 Python 的人工智能在线建模平台,能帮助你快速开发、训练并部署模型。
近期 Mo 也在持续进行机器学习相关的入门课程和论文分享活动,欢迎大家关注我们的公众号:MomodelAI获取新资讯!