论文笔记24:两篇注意力机制去噪文章
两篇注意力机制去噪文章
- Enhanced Non-Local Cascading Network with Attention Mechanism for Hyperspectral Image Denoising-网络比较复杂
-
- 引言
- 方法
- 实验
- 代码
- ADRN: Attention-based Deep Residual Network for Hyperspectral Image Denoising-对比上文的通道注意力块
-
- 引言
- 方法
Enhanced Non-Local Cascading Network with Attention Mechanism for Hyperspectral Image Denoising-网络比较复杂
引言
HDnTD、HSI-DeNet,然而,在这些方法中没有考虑HSI的空间光谱相关性。HSID-CNN也有一些缺点,例如,由于空间特征提取的不足,HSID-CNN在某些情况下不能很好地抑制HSI中的噪声。
方法
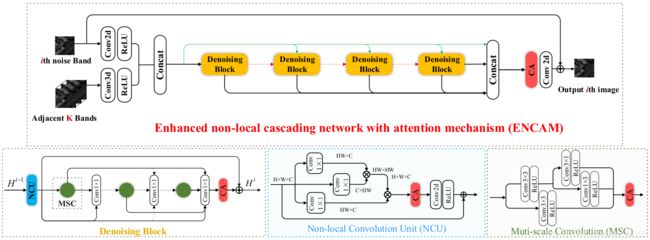
主去噪结构由几个去噪块组成,它们串联在一起提取高低频特征。同时,将第一层的浅层特征送入每个去噪块补充图像细节。在最后一层生成输出干净图像之前,应用通道注意力模块提取更多有用的特征映射。
损失函数为 L o s s = 1 2 N ∑ i = 1 N ∥ N e t ( y i , k i , θ ) − φ i ∥ 2 2 L o s s=\frac{1}{2 N} \sum_{i=1}^{N}\left\|N e t\left(y_{i}, k_{i}, \theta\right)-\varphi_{i}\right\|_{2}^{2} Loss=2N1∑i=1N∥Net(yi,ki,θ)−φi∥22
通道注意机制被用来增强通道间信号。使用全局平均和全局最大化处理来提取信号。
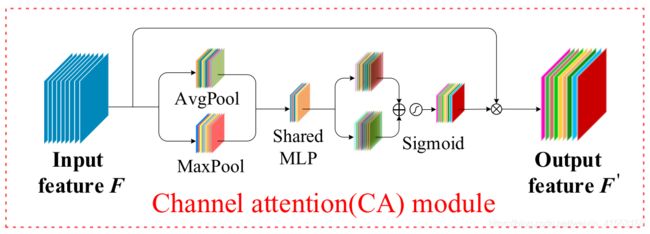
令 F a v g F_{avg} Favg和 F m a x F_{max} Fmax为平均池化特征和最大池化特征,通道注意力模型可以写为

NCU由非局部模块、通道注意力模块和卷积层组成,用于增强融合后的特征信号。当特征映射被送入每个去噪块时,首先由NCU进行处理,融合不同的特征映射。为了减少网络的参数,一个3×3的卷积层被分成1×3和3×1的卷积层。整个单元采用级联残差密集(cascading residual dense)结构,采用1×1卷积融合不同尺度特征。所以设 f M f_M fM为多尺度卷积函数, f τ f_τ fτ为融合1×1运算。整个去噪块计算如下(似乎有问题):
实验
数据集:
Washington DC Mall dataset
Pavia Centre dataset
Indian Pine dataset
Washington DC Mall dataset和Pavia Centre dataset的部分用于训练整个网络,其他部分用于测试。
参数设置:将训练数据集分成9650个大小为20×20的小块(patches)。两个测试数据库的K设置为30,Adam用于优化网络参数,动量参数分别为0.9、0.999和 1 0 − 8 10^{-8} 10−8. 整个模型的权重由[19]中的方法初始化,基本学习率设置为0.0001. 整个训练epochs设定为70. 最后,用6个去噪块和5个多尺度卷积构成整个去噪网络。
[19] Delving deep into rectifiers: Surpassing human-level performance on imagenet classification
对比:LRTA,BM4D,LRTV,LRMR,NMoG和HSID-CNN
我们的网络将用5、25、50、75、100的固定噪声水平的高斯噪声进行训练。
指标:PSNR、SSIM、SAM
不同方法在华盛顿DC购物中心的比较结果如表1所示。图3显示了帕维亚中心数据集中所有方法的实验结果。表2证明了我们提出的方法中不同模块的有效性。图4显示了通过所有相关方法去噪的印度松的恢复结果。采用支持向量机(SVM)对恢复图像进行分类。表3所示分类结果。
代码
https://github.com/NWPUHWM/ENCAM
ADRN: Attention-based Deep Residual Network for Hyperspectral Image Denoising-对比上文的通道注意力块
引言
BM4D、LRTA、LRMR、LLRT、NG-Meet等,上述方法的主要缺点是,由于复杂的优化过程,它们非常耗时,这妨碍了它们在实践中的使用。另外,这些人工引入的先验知识只反映了数据某一方面的特征,因此这些方法的表示能力是有限的。
HSID-CNN、SSGN等,虽然这些方法取得了令人印象深刻的去噪效果,但仍有很大的潜力去探索和推广这一领域。
通道注意力机制被用来使网络集中于最有利于去噪过程的最相关的辅助信息和特征。为了提高判别学习的能力,我们将通道注意力机制集成到网络中,使其更好地意识到更相关的信息和更关键的特征。
方法
特征提取块:采用了感受野(reception field)大小为1、3、5、7的四种卷积层来提取空间和光谱特征。此外,为了避免昂贵的计算负担和加快测试速度,当滤波器尺寸大于1时,插入1×1卷积层以减小通道维数。
残差块:更深层次的网络往往存在梯度消失问题,使得训练过程缓慢甚至发散。为了解决这些问题,采用跳跃连接(shortcut connection),这大大增加了信息流,因此有助于预测残差噪声和梯度的反向传播,从而加速训练过程。
通道注意力块:从光谱输入中提取的特征映射对最终去噪结果的贡献不同,其中一些可能没有那么有益。因此,我们的网络学习应该集中在重要的特征上。此外,在残差学习策略中,负责高频(high-frequency)提取的卷积核应该得到更多的关注,以便于预测噪声。考虑到这些问题,我们引入了一个通道注意力块来自适应地调整特征表示。
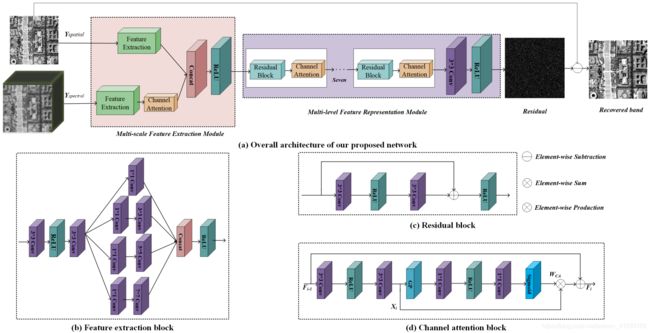
对于第 i i i个CAB,有 F i = F i − 1 + W C A ∗ X i F_{i}=F_{i-1}+W_{C A} * X_{i} Fi=Fi−1+WCA∗Xi其中 F i − 1 , F i F_{i-1},F_i Fi−1,Fi为输入、输出的特征映射, X i X_i Xi为由两个3×3的堆叠卷积层获得的残差分量(residual component) X i = W 2 ∗ δ ( W 1 ∗ F i − 1 ) X_{i}=W_{2} * \delta\left(W_{1} * F_{i-1}\right) Xi=W2∗δ(W1∗Fi−1)其中 W 1 , W 2 W_1,W_2 W1,W2为权重集, δ \delta δ为ReLU函数。

其中 W 3 , W 4 W_3,W_4 W3,W4为权重集,GP表示全局平均池化操作。
残差噪声: R = F ( Θ , Y spatial , Y spectral ) R=F\left(\Theta, Y_{\text {spatial}}, Y_{\text {spectral}}\right) R=F(Θ,Yspatial,Yspectral)
干净图像为: X ^ = Y spatial − R \hat{X}=Y_{\text {spatial}}-R X^=Yspatial−R
损失函数包括重建损失和正则化损失: L total = λ L rec + L reg L_{\text {total}}=\lambda L_{\text {rec}}+L_{\text {reg}} Ltotal=λLrec+Lreg, L r e c L_{rec} Lrec用于确保恢复的结果接近真实情况,而 L r e g L_{reg} Lreg用于确保残差噪声满足零均值分布:
L r e c = 1 N H W ∑ i = 1 N ∥ X ^ i − X i ∥ 2 2 L_{r e c}=\frac{1}{N H W} \sum_{i=1}^{N}\left\|\hat{X}^{i}-X^{i}\right\|_{2}^{2} Lrec=NHW1i=1∑N∥∥∥X^i−Xi∥∥∥22
L r e g = ( 1 N H W ∑ i = 1 N ∑ h = 1 H ∑ w = 1 W R h w i ) 2 L_{r e g}=\left(\frac{1}{N H W} \sum_{i=1}^{N} \sum_{h=1}^{H} \sum_{w=1}^{W} R_{h w}^{i}\right)^{2} Lreg=(NHW1i=1∑Nh=1∑Hw=1∑WRhwi)2
其中 N N N表示训练批次(batch)的数量, H H H和 W W W表示训练图像的高度和宽度。
训练细节:相邻波段数K=64,下采样比率r=10,折衷参数λ=10,我们使用截断正态分布(truncated normal distribution)来初始化权重,并从头(scratch)开始训练网络。使用Adam,mini-batch size = 382, β 1 = 0.9 \beta_1=0.9 β1=0.9, β 2 = 0.999 \beta_2=0.999 β2=0.999, ϵ = 1 e − 8 \epsilon=1 e-8 ϵ=1e−8,学习率从0.0001开始,每经过一定的训练步数(steps)(如5000)就呈指数衰减。总迭代次数大概在30万次左右。