剑指 Offer 12. 矩阵中的路径

题目描述

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

解题思路

方法一：深度优先搜索+剪枝

利用递归，从第一个元素开始，查询临近的四个方向上的元素是否符合要求，若第（i，j)个元素符合则检测该元素四个方向上的元素，不断延申，直到找到字符串或者返回没找到结束递归。

递归返回条件：

根据二维数组四个角的下标（0，0），（rows，0），（rows，cols），（0，cols），我们可以得到当横向边界小于0或者>=rows时，证明已经全部查询完毕；纵向边界<0或者>=cols，证明已经全部查询完毕，并且没有查询到字符串，返回false。（当二维数组有3列时，下标是0，1，2，因此当>=rows时表示已经越界了）

在匹配字符串时，每次匹配一个字符，当我们成功匹配字符串的最后一个时表示查找到了字符串，返回true。

然而在这种情况下会有一种情况，比如在下表中查找“ABCHHHD”：

A	B	C	D
M	A	H	D
D	E	H	F
U	D	H	I

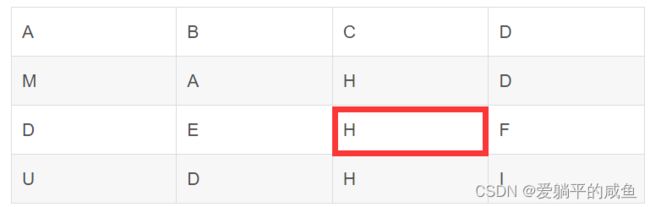
我们从A开始，到B，到C，到H，到H ，此时我们已经到达下面的位置：

 下一个要寻找的应该是下面的H，可是对于上述情况来说，如果代码中，向上寻找先于向下寻找，那么就会回到上面的H。因此我们需要在本次递归过程中标记已经访问过的元素。因此我们将访问过的并且成功匹配的字符更改内容为'\0'，退出本次递归时再还原回去。（因为其他的递归中可能并没有访问这个元素）

代码

class Solution
{
private:
	int rows;
	int cols;
	bool DFS(std::vector>& board, std::string word, int i, int j, int k)
    {
        if (i >= rows || i < 0 || j >= cols || j < 0 || board[i][j] != word[k])
                return false;
        if (k == word.size() - 1)
            return true;
        board[i][j] = '\0';
        bool res = DFS(board, word, i + 1, j, k + 1) ||
        DFS(board, word, i - 1, j, k + 1) ||
        DFS(board, word, i, j + 1, k + 1) ||        
        DFS(board, word, i, j - 1, k + 1);
        board[i][j] = word[k];
        return res;    
    }
public:
    bool Solution::exist(std::vector>& board, std::string word)
    {
        rows = board.size();
        cols = board[0].size();
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (DFS(board, word, i, j, 0)) return true;
            }
        }
        return false;
    }
};