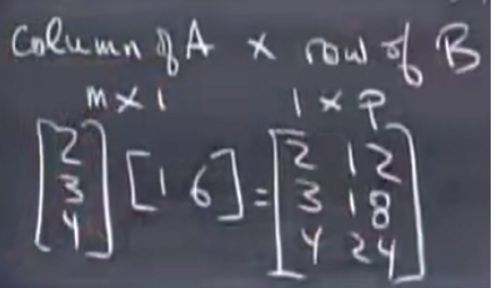MIT公开课18.06 Gilbert Strang 线性代数 笔记1 - Ax=b和四个子空间

相关链接

课程链接

B站

网易公开课

mit open course ware

线性代数的本质（简易版课程）：貌似有404的bug，b站搜索线性代数的本质即可

作业

参考笔记链接

github ApacheC 笔记书

CSDN 某博主笔记

问题

Win10视频单声道解决方案：
1.右键声音图标

2.打开声音设置

3.轻松访问音频设置

4.“打开单声道音频” 设为开

5.听完课后，可再设为关

第1讲：方程组的集合解释

1. 从方程组到矩阵

矩阵的诞生是为了用一种简洁的方式表达线性方程组
个人理解来说就是为了更好的描述和解决 Ax = b
从系统的角度来理解：
A：系统
x：输入
b：输出

2. $Ax=b$解法1：row picture 行图像

矩阵分为行row和列column
row picture 关注矩阵行部分

将行所代表的方程以直线形式画出，求出交点即可得到行图像，从而得到方程的解

三维时的解法：求出三个平面的交点

3. $Ax=b$解法2：column pircture 列图像

column picture关注列的部分，我们视一列为一个向量vector

求出合适的线性组合（linear combination），使得 Ax = b

数形结合：

数：

$$1\left[\begin{array}{c}2\\ -1\end{array}\right]+2\left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right](1)$$

A：等式左边的两个常数列向量拼接成的常矩阵
x：两个变量x,y组成的向量 (注意x的含义区分：前者为向量，后者为组成该向量的一个变量)
b：目标向量
x = 1，y = 2时，Ax = b

形：

1倍的列向量1 和 2倍的列向量2 进行矢量和，可得目标向量

三维时的解法：求出三个三维向量的线性组合，得到目标向量
（维度三维及以上时，列图像解法更具优势）

4.问题：于任意的b，是否都能求解$Ax=b$？用列向量线性组合的观点阐述就是，列三维情况下，向量的线性组合能否覆盖整个三维向量空间？

答：如果三个向量在同一个平面上，问题就出现了——他们的线性组合也一定都在这个平面上。举个例子，如果col3=col1 + col2 ，那么不管怎么组合，这三个向量的结果都逃不出这个平面，因此当b在平面内，方程组有解，而当b不在平面内，这三个列向量就无法构造出b。在后面的课程中，我们会了解到这种情形称为奇异、矩阵不可逆。

下面我们推广到九维空间，每个方程有九个未知数，共九个方程，此时已经无法从坐标图像中描述问题了，但是我们依然可以从求九维列向量线性组合的角度解决问题，仍然是上面的问题，是否总能得到bb？当然这仍取决于这九个向量，如果我们取一些并不相互独立的向量，则答案是否定的，比如取了九列但其实只相当于八列，有一列毫无贡献（这一列是前面列的某种线性组合），则会有一部分bb无法求得。

5. 矩阵乘法方法

5.1 向量内积

$$\begin{array}{l}A=\left[\begin{array}{lll}{a}_{1,1}& a_{1,2}& a_{1,3}\\ a_{2,1}& a_{2,2}& a_{2,3}\end{array}\right]\\ B=\left[\begin{array}{ll}{b}_{1,1}& b_{1,2}\\ b_{2,1}& b_{2,2}\\ b_{3,1}& b_{3,2}\end{array}\right]\\ C=AB=\left[\begin{array}{ll}{a}_{1,1}{b}_{1,1}+a_{1,2}{b}_{2,1}+a_{1,3}{b}_{3,1},& a_{1,1}{b}_{1,2}+a_{1,2}{b}_{2,2}+a_{1,3}{b}_{3,2}\\ a_{2,1}{b}_{1,1}+a_{2,2}{b}_{2,1}+a_{2,3}{b}_{3,1},& a_{2,1}{b}_{1,2}+a_{2,2}{b}_{2,2}+a_{2,3}{b}_{3,2}\end{array}\right]\end{array}$$
左矩阵的所有行向量与右矩阵的所有列向量分别相乘并求和

5.2 列向量的线性组合

$$\left[\begin{array}{cc}2& 5\\ 1& 3\end{array}\right]\left[\begin{array}{c}1\\ 2\end{array}\right]=1\left[\begin{array}{c}2\\ 1\end{array}\right]+2\left[\begin{array}{c}5\\ 3\end{array}\right]=\left[\begin{array}{c}12\\ 7\end{array}\right]$$
将Ax看作A各列的线性组合
教授更推荐此方法，当数据量较大时更有优势

第2讲：矩阵消元

1.高斯消元法

1.1消元步骤

对该方程消元：
$$\left[\begin{array}{lll}\underline{1}& 2& 1\\ 3& 8& 1\\ 0& 4& 1\end{array}\right]\stackrel{{\text{ row2-3row }}_1}{⟶}\left[\begin{array}{ccc}\underline{1}& 2& 1\\ 0& 2& -2\\ 0& 4& 1\end{array}\right]$$
2.以y为主元，在第三个方程中消去y项
$$\left[\begin{array}{ccc}\underline{1}& 2& 1\\ 0& \underline{2}& -2\\ 0& 4& 1\end{array}\right]\stackrel{\text{ row }3-2\mathrm{r}\mathrm{o}\mathrm{w}2}{⟶}\left[\begin{array}{ccc}\underline{1}& 2& 1\\ 0& \underline{2}& -2\\ 0& 0& \underline{5}\end{array}\right]$$
3.回代：

1.2 消元失效

主元不能为0，否则需要交换行，使主元不为0
若有一行全部为0，则消元失效，矩阵也不可逆

2.新视角看矩阵乘法

旧角度

以矩阵中的元素为基本单位
AB：第i行A的所有元素 与 第j列B的所有元素 对应相乘的和，为AB的第i行，第j列元素

新角度

以向量为基本单位

从列向量角度

该矩阵有三个列向量，分别乘以三个系数 3 4 5，再求和，得到一个 3×1 的列向量

从行向量角度

该矩阵有三个行向量，分别乘以三个系数 1 2 7， 再求和，得到一个 1×3 的行向量

3.以矩阵运算角度描述高斯消元

要求1：第二行减去 3倍的第一行，其余行都不变

步骤：
第一行，不变，所以是1倍的第一行
第二行，-3倍的第一行 + 1倍的第二行 + 0倍的第三行，得到行向量[0，2，-2]
第三行，不变，所以是1倍的第三行

这个消元矩阵记为$E_{21}$（E是指初等矩阵elementary matrix，由单位矩阵经过一次初等变换得到的矩阵；21是指使第2行，第1列元素为0）

要求2：第三行减去2倍的第二行，其余行不变
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HMR9iqOx-1597991355771)(./1597558951965.png)]

对于矩阵乘法，结合律有效：$E_{32}(E_{21}A)=(E_{32}{E}_{21})A=EA=U$这意味着问题变成了如何找到一个矩阵E 使得EA=U矩阵E就是一堆初等矩阵elementary matrix的积。

4. 置换矩阵

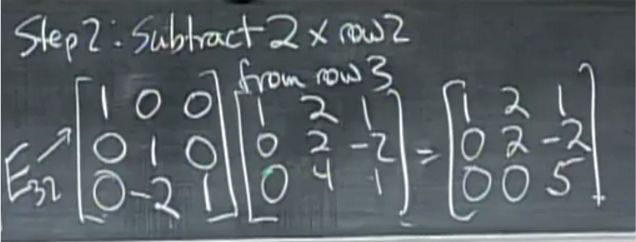
要对矩阵进行行变换：左乘一个矩阵
要对矩阵进行列变换：右乘一个矩阵

5.矩阵的逆

引申：我要如何才能由U变回A呢？由此引入矩阵的逆，即我们知道EA=U，那么有矩阵S使得SU=A，矩阵S即为矩阵E的逆。

第3讲：乘法和逆矩阵

1.矩阵乘法

矩阵能相乘的条件： 左矩阵的列数 = 右矩阵的行数（m×n和n×p）

1.1 一般性法则

$$c_{ij}=ro{w}_i\cdot colum{n}_j=\sum _{k=i}^n{a}_{ik}{b}_{kj}$$

1.2 整列相乘

1. B可以看作多个列向量
2. C中的第一列是A中的所有列的线性组合
3. B的第一列告诉我们是怎样的一个线性组合

1.3 整行相乘

1. A可以看作多个行向量
2. C中的第一行是B中的所有行的线性组合
3. A的第一行告诉我们是怎样的一个线性组合

1.4 列乘以行

定义：A的列 × B的行

C的每一行都是B的倍数，和B是同一方向，这是行空间（即行所有可能的线性组合，在此处是指[1,6]这条直线，C的所有行都在此直线上）
C的每一列都是A的倍数，和A是同一方向，这是列空间（即列所有可能的线性组合，在此处是指[2,3,4]这条直线，C的所有列都在此直线上）

矩阵形式：A的列分别乘以B的行，并求和

1.5 分块乘法

$$\left[\begin{array}{cc}{A}_1& A_2\\ A_3& A_4\end{array}\right]\left[\begin{array}{cc}{B}_1& B_2\\ B_3& B_4\end{array}\right]=\left[\begin{array}{cc}{A}_1{B}_1+A_2{B}_3& A_1{B}_2+A_2{B}_4\\ A_3{B}_1+A_4{B}_3& A_3{B}_2+A_4{B}_4\end{array}\right]$$

2.逆（方阵）

若存在逆，对于方阵，左逆右逆是相等的，非方阵则不等

矩阵存在逆：可逆的，非奇异的

矩阵不存在逆：不可逆的，奇异的

2.1证明不可逆

方法一：线性组合
若存在B，使A×B = I，因为结果I中的每一列都是A中的每一列的线性组合，且这两列共线，所以不可能得到单位矩阵的第一列[1,0]
方法二：存在非零向量x，使Ax=0

证明：如果对于非零的$x$仍有$Ax=0$，而$A$有逆$A^{-1}$，则$A^{-1}Ax=0$，即$x=0$，与题设矛盾，得证。

2.2若矩阵有逆，求逆的方法（高斯·若尔丹Gauss-Jordan法）

求逆实质上就是解方程

分解成两个方程
Gauss-jordan：同时求解多个方程

• 构造这样一个矩阵$\left[\begin{array}{cccc}1& 3& 1& 0\\ 2& 7& 0& 1\end{array}\right]$，接下来用消元法将左侧变为单位矩阵；
• $\left[\begin{array}{cccc}1& 3& 1& 0\\ 2& 7& 0& 1\end{array}\right]\stackrel{ro{w}_2-2ro{w}_1}{}\left[\begin{array}{cccc}1& 3& 1& 0\\ 0& 1& -2& 1\end{array}\right]\stackrel{ro{w}_1-3ro{w}_2}{}\left[\begin{array}{cccc}1& 0& 7& -3\\ 0& 1& -2& 1\end{array}\right]$
• 于是，我们就将矩阵从$\left[\begin{array}{cc}A& I\end{array}\right]$变为$\left[\begin{array}{cc}I& A^{-1}\end{array}\right]$

证明：高斯-若尔当法的本质是使用消元矩阵$E$，对$A$进行操作，$E\left[\begin{array}{cc}A& I\end{array}\right]$，利用一步步消元有$EA=I$，进而得到$\left[\begin{array}{cc}I& E\end{array}\right]$，其实这个消元矩阵$E$就是$A^{-1}$，而高斯-若尔当法中的$I$只是负责记录消元的每一步操作，待消元完成，逆矩阵就自然出现了。

第4讲：$A$的$LU$分解

矩阵的逆和转置

为什么逆矩阵要反过来？这就像是…你先把鞋子脱了再脱袜子，那么反过来不就是要先穿上袜子，再穿鞋子吗？所以说，忘记书上的蠢例子吧。

$AB$的逆矩阵：
$$\begin{gathered} \begin{array}{rl}A\cdot A^{-1}=I& =A^{-1}\cdot A\\ (AB)\cdot (B^{-1}{A}^{-1})& =I\\ \text{则}AB\text{的逆矩阵为}& B^{-1}{A}^{-1}\end{array} \\ \text{转置也如此} \end{gathered}$$

$A^T$的逆矩阵：
$$\begin{gathered} \begin{array}{rl}(A\cdot A^{-1}{)}^T& =I^T\\ (A^{-1}{)}^T\cdot A^T& =I\\ \text{则}{A}^T\text{的逆矩阵为}& (A^{-1}{)}^T\end{array} \\ \text{矩阵的逆符号和转置符号可随意切换} \end{gathered}$$

$LU$分解

其实，消元的目的只是为了正确认识矩阵的概念，而LU分解是最基础的矩阵分解。

前提：无主元为0的情况，即没有行交换
L： lower triangular matrix下三角矩阵
U：upper triangular matrix上三角矩阵

将一个 $n$ 阶方阵 $A$ 变换为 $U$ 需要的计算量估计：

我们需要运算（将一行乘一定倍数后加到另一行上消元，每一个元素进行这样的过程计为 一次运算）多少次之后，才能将其化为上三 角矩阵 U 呢？

1. 第一步，将$a_{11}$作为主元，需要的运算量约为$n^2$
   $$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]消元\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ 0& a_{22}& \cdots & a_{2n}\\ 0& ⋮& \ddots & ⋮\\ 0& a_{n2}& \cdots & a_{nn}\end{array}\right]$$

2. 以此类推，第二步变为99×99的矩阵，接下来每一步计算量约为$(n-1{)}^2、(n-2{)}^2、\cdots 、2^2、1^2$。

3. 则将 $A$ 变换为 $LU$ 的总运算量应为$O(n^2+(n-1{)}^2+\cdots +2^2+1^2)$，通过微积分的知识可知大约为$O(\frac{n^3}{3})$。

置换矩阵(Permutation Matrix)：

当主元等于0时，我们需要交换行来选择新的主元，用于交换行的矩阵称为置换矩阵

3阶方阵的置换矩阵有6个：
$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]$$
第五个矩阵和第六个矩阵互逆
其余矩阵都跟自己互逆
可以发现置换矩阵的运算构成一个群

置换矩阵的逆 = 置换矩阵的转置

第5讲：转置-置换-向量空间$R$

置换矩阵（Permutation Matrix）

置换矩阵：行重新排列了的单位矩阵

若A可逆，LU分解中若主元都不为0则我们无需进行行互换，当主元存在0时，我们需要将其与一个合适的行互换来继续LU分解，最后我们会得到

$PA=LU$

$n$阶方阵的置换矩阵P有$\left(\genfrac{}{}{0ex}{}{n}{1}\right)=n!$个。（全排列）

对置换矩阵$P$，有$P^{T}P=I$

即$P^T=P^{-1}$

转置矩阵（Transpose Matrix）

$(A^T{)}_{ij}=(A{)}_{ji}$

对称矩阵（Symmetric Matrix）

$A^T$ = $A$

证明：对任意矩阵$R$有$R^{T}R$为对称矩阵：

$$\begin{gathered} (R^{T}R{)}^T=(R{)}^T(R^T{)}^T=R^{T}R \\ \text{即}(R^{T}R{)}^T=R^{T}R \end{gathered}$$

向量空间（Vector Space）

向量空间定义：向量空间中任意向量满足加法和数乘封闭（线性组合）

所有向量空间都必须包含原点（Origin），因为 0 数乘 一个向量 = 零向量

向量子空间

向量空间的子集组成的向量空间

在$R^2$中的向量子空间只能是：
①$R^2$本身
②一条线（过零点）
③零向量单独组成的空间

在$R^3$中的向量子空间只能是：
①$R^3$本身
②一条线（过零点）
③一个平面（过零点）
④零向量单独组成的空间

$R^n$类推

列空间

让我们以向量空间的方式来观察矩阵，对于矩阵A

取出$A$的两个列向量，其线性组合即构成了一个向量空间，我们称之为列空间，很明显这是一个在$R^3$内的平面

第6讲：列空间和零空间

对向量空间$S$和$T$，有：
1.$S\cap T$也是向量空间
证明：
对属于$S\cap T$的向量$x$，他们的线性组合满足$S$的运算封闭和$T$的运算封闭，故其线性组合得到的向量也在$S\cap T$内

2.$S\cup T$不一定是向量空间

列空间

回忆第二课关于矩阵乘法的内容,$Ax$相乘，$A$为矩阵，$x$为向量，二者相乘的结果可以看做是$A$中列向量的线性组合

由$A$的列向量线性组合生成的子空间为$A$的列空间

$Ax=b$有解当且仅当$b$属于$A$的列空间

零空间

$A$的零空间是$Ax=0$中$x$的解组成的集合。

零空间是一个向量空间，证明：
设$x_1$,$x_2$在零空间中，
1.$A(x_1+x_2)=A{x}_1+A{x}_2=0$，满足
2.$A(k{x}_1)=kA{x}_1=0$，对$x_2$同理，满足

对于$Ax=b,b\ne 0$的情况，都不是向量空间，因为都不过零点

以上两种子空间的总结：有两种方法构造子空间，
其一是通过A的列向量的线性组合构造列空间，
其二是求解向量必须满足的方程组来构造子空间（通过让$x$满足特定条件来得到子空间，$Ax=0$将构造出零空间）

第7讲：求解$Ax=0$ 主变量 特解

行阶梯矩阵

举例：$3\times 4$矩阵
$$A=\left[\begin{array}{cccc}1& 2& 2& 2\\ 2& 4& 6& 8\\ 3& 6& 8& 10\end{array}\right]$$，求$Ax=0$的特解：

找出主变量（pivot variable）：
$$A=\left[\begin{array}{cccc}1& 2& 2& 2\\ 2& 4& 6& 8\\ 3& 6& 8& 10\end{array}\right]消元\left[\begin{array}{cccc}\underline{1}& 2& 2& 2\\ 0& 0& \underline{2}& 4\\ 0& 0& 0& 0\end{array}\right]=U$$

主变量（pivot variable，下划线元素）的个数为2，即矩阵$A$的秩（rank）为2，即$r=2$。

主变量所在的列为主列（pivot column），其余列为自由列（free column）。

自由列中的变量为自由变量（free variable），自由变量的个数为$n-r=4-2=2$。

通常，给自由列变量赋值，去求主列变量的值。如，令$x_2=1,x_4=0$求得特解
$x=c_1\left[\begin{array}{c}-2\\ 1\\ 0\\ 0\end{array}\right]$；
再令$x_2=0,x_4=1$求得特解
$x=c_2\left[\begin{array}{c}2\\ 0\\ -2\\ 1\end{array}\right]$。

简化行阶梯矩阵

该例还能进一步简化，即 将$U$矩阵化简为$R$矩阵（Reduced row echelon form），即简化行阶梯形式。

在简化行阶梯形式中，主元为1，主元上下的元素都是$0$：
$$U=\left[\begin{array}{cccc}\underline{1}& 2& 2& 2\\ 0& 0& \underline{2}& 4\\ 0& 0& 0& 0\end{array}\right]化简\left[\begin{array}{cccc}\underline{1}& 2& 0& -2\\ 0& 0& \underline{1}& 2\\ 0& 0& 0& 0\end{array}\right]=R$$

将$R$矩阵中的主变量放在一起，自由变量放在一起（列交换），得到

$$R=\left[\begin{array}{cccc}\underline{1}& 2& 0& -2\\ 0& 0& \underline{1}& 2\\ 0& 0& 0& 0\end{array}\right]列交换\left[\begin{array}{cccc}1& 0& 2& -2\\ 0& 1& 0& 2\\ 0& 0& 0& 0\end{array}\right]=\left[\begin{array}{cc}I& F\\ 0& 0\end{array}\right]\text{，其中}I\text{为单位矩阵，}F\text{为自由变量组成的矩阵}$$

什么样的$x$满足$Rx=0$ ？
计算零空间矩阵$N$（null space matrix），其各列为特解，有$RN=0$。

$$\begin{gathered} x_{pivot}=-F{x}_{free} \\ \left[\begin{array}{cc}I& F\end{array}\right]\left[\begin{array}{c}{x}_{pivot}\\ x_{free}\end{array}\right]=0 \\ N=\left[\begin{array}{c}-F\\ I\end{array}\right] \end{gathered}$$

在本例中
$N=\left[\begin{array}{cc}-2& 2\\ 0& -2\\ 1& 0\\ 0& 1\end{array}\right]$，与上面求得的两个$x$特解一致。

另一个例子，矩阵转置后
$A=\left[\begin{array}{ccc}1& 2& 3\\ 2& 4& 6\\ 2& 6& 8\\ 2& 8& 10\end{array}\right]消元\left[\begin{array}{ccc}1& 2& 3\\ 0& 2& 2\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]化简\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]=R$

矩阵主列的个数与其转置相同，所以矩阵的秩仍为$r=2$，有$2$个主变量，$1$个自由变量。

同上一例，取自由变量为$x_3=1$，求得特解
$x=c\left[\begin{array}{c}-1\\ -1\\ 1\end{array}\right]$

第8讲：求解$Ax=b$可解性和解的结构

$b$是什么时，$Ax=b$有解？

$b$在$A$的列空间内，即$b$必须是$A$各列的线性组合
或者说，如果$A$各行的线性组合得到零行，$b$端分量的同样组合也必须为0

求解$Ax=b$算法

①求特解：
将所有自由变量设为0
求解出主元变量
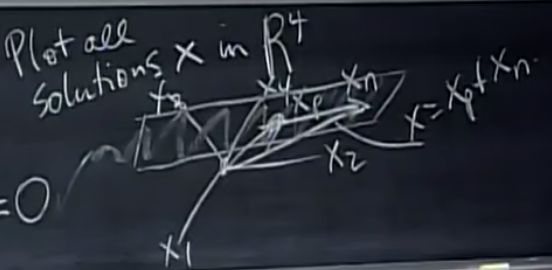
②加上零空间的任意$x$

对于方程组某解，其与零空间内任意向量之和仍为解：
$$A(X_p+X_n)=b$$
举例，同上一讲：$3\times 4$矩阵
$A=\left[\begin{array}{cccc}1& 2& 2& 2\\ 2& 4& 6& 8\\ 3& 6& 8& 10\end{array}\right]$，求$Ax=b$的特解：

写出其增广矩阵（augmented matrix）$\left[\begin{array}{cc}A& b\end{array}\right]$：

$$\left[\begin{array}{ccccc}1& 2& 2& 2& b_1\\ 2& 4& 6& 8& b_2\\ 3& 6& 8& 10& b_3\end{array}\right]消元\left[\begin{array}{ccccc}1& 2& 2& 2& b_1\\ 0& 0& 2& 4& b_2-2b_1\\ 0& 0& 0& 0& b_3-b_2-b_1\end{array}\right]$$

有解的必要条件为$b_3-b_2-b_1=0$。

假设$b=\left[\begin{array}{c}1\\ 5\\ 6\end{array}\right]$

解法：令所有自由变量取$0$,求得特解
$x_p=\left[\begin{array}{c}-2\\ 0\\ \frac{3}{2}\\ 0\end{array}\right]$。

$Ax=b$的解集为其特解加上零空间，对本例有：
$x_{complete}=\left[\begin{array}{c}-2\\ 0\\ \frac{3}{2}\\ 0\end{array}\right]+c_1\left[\begin{array}{c}-2\\ 1\\ 0\\ 0\end{array}\right]+c_2\left[\begin{array}{c}2\\ 0\\ -2\\ 1\end{array}\right]$

图像大致如此，为四维空间中一不过原点的平面：

对秩为$r$的$m\times n$矩阵$A$的解讨论

对于$m\times n$矩阵$A$，有矩阵$A$的秩$r\le min(m,n)$

①列满秩$r=n$情况：
每一列都有主元
$rank(A)=2$，没有自由变量，所以零空间中只有零向量
全体解 = 特解 + 零空间
$b$取$A$中各列的线性组合才有解，并且这个解唯一
所以要么有0个解，要么1个解
$$A=\left[\begin{array}{cc}1& 3\\ 2& 1\\ 6& 1\\ 5& 1\end{array}\right]$$
该例中，若b = $\left[\begin{array}{c}4\\ 3\\ 7\\ 6\end{array}\right]$
则有唯一解，$x=\left[\begin{array}{c}1\\ 1\end{array}\right]$

②行满秩$r=m$情况：
每一行都有主元，没有零行
$$A=\left[\begin{array}{cccc}1& 2& 6& 5\\ 3& 1& 1& 1\end{array}\right]$$
$rank(A)=2$，$\forall b\in R^m都有x\ne 0的解$，因为此时$A$的列空间为$R^m$，$b\in R^m$恒成立，假如r0，组成$A$的零空间的自由变量有n-r个，则有无穷多的解

③行列满秩情况：$r=m=n$
是一可逆方阵
如，
$$A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$$
则$A$最终可以化简为$R=I$，其零空间只包含$0$向量。
同时包含行满秩和列满秩的特点，即无论$b$为何值，都有解，且这个解唯一

④一般情况：$r<m,r<n$
b分量可能不符合0=0,则有0个解
否则，n-r>0，组成$A$的零空间的自由变量有n-r个，有无穷多的解
总结：

$$\begin{array}{cccc}r=m=n& r=n<m& r=m<n& r<m,r<n\\ R=I& R=\left[\begin{array}{c}I\\ 0\end{array}\right]& R=\left[\begin{array}{cc}I& F\end{array}\right]& R=\left[\begin{array}{cc}I& F\\ 0& 0\end{array}\right]\\ 1solution& 0or1solution& \infty solution& 0or\infty solution\end{array}$$

第9讲：线性相关性、基、维数

线性相关性

前言知识：

$m<n$，即未知数$x$的个数 > 方程的个数时，
零空间不止包含零向量，存在自由变量
存在$Ax=0$的非零解

结论：
当向量（向量组）$v_1,v_2,v_3...v_n$是矩阵$A$的列向量，
① 他们是线性无关的，当且仅当：
零空间角度：$A$的零空间只有零
秩的角度：$r=n$（无自由变量）

② 他们是线性相关的，当且仅当：
零空间角度：$A$的零空间除零向量外还存在其他向量
秩的角度：$r<n$，（存在自由变量）

基

生成：指一些向量的所有线性组合

向量空间$S$中的一组基（basis），具有两个性质：

1. 他们线性无关；
2. 他们可以生成$S$。

对于向量空间${\mathbb{R}}^n$，如果$n$个向量组成的矩阵为可逆矩阵，则这$n$个向量为该空间的一组基。

对于给定一空间，基向量个数相等

维数

对于给定一空间，其基向量个数被称为维数（dimension）
举例：
$$A=\left[\begin{array}{cccc}1& 2& 3& 1\\ 1& 1& 2& 1\\ 1& 2& 3& 1\end{array}\right]$$
A的列向量线性相关，其零空间中有非零向量
$2=rank(A)=主列的个数=列空间维数$

可以很容易的求得$Ax=0$的两个解，如
$$x_1=\left[\begin{array}{c}-1\\ -1\\ 1\\ 0\end{array}\right],x_2=\left[\begin{array}{c}-1\\ 0\\ 0\\ 1\end{array}\right]$$
$n-rank(A)=2=自由变量存在的列数=零空间维数$

我们得到：列空间维数$dimC(A)=rank(A)$，零空间维数$dimN(A)=n-rank(A)$

第10讲：四个基本子空间

子空间	记号	属于	维数	基
列空间	$C(A)$	${\mathbb{R}}^m$	r	所有主列
零空间	$N(A)$	${\mathbb{R}}^n$	n-r	所有特殊解(这里不是指特解，而是一般解，特解叫特定解)
行空间	$C(A^T)$	${\mathbb{R}}^n$	r	行最简形的前r行，详见例1
左零空间	$N(A^T)$	${\mathbb{R}}^m$	m-r	用E记录把$A$化作$R$的过程，R为零行所对应的E即为基，详见例2

列空间（$C(A)$）

列向量的所有线性组合组成的空间

零空间（$N(A)$）

自由元所在的列即可组成零空间的一组基。

行空间（$C(A^T)$）

行的所有组合组成的空间，也可以看作$A^T$的列空间

左零空间（$N(A^T)$）

对于左零空间，有$A^{T}y=0\to (A^{T}y{)}^T=0^T\to y^{T}A=0^T$，因此得名。

例子

例1，对于行空间
$$A=\left[\begin{array}{cccc}1& 2& 3& 1\\ 1& 1& 2& 1\\ 1& 2& 3& 1\end{array}\right]消元、化简\left[\begin{array}{cccc}1& 0& 1& 1\\ 0& 1& 1& 0\\ 0& 0& 0& 0\end{array}\right]=R$$

由于我们做了行变换，本质是行向量进行线性组合，A的列空间受到影响，$C(R)\ne C(A)$，而行变换并不影响行空间，所以可以在$R$中看出前两行就是行空间的一组基。

所以，可以得出无论对于矩阵$A$还是$R$，其行空间的一组基，可以由$R$矩阵的前$r$行向量组成（这里的$R$就是第七讲提到的简化行阶梯形式）。

例2，对于左零空间，有$A^{T}y=0\to (A^{T}y{)}^T=0^T\to y^{T}A=0^T$，因此得名。

采用Gauss-Jordan消元，将增广矩阵$\left[\begin{array}{cc}{A}_{m\times n}& I_{m\times m}\end{array}\right]$中$A$的部分划为简化行阶梯形式$\left[\begin{array}{cc}{R}_{m\times n}& E_{m\times m}\end{array}\right]$，此时矩阵$E$会将所有的行变换记录下来。

则$EA=R$，而在前几讲中，有当$A^{\prime }$是$m$阶可逆方阵时，$R^{\prime }$即是$I$，所以$E$就是$A^{-1}$。

本例中

$$\left[\begin{array}{cc}{A}_{m\times n}& I_{m\times m}\end{array}\right]=\left[\begin{array}{ccccccc}1& 2& 3& 1& 1& 0& 0\\ 1& 1& 2& 1& 0& 1& 0\\ 1& 2& 3& 1& 0& 0& 1\end{array}\right]消元、化简\left[\begin{array}{ccccccc}1& 0& 1& 1& -1& 2& 0\\ 0& 1& 1& 0& 1& -1& 0\\ 0& 0& 0& 0& -1& 0& 1\end{array}\right]=\left[\begin{array}{cc}{R}_{m\times n}& E_{m\times m}\end{array}\right]$$

则

$$EA=\left[\begin{array}{ccc}-1& 2& 0\\ 1& -1& 0\\ -1& 0& 1\end{array}\right]\cdot \left[\begin{array}{cccc}1& 2& 3& 1\\ 1& 1& 2& 1\\ 1& 2& 3& 1\end{array}\right]=\left[\begin{array}{cccc}1& 0& 1& 1\\ 0& 1& 1& 0\\ 0& 0& 0& 0\end{array}\right]=R$$

很明显，式中$E$的最后一行对$A$的行做线性组合后，得到$R$的最后一行，即$0$向量，也就是$y^{T}A=0^T$。

矩阵空间

最后，引入矩阵空间的概念，矩阵可以同向量一样，做求和、数乘。
矩阵也满足向量空间的八大运算律

就像把$R^n$延伸到$R^{n\times n}$

举例，设所有$3\times 3$矩阵组成的矩阵空间为$M$。则上三角矩阵、对称矩阵、对角矩阵（前两者的交集）是其子空间。

观察一下对角矩阵，如果取
$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& 3& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 7\end{array}\right]$$
可以发现，任何三阶对角矩阵均可用这三个矩阵的线性组合生成，因此，他们生成了三阶对角矩阵空间，即这三个矩阵是三阶对角矩阵空间的一组基。

第11讲：矩阵空间、秩1矩阵和小世界图

矩阵空间

不要在意矩阵与矩阵之间的乘法，仅考虑矩阵加法和数乘

使用$3\times 3$矩阵举例，其矩阵空间记为$M$。

则$M$的一组基为：
$$\begin{gathered} \left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 1\\ 0& 0& 0\\ 0& 0& 0\end{array}\right] \\ \left[\begin{array}{ccc}0& 0& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right] \\ \left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 1& 0\end{array}\right]\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right] \end{gathered}$$

易得，$dimM=9$。

一些子空间

对称矩阵S （symmetric）

对于对称矩阵，由于其对角线有三个线性无关元素，左上角的三个元素与右下角三个元素有线性关系，其维度dimension为6

上三角矩阵U （upper triangular）

对角线以下全为0，对角线以上6个元素可以线性无关，维度dimension为6。

矩阵空间的交与和

对于对称矩阵空间$S$和上三角矩阵空间$U$，其交集$S\cap U$为对角矩阵，维数是3

$S+U$指，属于$S$的任一矩阵与属于$U$的任一矩阵的和

$S\cup U$并不构成子空间，相对于$S\cup U$，我们对$S+U$更感兴趣
因为$S\cup U$只是简单地把$S$和$U$放在了一起，而我们更感兴趣的$S+U$，它不仅包括放在一起的部分，还包$S$和$U$拓展的部分，其维数为9

已知：
$$\begin{gathered} dim(S)=6，dim(U)=6 \\ dim(S\cap U)=3，dim(S+U)=9 \\ 6+6=3+9 \end{gathered}$$
引出性质：
$$dim(S)+dim(U)=dim(S\cap U)+dim(S+U)$$

微分方程例子

线性代数，基，维度等概念，不局限于向量和矩阵
函数也可以看作是向量，因为可以对他们做加法，数乘，线性组合

$\frac{d^{2}y}{d{x}^2}+y=0$，即$y^{\prime \prime }+y=0$

求这个方程的解就是在找$Ax=0$一个零空间

方程的解有：$y=\cos x,y=\sin x,y=e^{ix},y=e^{-ix}$等等（$e^{ix}=\cos x+i\sin x,e^{-ix}=\cos x-i\sin x$）

而该方程的所有解：$y=c_1\cos x+c_2\sin x$。

所以，该方程的零空间（即解空间）的一组基为$\cos x,\sin x$，零空间的维数为$2$。同理$e^{ix},e^{-ix}$可以作为另一组基。

秩1矩阵

秩1矩阵的分解

秩1矩阵分解为主列和主行向量

$2\times 3$矩阵$A=\left[\begin{array}{ccc}1& 4& 5\\ 2& 8& 10\end{array}\right]=\left[\begin{array}{c}1\\ 2\end{array}\right]\left[\begin{array}{ccc}1& 4& 5\end{array}\right]$。

且$dimC(A)=1=dimC(A^T)$，所有的秩一矩阵都可以划为$A=U{V}^T$的形式，这里的$U,V$均为列向量。

秩一矩阵类似“积木”，可以搭建任何矩阵，如对于一个$5\times 17$秩为$4$的矩阵，只需要$4$个秩一矩阵就可以组合出来。

问题1：所有的秩4的$5\times 17$矩阵能构成一个子空间吗

令$M$代表所有$5\times 17$，$M$中所有秩$4$矩阵组成的集合并不是一个子空间
$一般来说，两个矩阵之和的秩\le 两个矩阵的秩之和$
两个秩$4$矩阵相加，其结果并不一定是秩四矩阵。

同理，两个秩1矩阵相加，其结果不一定是秩1矩阵，可能会是秩2矩阵。于是就有了矩阵分解成秩1矩阵的可能性。

问题2：取${\mathbb{R}}^4$中满足$v_1+v_2+v_3+v_4=0$的所有向量。能组成一个向量子空间吗？

现在，在${\mathbb{R}}^4$空间中有向量$v=\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]$，取${\mathbb{R}}^4$中满足$v_1+v_2+v_3+v_4=0$的所有向量组成一个向量空间$S$
则$S$是一个向量子空间。

证明：

易看出，不论是使用系数乘以该向量，或是用两个满足条件的向量相加，其结果仍然满足$v_1+v_2+v_3+v_4=0$，落在分量和为零的向量空间中。

求子空间$S$

求$S$的维数：

从另一个角度看，$v_1+v_2+v_3+v_4=0$等价于$\left[\begin{array}{cccc}1& 1& 1& 1\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]=0$，则$S$就是$A=\left[\begin{array}{cccc}1& 1& 1& 1\end{array}\right]$的零空间。

$rank(A)=1$，则对其零空间有$rank(N(A))=n-r=3=dimN(A)$，则$S$的维数是$3$。

顺便看一下$1\times 4$矩阵$A$的四个基本子空间：

行空间：$dimC(A^T)=1$，其中的一组基是 [ 1 1 1 1 ] \begin{bmatrix}1\\1\\1\\1\end{bmatrix} ⎣⎢⎢⎡​