蓄水池抽样算法(reservoir sampling)
蓄水池抽样算法(reservoir sampling)
场景:在长度未知的数据流中,等概率地采样一定数量的数据。即,数据量N未知,若要求采样k个数据,采样概率保证 k N \frac{k}{N} Nk。
要求:只遍历一遍数据,空间复杂度: O ( N ) O(N) O(N)。
内容提要:算法主要思想、证明、LeetCode真题、Java源码。
文章目录
- 蓄水池抽样算法(reservoir sampling)
-
- 证明
-
- K=1时
- K>1时
- K>1时,蓄水池抽样算法JAVA完整版
- k=0时,蓄水池抽样算法JAVA完整版
- LeetCode原题
-
- [398. 随机数索引](https://leetcode-cn.com/problems/random-pick-index/)
- [382. 链表随机节点](https://leetcode-cn.com/problems/linked-list-random-node/)
- 埋个坑:分布式蓄水池抽样算法
- 埋个坑2:
1、申请一个长度为K的数组A保存抽样,数组A相当于容量为K的蓄水池。
2、保存首先接收到的K个元素
3、当接收到第i个新元素t时,以k/i的概率随机替换A中的元素(即生成[1,i]间随机数j,若j<=k,则以t替换A[j])
Init : a reservoir with the size: k
for i= k+1 to N
M=random(1, i);
if( M < k) // 要保证是以k/i的概率随机替换A中的元素
SWAP the Mth value and ith value
end for
证明
K=1时
数据流: x 1 , x 2 , ⋯ , x i , x i + 1 , ⋯ , x N − 1 , x N x_1, x_2, \cdots, x_i, x_{i+1}, \cdots, x_{N-1}, x_N x1,x2,⋯,xi,xi+1,⋯,xN−1,xN
K=1时,相当于要在N个数据流中选择一个数据,此时假设数据的增长下标为i,i从1开始,当i=1时,随机选择一个数据的概率P为1;当i=2时,P为1/2;当i=3时,P为1/3。并且,不论i等于几,第一个数取到的概率总是 1 i \frac{1}{i} i1。当这个过过程结束时,每一个对象都有相同的被选概率 1 n \frac{1}{n} n1。
证明:
第 i i i个被选中概率=选择第 i i i个对象的概率 × \times ×第 i i i个对象到第 n n n个对象没有被选择的概率
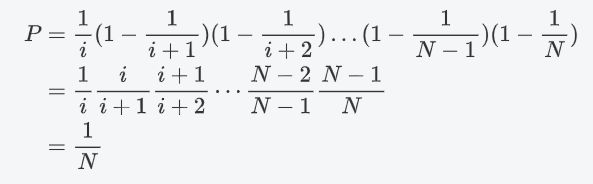
K>1时
数据流: x 1 , x 2 , ⋯ , x i , x i + 1 , ⋯ , x N − 1 , x N x_1, x_2, \cdots, x_i, x_{i+1}, \cdots, x_{N-1}, x_N x1,x2,⋯,xi,xi+1,⋯,xN−1,xN
蓄水池: x 1 , x 2 , ⋯ , x i , x i + 1 , ⋯ , x K − 1 , x K x_1, x_2, \cdots, x_i, x_{i+1}, \cdots, x_{K-1}, x_K x1,x2,⋯,xi,xi+1,⋯,xK−1,xK
问题就转化为,保证数据出现在蓄水池中的概率为 K N \frac{K}{N} NK。
当K大于1时,要在N个数据流中选择K个数据,保证每一个数据被选择的概率相同: K N \frac{K}{N} NK。
-
第一种情况:当N小于K时,取每一个对象的概率都相同,每一个都会被取到,所以为1;
-
第二种情况:当N大于K时,需要分步完成:
-
第1步,先将蓄水池装满:
-
第2步,当蓄水池装满之后,我们以第 i i i个对象 x i x_i xi为例,此时 i i i必然是大于K的
此时对于对象 x i x_i xi来说有两种情况:
-
第一种情况: x i x_i xi未被选中。
此时蓄水池中的元素不会被替换,此时蓄水池中的每一个元素出现的概率都是相同的,具体就是 x i x_i xi未被选中的概率 1 − K i 1-\frac{K}{i} 1−iK,可以理解为, x i x_i xi被选中概率为 K i \frac{K}{i} iK,未被选中的概率就是 1 − 被 选 中 的 概 率 1-被选中的概率 1−被选中的概率。
-
第二种情况: x i x_i xi被选中。这里也要分两种情况讨论。
- x i x_i xi被选中并且替换了蓄水池中的任意一个元素:此时, x i x_i xi被选中的概率为 K i \frac{K}{i} iK,蓄水池中有一个元素要被替换,蓄水池中的元素被替换的概率为 1 K \frac{1}{K} K1,那么蓄水池中的任意元素被 x i x_i xi替换的概率为 K i 1 K = 1 i \frac{K}{i} \frac{1}{K} = \frac{1}{i} iKK1=i1。
- x i x_i xi被选中但是没有替换蓄水池中的任意一个元素: K i ( 1 − 1 K ) = K − 1 i \frac{K}{i} (1 - \frac{1}{K}) = \frac{K-1}{i} iK(1−K1)=iK−1。
-
最后,总结以上的思路,回归我们最终的目的是求解 x i x_i xi被选中的概率P,可以有两种思路:
其实上述的两种分析只是从不同的概率角度来思考的,本质没有区别。
-
K>1时,蓄水池抽样算法JAVA完整版
public static int[] reservoirSampling(int[] nums, int k){
Random random = new Random();
// 定义一个蓄水池
int[] res = new int[k];
int len = nums.length;
for (int i = 0; i < len; i++) {
// 当数据流长度小于目标k值时,依次将k个数据加入蓄水池
if (i < k){
res[i] = nums[i];
continue;
}
// 当数据流长度大于k时,生成一个[0,i)的随机数
int r = random.nextInt(i);
// 根据上述算法分析过程要保证在i个数据中选中对象x_i的概率为k/i
// 就要限制 r < k
// 即可以理解为r在i个数据中选出k个数据的概率为k/i
if (r < k){
res[r] = nums[i];
}
}
return res;
}
k=0时,蓄水池抽样算法JAVA完整版
public static int reservoirSampling(int[] nums) {
Random random = new Random();
int len = nums.length;
int res = 0;
for (int i = 0; i < len; i++) {
int r = random.nextInt(i+1); // 注意random的取值是[0,i)
// 根据上述的算法分析,取到第1个元素的概率总是1/i
if (r == 0) {
res = nums[i];
}
}
return res;
}
LeetCode原题
398. 随机数索引
给定一个可能含有重复元素的整数数组,要求随机输出给定的数字的索引。 您可以假设给定的数字一定存在于数组中。
注意:
数组大小可能非常大。 使用太多额外空间的解决方案将不会通过测试。
示例:
int[] nums = new int[] {1,2,3,3,3};
Solution solution = new Solution(nums);
// pick(3) 应该返回索引 2,3 或者 4。每个索引的返回概率应该相等。
solution.pick(3);
// pick(1) 应该返回 0。因为只有nums[0]等于1。
solution.pick(1);
class Solution {
private int[] nums;
public Solution(int[] nums) {
this.nums = nums;
}
public int pick(int target) {
Random random = new Random();
int len = nums.length, res = 0, conut = 0;
for (int i = 0, count = 0; i < len; ++i) {
if (nums[i] == target) {
count++;
if (random.nextInt(count) == 0) {
res = i;
}
}
}
return res;
}
}
382. 链表随机节点
给你一个单链表,随机选择链表的一个节点,并返回相应的节点值。每个节点 被选中的概率一样 。
实现 Solution 类:
Solution(ListNode head) 使用整数数组初始化对象。
int getRandom() 从链表中随机选择一个节点并返回该节点的值。链表中所有节点被选中的概率相等。
示例:
输入
["Solution", "getRandom", "getRandom", "getRandom", "getRandom", "getRandom"]
[[[1, 2, 3]], [], [], [], [], []]
输出
[null, 1, 3, 2, 2, 3]
解释
Solution solution = new Solution([1, 2, 3]);
solution.getRandom(); // 返回 1
solution.getRandom(); // 返回 3
solution.getRandom(); // 返回 2
solution.getRandom(); // 返回 2
solution.getRandom(); // 返回 3
// getRandom() 方法应随机返回 1、2、3中的一个,每个元素被返回的概率相等。
class Solution {
ListNode head;
public Solution(ListNode head) {
this.head = head;
}
public int getRandom() {
Random random = new Random();
// 用一个变量来来存贮进入数据流的个数
int count = 1;
int res = 0;
ListNode cur = head;
while (cur != null){
if (random.nextInt(count) == 0){
res = cur.val;
}
cur = cur.next;
count++;
}
return res;
}
}
埋个坑:分布式蓄水池抽样算法
一块CPU的计算能力再强,也总有内存和磁盘IO拖他的后腿。因此为提高数据吞吐量,分布式的硬件搭配软件是现在的主流。
如果遇到超大的数据量,即使是O(N)的时间复杂度,蓄水池抽样程序完成抽样任务也将耗时很久。因此分布式的蓄水池抽样算法应运而生。运作原理如下:
- 假设有K台机器,将大数据集分成K个数据流,每台机器使用单机版蓄水池抽样处理一个数据流,抽样m个数据,并最后记录处理的数据量为N1, N2, …, Nk, …, NK(假设m
- 取[1, N]一个随机数d,若d
- 取[1, N]一个随机数d,若d
作者:邱simple
链接:https://www.jianshu.com/p/7a9ea6ece2af
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
埋个坑2:
- 分布式蓄水池抽样
基本的蓄水池抽样要求对数据流进行顺序读取。要进行容量为k的分布式蓄水池抽样(前面讨论的容量都为1),对于集合中的每一个元素,都产生一个0-1的随机数,之后选取随机值最大的前k个元素。这种方法在对大数据集进行分层抽样的时候非常管用。
- 加权分布式蓄水池抽样
集合中的数据是有权重的,算法希望数据被抽样选中的概率和该数据的权重成比例。对于每个数据计算一个0-1的值R,并求r的n次方根作为该数据的新的R值。这里的n就是该数据的权重。最终算法返回前k个R值最高的数据然后返回。根据计算规则,权重越大的数据计算所得的R值越接近1,所以越有可能被返回。

