线性的质数判断——欧拉筛法

质数本身这个概念很简单，要找因子只有1和它本身的数，最简单的求法就是1到根号n遍历判断因子，单次判断要根号n；

如果要遍历1到n的话，复杂度是O(n^3/2)，处理小规模的数据没问题，但是大规模就会比较慢。

当然如果只要判断一个数，那直接用这个就很快；

蒋委员长说过一句名言：以空间换时间，这个决策在历史上被人臭骂，但是在计算机领域确实是个很不错的思想，因为大部分情况时间复杂度比空间要宝贵的多。

那么这里就有一种以空间换时间的方法，叫筛法；

筛法的基础思想就是当我们遍历从2开始的数时，每遍历一个，把它的倍数全部标记了，后面就不用重复判断了，因为被标记就意味着是1和其本身以外的数的倍数，那就不符合质数的定义了。这个其实就是Eratosthenes筛法，最朴素的筛法，要介绍欧拉筛法，需要先理解这个朴素的筛法。

Eratosthenes筛法

筛法是Eratosthenes（下称埃氏），一个生活在公元前300年左右的希腊数学家发明的，时间复杂度为O(nloglogn)，但是需要先建立大数组去存下范围内所有的数，所以空间复杂度高于直接用根号法遍历。

具体做法是，假设范围是N，先建立一个数组，开到比N大一点，下标就表示2到N的每一个数，下标对应的值表示这个下标是否被标记，也就是它是否是合数，全部初始化为1。然后i从2开始遍历，标记i所有的倍数的值为0，比如2的倍数4，6，8……，3的倍数6，9……，被标记的数因为有了非1和本身的因子所以是合数。

当遍历到一个数没有被标记时，说明比它小的数中没有它的因数，那么它就是质数了（当然它的倍数还是要标记的），可以记入一个专门存放质数的数组里，这样就可以建立一个从1到N的质数查询表。

我在网上找到了一张非常直观的动图可以来展示这个过程

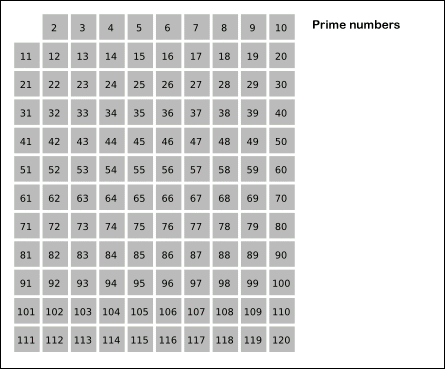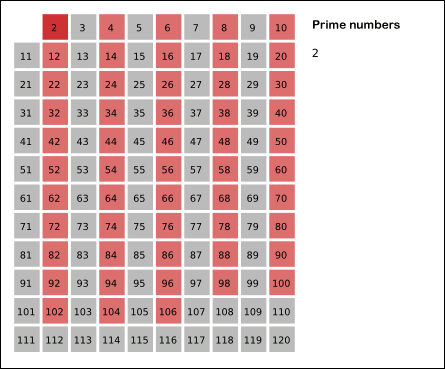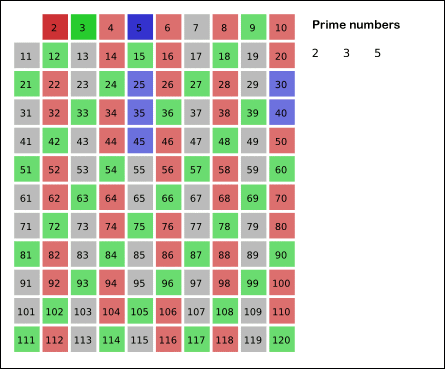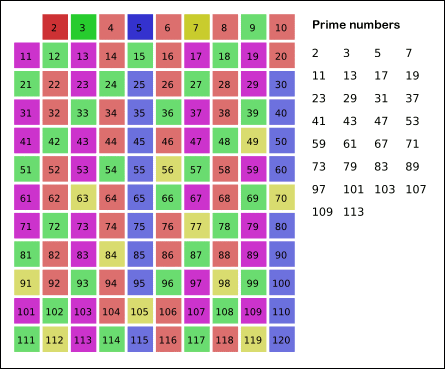
这个思路相对简单，在具体做法那一段已经基本上按照写代码的思路讲解了一遍了，那么现在就直接，上代码！

#include
#include
 
const int N = 100;//看题目范围改就行 
bool isPrime[N];//标记数组，类型是bool或者int都行，只存01值标记用 
int primes[N];//存质数的数组 
//当然，当数据太大导致普通数组存不下的时候，可以采用stl里的vector来存
int cnt;
 
void judgePri()
{
	memset(isPrime, 1, sizeof(isPrime));
	cnt = 0;
	isPrime[1] = 0;//把1排除掉，既不是质数也不是合数 
	for (int i = 2; i < N; i++) //从i到N遍历
	{
		if (isPrime[i] == 1)
		{
			primes[cnt++] = i;
			for (int j = i; j < N; j += i) //标记i在N范围内的所有倍数
			{
				isPrime[j] = 0;
			}
		}
	}
}
 
int main(void)
{
	judgePri();
	for (int i = 0; i < cnt; i++)
	{
		printf("%d ", primes[i]);
	}
	return 0;
}

但是很显然，这种算法虽然比根号法快，而且思路也比较简单，但是在遍历的时候依旧会有重复的情况，比如i=2，2的倍数中有6，6被标记了一次，3的倍数中有6，6又被标记了一次，那么这两次标记操作的重复就是一种浪费，所以如果有更高的速度追求，还得对这个朴素的埃氏筛法进行改进。

欧拉，对，就是那个在数学课里无处不在的天才高产数学家，他对筛法进行了改进，发明了一种可以实现O(n)时间复杂度线性解决质数筛选问题的方法，称为欧拉筛法，或者线性筛法。

欧拉筛法

欧拉筛法是在埃氏筛法的基础上，针对一个数的倍数可能被重复标记的问题进行了优化，思路大体如下：

与朴素的筛法相似，当i是质数的时候（也就是前面遍历过来没有被标记），依旧将其存入primes数组里面，随后，标记i的倍数是否是合数的方法要进行调整。

在埃氏筛法里，是将i的倍数全部标记，会导致的重复就是，一个合数可能有好几个因数，然后遍历到这个因数，就会被标记一次，例如12=2 * 6，12=3 * 4，那么遍历到2，3，4，6时12都会被标记一次。那么很自然的想法就是，我希望只用合数其中一个因数去筛掉这个合数。

在整数中，除了1，不是质数就是合数，而且任何合数都能表示成多个质数的积，这句话是构建合数的基础，是一个基本定理。

依托这个定理转换一下思路，因为我们会把到 i 之前的质数存下来，我们完全可以利用已知的质数，去找这些质数的倍数来标记出合数，而不是无脑的碰到一个数就标记其倍数，这个时候，i 不知道是质数还是合数，但是 i * primes一定是个合数，也就是，思路转变成了，把已经找到的质数的倍数，全部标记成合数。

因为质数是被存下来的，我们从已知的质数表从头开始（也就是设j从0开始一直到当前的cnt为止），这个时候prime[j]是从小到大找质数的，可以用i%prime[j]==0来表示此时的质数是否是i的因子，一旦找到了，那便是最小的质数因子（因为从小到大遍历质数表），假设遍历到了prime[j]，那么 i 这个合数就被其中一个因子prime[j]标记了，直接跳出循环，这样就能保证每个合数只被其最小的质数因子标记。

这个时候虽然 i 乘以prime[j]之后的质数还没有被标记成合数，比方说 i *prime[k]（k>j）也是合数，但是随着 i 的推进，此前的 i *prime[k] 这个值会被 不断变大的 i 遍历的过程中被更大的质数因子筛去，这里观察一下打表的情况就能理解了。

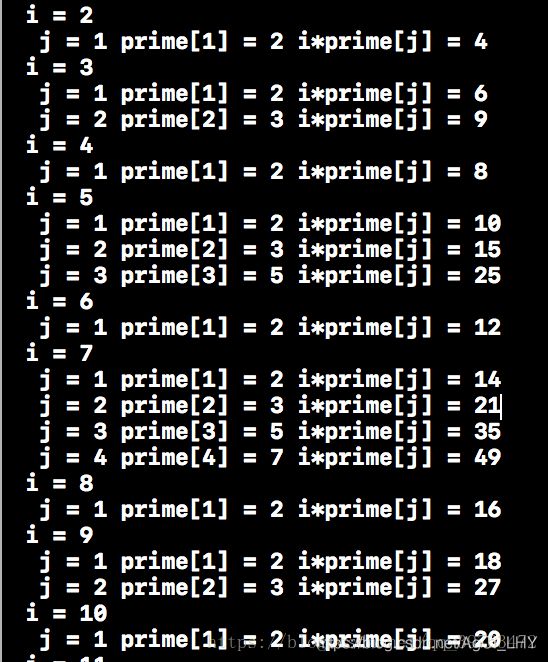
图片来自https://blog.csdn.net/qq_39763472/article/details/82428602

i=2时，尽管只到2乘2（prime[1]）就跳出循环了，而2乘3(prime[2])能排掉6，但是随着i变大，当i变成了那个prime[2]的时候，6依旧会被排掉。

下面是代码，建议和上文的介绍对照着看

#include
#include
 
const int N = 100;
bool isPrime[N];
int primes[N];
 
int cnt;
 
void judgePri() 
{
	int temp;
	memset(isPrime, 1, sizeof(isPrime));
	cnt = 0;
	isPrime[1] = 0;
	for (int i = 2; i < N; i++)
	{
		if (isPrime[i] == 1)
		primes[cnt++] = i;
		//精髓 
		for (int j = 0; j < cnt && (temp = i * primes[j]) < N; j++) //找i之前的所有质数 
		{
			isPrime[temp] = 0;//i * primes[j]肯定是合数，先标记掉 
			if (i % primes[j] == 0)//关键，每次整除一个最小的质数将会跳出循环，所以每个数字，只会被最小的质数筛一次 
			{
				break;
			}
		}
		//精髓  
	}
}
 
int main(void)
{
	judgePri();
	for (int i = 0; i < cnt; i++)
	{
		printf("%d ", primes[i]);
	}
	return 0;
}