【AcWing】AcWing 5183. 好三元组（秋季每日一题2023）（枚举 + 组合数学 + 圆上前缀和）

题目

https://www.acwing.com/problem/content/5186/

题目大意：给定一个圆上若干个点（可能有重复）。从中任取3个点，要求组成的三角形包含圆心。

思路

问题转化

如果直接求圆心在三角形内部的方案数，其实不太好求。所以尝试反过来求，求不在三角形内部的方案数，然后用总方案数减去即可得到答案（这也是排列组合里一个常用的思想）。总方案数其实很容易，就是$C_n^3$，$n$表示所有点的数量。对于不在三角形内部的方案数分析如下。

仔细思考一下，其实很难直接通过一个公式去计算出来。那这个时候我们可以先固定1个点，看一下另外2个点的怎么去选（这里就是一个枚举的思想，先枚举其中1个点，之后就可以聚焦到对于这个点来说，如何去求另外2个点，使得圆心不在三角形内部）。

枚举求圆心不在三角形内部的方案

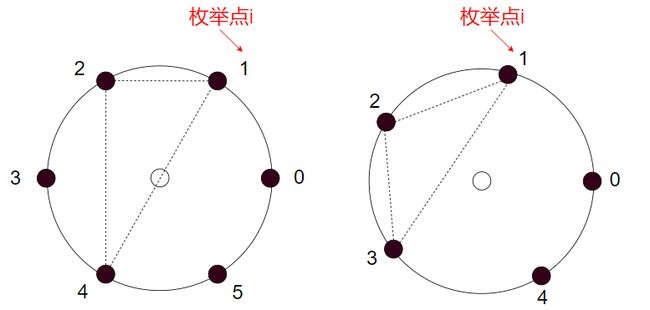
当固定1个点（枚举点）时，3个点的选法分三种情况：3个点都选在了枚举点的位置、只有2个点选在了枚举点的位置、只有1个点选在了枚举点的位置。如下图：

为避免方案重复，我们可以人为规定，选取的另外两个点的下标在枚举点的下标右侧（或者和枚举点重合），则选取的三个点要么在下标为$i$的位置取，要么在区间$(i,i+c/2]$中取，且下标为i的位置至少取1个。现在就可以用组合数来表示方案数了：

• 在$i$位置取1个点，在$(i,i+(c-1)/2]$中取2个点，方案数为$C(cnt[i],1)\ast C(s[i,i+(c-1)/2],2)$
• 在$i$位置取2个点，在$(i,i+(c-1)/2]$中取1个点，方案数为$C(cnt[i],2)\ast C(s[i,i+(c-1)/2],1)$
• 在$i$位置取3个点，在$(i,i+(c-1)/2]$中取0个点，方案数为$C(cnt[i],3)\ast C(s[i,i+(c-1)/2],0)$

其中$cnt[i]$表示位置$i$有多少个点，s[i, j]$表示下标从$i$到$j$中一共有多少个数。求一个区间中有多少个数，那这里很容易联想到前缀和。由于这是在一个圆上，所以需要用到破环成链的思想来维护前缀和。至此，我们的方案数为

$$C_n^3-C(cnt[i],1)\ast C(s[i,i+(c-1)/2],2)-C(cnt[i],2)\ast C(s[i,i+(c-1)/2],1)-C(cnt[i],3)\ast C(s[i,i+(c-1)/2],0)$$

去掉特殊情况

另外，当$c$为偶数的时候，有两种情况被重复算了两次：

如上图，当3个点都在直径上的时候，我们会先枚举位置1，再枚举位置4。比如先枚举位置1，那么有两种情况：

• 位置1取1个点，位置4取2个点
• 位置1取2个点，位置4取1个点

再枚举4，也有两种情况：

• 位置4取1个点，位置1取2个点
• 位置4取2个点，位置1取1个点

这实际上重复计算了，被减了两次。所以最后我们还需要加上一次。实现上，当$c$取偶数的时候，我们再次遍历一个半圆，把方案数加上即可，方案为$C(cnt[i],2)\ast C(cnt[i+m/2],1)$和$C(cnt[i],1)\ast C(cnt[i+m/2],2)$。

最终算法

所以最终算法如下：

1. 求$C_n^3$
2. 遍历圆上的所有点，每次从$C_n^3$中减去$C(cnt[i],1)\ast C(s[i,i+(c-1)/2],2)$、$C(cnt[i],2)\ast C(s[i,i+(c-1)/2],1)$、$C(cnt[i],3)\ast C(s[i,i+(c-1)/2],0)$
3. 如果$c$为偶数，遍历半个圆，每次再从答案中加上$C(cnt[i],2)\ast C(cnt[i+m/2],1)$和$C(cnt[i],1)\ast C(cnt[i+m/2],2)$

圆心在三角形边上

#include 

using namespace std; 

typedef long long LL;

const int N = 2000010; // 圆形前缀和注意范围要 * 2

int n, m;
int cnt[N], s[N];

LL C(int a, int b) { // 求组合数
    LL res = 1;
    for(int i = a, j = 1; j <= b; i --, j ++ ) {
        res = res * i / j;
    }
    return res;
}

int main() {
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i ++ ) {
        int p;
        scanf("%d", &p);
        cnt[p] ++, cnt[p + m] ++ ; // 统计每个点的数量
    }
    
    for(int i = 1; i < 2 * m; i ++ ) s[i] = s[i - 1] + cnt[i];  // 前缀和
    
    // 总的方案数
    LL res = C(n, 3); 
    
    // 枚举求圆心不在三角形内部的方案
    for(int i = 0; i < m; i ++ ) {
        int x = s[i + m / 2] - s[i]; // (i, i + m /2]的点的数量
        int y = cnt[i]; // i位置点的数量(每个位置可能有多个点)
        res = res - (C(y, 3) * C(x, 0) + C(y, 2) * C(x, 1) + C(y, 1) * C(x, 2));
    }
    
    // 特殊情况
    if (m % 2 == 0) {
        for(int i = 0; i < m /2; i ++ ) {
            res = res + (LL)C(cnt[i], 2) * C(cnt[i + m / 2], 1); 
            res = res + (LL)C(cnt[i], 1) * C(cnt[i + m / 2], 2); 
        }
    }
    
    printf("%lld\n", res);
    
    return 0;
}

总结

• 在组合数学的题目里，正着不好求可以反过来求
• 求解涉及到多个元素组合出一种方案的问题，如果觉得不太好求，可以尝试先固定其中一个元素（固定其实就是枚举），然后着重思考另外几个元素
• 对于圆形上的前缀和问题，要用破环成链的思想