算法训练Day39 | LeetCode62. 不同路径;LeetCode63.不同路径II
目录
LeetCode62. 不同路径
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
LeetCode63.不同路径II
1. 思路
2. 代码实现
3. 复杂度分析
4. 思考与收获
LeetCode62. 不同路径
链接: 62. 不同路径 - 力扣(LeetCode)
1. 思路
机器人从(0 , 0) 位置出发,到(m - 1, n - 1)终点。
按照动规五部曲来分析:
1.1 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径;
1.2 确定递推公式
想要求dp[i][j],只能有两个方向来推导出来,即dp[i - 1][j] 和 dp[i][j - 1];
此时在回顾一下 dp[i - 1][j] 表示啥,是从(0, 0)的位置到(i - 1, j)有几条路径,dp[i][j - 1]同理;
那么很自然,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来;
1.3 dp数组的初始化
如何初始化呢,首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理;
所以初始化代码为:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
1.4 确定遍历顺序
这里要看一下递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1],dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了;
这样就可以保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值的;
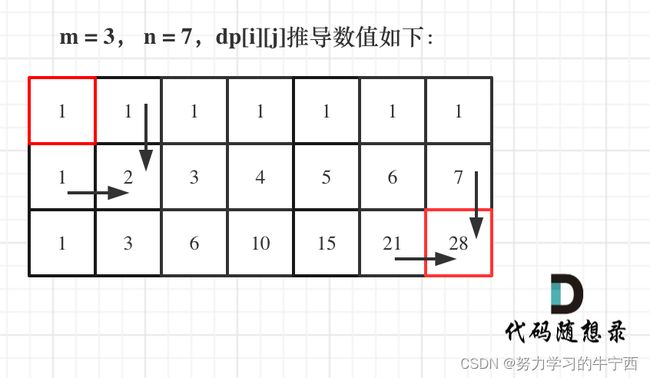
1.5 举例推导dp数组
2. 代码实现
# 经典动态规划
# time:O(m*n);space:O(m*n)
class Solution(object):
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
# dp[i][j]表示到(i,j)位置的路径方法为dp[i][j]种
dp = [[0 for i in range(n)] for j in range(m)]
# 初始化,dp的第0行和第0列的数值全部为1,只有一种路径
for x in range(m): dp[x][0] = 1
for y in range(n): dp[0][y] = 1
# 从上到下,从左到右遍历
for x in range(1,m):
for y in range(1,n):
dp[x][y] = dp[x-1][y]+dp[x][y-1]
# 最右下角的值即为答案
return dp[m-1][n-1]
3. 复杂度分析
-
时间复杂度:O(m*n)
网格的大小为m x n ;for loop需要从左到右,从上到下,把所有格子都遍历一次,每次操作一个加法运算;
-
空间复杂度:O(m*n)
dp数组是一个二维数组,大小和网格一样也为m x n;
4. 思考与收获
-
(二刷再看)深度搜索做法
这道题目,刚一看最直观的想法就是用图论里的深搜,来枚举出来有多少种路径。
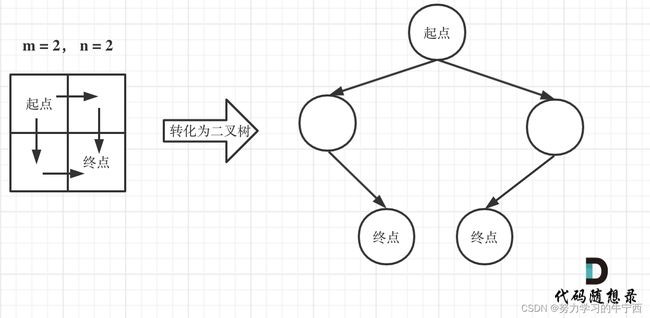
注意题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
class Solution { private: int dfs(int i, int j, int m, int n) { if (i > m || j > n) return 0; // 越界了 if (i == m && j == n) return 1; // 找到一种方法,相当于找到了叶子节点 return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n); } public: int uniquePaths(int m, int n) { return dfs(1, 1, m, n); } };大家如果提交了代码就会发现超时了!
来分析一下时间复杂度,这个深搜的算法,其实就是要遍历整个二叉树。
这棵树的深度其实就是m+n-1(深度按从1开始计算)。
那二叉树的节点个数就是 2^(m + n - 1) - 1。可以理解深搜的算法就是遍历了整个满二叉树(其实没有遍历整个满二叉树,只是近似而已)
所以上面深搜代码的时间复杂度为O(2^(m + n - 1) - 1),可以看出,这是指数级别的时间复杂度,是非常大的。
-
(二刷再看) 数论的做法
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步;
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么有几种走法呢? 可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
那么这就是一个组合问题了。
求组合的时候,要防止两个int相乘溢出! 所以不能把算式的分子都算出来,分母都算出来再做除法。
例如如下代码是不行的。
class Solution {
public:
int uniquePaths(int m, int n) {
int numerator = 1, denominator = 1;
int count = m - 1;
int t = m + n - 2;
while (count--) numerator *= (t--); // 计算分子,此时分子就会溢出
for (int i = 1; i <= m - 1; i++) denominator *= i; // 计算分母
return numerator / denominator;
}
};
需要在计算分子的时候,不断除以分母,代码如下:
class Solution {
public:
int uniquePaths(int m, int n) {
long long numerator = 1; // 分子
int denominator = m - 1; // 分母
int count = m - 1;
int t = m + n - 2;
while (count--) {
numerator *= (t--);
while (denominator != 0 && numerator % denominator == 0) {
numerator /= denominator;
denominator--;
}
}
return numerator;
}
};
- 时间复杂度:O(m)
- 空间复杂度:O(1)
计算组合问题的代码还是有难度的,特别是处理溢出的情况
Reference: 代码随想录 (programmercarl.com)
本题学习时间:60分钟。
LeetCode63.不同路径II
链接:63. 不同路径 II - 力扣(LeetCode)
1. 思路
本题相对于9.4 不同路径 就是多了障碍物,第一次接触这种题目的同学可能会有点懵,这有障碍了,应该怎么算呢?
我们已经详细分析了没有障碍的情况,有障碍的话,其实就是标记对应的dp table(dp数组)保持初始值(0)就可以了;
动态规划五部曲
1.1 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径;
1.2 确定递推公式
递推公式和 9.4 不同路径 一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1],
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0);
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
1.3 dp数组如何初始化
在 9.4 不同路径 我们把第0行和第0列全部初始化为1;因为从(0, 0)的位置到(i, 0)的路径只有一条,所以dp[i][0]一定为1,dp[0][j]也同理。
但在本题中,如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0;下标(0, j)的初始化情况同理;
注意代码里for循环的终止条件,一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作,dp[0][j]同理;
1.4 确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值;
1.5 举例推导dp数组
拿示例1来举例如题:
对应的dp table 如图:
2. 代码实现
实现方法1:二维数组
# 动态规划
# time:O(m*n);space:O(m*n)
class Solution(object):
def uniquePathsWithObstacles(self, obstacleGrid):
"""
:type obstacleGrid: List[List[int]]
:rtype: int
"""
# 如果最左上角就是一个障碍物的话,直接到不了右下角了
if obstacleGrid[0][0] == 1: return 0
# 创建一个dp数组
row = len(obstacleGrid)
col = len(obstacleGrid[0])
dp = [[0 for i in range(col)] for j in range(row)]
# 初始化第0列
for x in range (row):
if obstacleGrid[x][0] != 1:
dp[x][0] = 1
else:
break
# 初始化第0行
for y in range(col):
if obstacleGrid[0][y] != 1:
dp[0][y] = 1
else:
break
# 开始遍历,从左至右,从上至下,记得检查是否为障碍
for x in range(1,row):
for y in range(1,col):
if obstacleGrid[x][y] != 1:
dp[x][y] = dp[x][y-1] + dp[x-1][y]
return dp[row-1][col-1]
实现方法2:一维数组
# 动态规划 空间优化版本
# time:O(m*n);space:O(n)
class Solution(object):
def uniquePathsWithObstacles(self, obstacleGrid):
"""
:type obstacleGrid: List[List[int]]
:rtype: int
"""
# 网格的大小为m行n列
m = len(obstacleGrid)
n = len(obstacleGrid[0])
# 初始化dp数组,只保存当前行
cur = [0]*n
# 先初始化为第一行
for j in range(n):
if obstacleGrid[0][j] != 1:
cur[j] = 1
else: break
# 开始遍历,从第二行开始
for i in range(1,m):
# 从第一列开始,因为第一列可能有障碍物
for j in range(n):
if obstacleGrid[i][j] == 1:
cur[j] = 0
# 当j=0,obstacleGrid[i][j]!=1的时候
# 不需要处理,只用维持和之前一样就行
# 前面是0就是0,前面是1就是1
# 隐含的状态更新
# dp[i][0] = dp[i - 1][0]
elif j>0:
# 等价于dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
cur[j] = cur[j]+cur[j-1]
return cur[-1]
3. 复杂度分析
实现方法1:二维数组
-
时间复杂度:O(m*n)
网格的大小为m x n ;for loop需要从左到右,从上到下,把所有格子都遍历一次,每次操作一个加法运算;
-
空间复杂度:O(m*n)
dp数组是一个二维数组,大小和网格一样也为m x n;
实现方法2:一维数组
-
时间复杂度:O(m*n)
n、m 分别为obstacleGrid 长度和宽度 ;for loop需要从左到右,从上到下,把所有格子都遍历一次,每次操作一个加法运算;
-
空间复杂度:O(n)
n、m 分别为obstacleGrid 长度和宽度,优化空间,不需要记录mxn 的二维数组,dp数组是一个一维数组,大小为n;
4. 思考与收获
- 本题是9.4 不同路径的有障碍版,整体思路大体一致。但就算是做过9.4.不同路径,在做本题也会有感觉遇到障碍无从下手;其实只要考虑到,遇到障碍dp[i][j]保持0就可以了;
- 也有一些小细节,例如:初始化的部分,很容易忽略了障碍之后应该都是0的情况;
- Python中for循环(continue,break,pass)
-
continue 跳过当前继续执行下一个循环;
l = ['a','b','c','d','e'] for i in l: #i遍历l列表中的每一个元素 if i == 'c': # continue以下的代码不执行直接进入下一个循环 continue print(i)output :
a b d e -
break 直接中断循环,不再执行;
l = ['a','b','c','d','e'] for i in l: if i == 'c': # break直接跳出循环,break以下代码全部不执行 break print(i)output:
a b -
pass 什么都不操作,接着循环;
l = ['a','b','c','d','e'] for i in l: #i遍历l列表中的每一个元素 if i == 'c': pass print(i)output:
a b c d e
-
Reference: 代码随想录 (programmercarl.com)
本题学习时间:90分钟。
本题学习时间近3小时,总结字数5000+;做动态规划的第二天,接触到了二维的dp,对动态规划有了更深刻的理解,两道题做法类似,只是加不加障碍物的区别。(求推荐!)