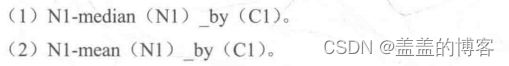工业蒸汽量预测（速通三）

特征优化

1特征优化的方法

可以通过合成特征、对特征做简单变换、用决策树创造新特征、特征组合等方法对特征进行优化。

1.1合成特征

合成特征是指不在输入特征之列，而是丛一个或多个输入特征衍生而来的特征。通过标准化或缩放单独创建的特征不属于合成特征。

合成特征包括以下类型:

(1)将一个特征与其本身或其他特征相乘(称为特征组合)。

(2)两个特征相除。

(3)对连续特征进行分桶(分箱)，以分为多个区间分箱。

1.2特征的简单变换

数值特征的变换和组合：

任何针对单独特征列的单调变换(如对数),都不适用于决策树类算法。

特征的线性组合(linear combination)仅适用于决策树以及基于决策树的集成学习算法(如Gradient Boosting,随机森林)，因为树模型不擅长捕获不同特征之间的相关性。而SVM、线性回归、神经网络等模型自身可以线性组合。

常用的数值特征的变换和组合如下:

类别特征与数值特征的组合：

仅仅将已有的类别特征和数值特征进行以上的有效组合，就能增加大量优秀的可用特征。如果将这种方法和线性组合等基础特征工程方法结合(仅用于决策树)，则可以得到更多有意义的特征，如下:

//特征构造
epsilon = 1e-5
func_dict = {
    'add':lambda x,y:x + y,
    'mins':lambda x,y:x - y,
    'div':lambda x,y:x/(y+epsilon),
    'multi':lambda x,y:x * y,
}

def auto_features_make(train_data, test_data,func_dict, col_list):
    train_data, test_data = train_data.copy(),test_data.copy()
    for col_i in col_list:
        for col_j in col_list:
            for func_name,func in func_dict.items():
                for data in [train_data,test_data]:
                    func_features = func(data[col_i], data[col_j])
                    col_func_features = '-'.join([col_i, func_name, col_j])
                    data[col_func_features] = func_features
    return train_data, test_data

1.3用决策树创造新特征

1.4特征组合

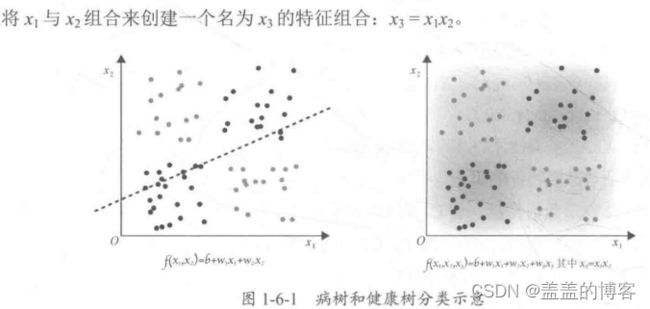
特征组合是指通过将单独的特征进行组合(相乘或求笛卡儿积)而形成的合成特征，其有助于表示非线性关系。

对非线性规律进行编码：

组合独热矢量：

使用分桶特征列训练模型：

分桶特征:是以一定方式将连续型数值特征划分到不同的桶(箱)中，可以理解为是对连续型特征的一种离散化处理方式。

举例说明，我们可以将某地的人口(population) 特征分为以下3个分桶:

bucket_ 0 (< 5000):对应人口分布较少的街区。
bucket_ 1 (5000~ 25000):对应人口分布适中的街区。
bucket 2 (> 25000):对应人口分布较多的街区。

模型融合

1模型优化

在选择一个模型进行训练后，如何判断模型的优劣及优化模型的性能呢?

一般可以从以下几方面进行优化:研究模型学习曲线，判断模型是否过拟合或者欠拟合并做出相应的调整;对模型权重参数进行分析，对于权重绝对值高或低的特征，可以进行更细化的工作，也可以进行特征组合:进行Bad-Case分析，针对错误的例子确定是否还有地方可以修改挖掘:进行模型融合。

1.1模型学习曲线

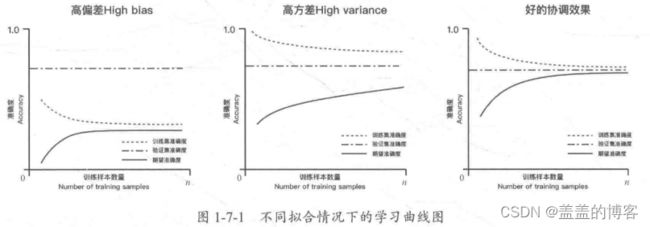
出现高偏差，表明模型太过简单，没有能力学习到样本的底层规律，此时训练集和验证集的准确率都会很低。

出现高方差，表明模型太过复杂，学习太过，在训练集上的准确率较好，但是在验证集上的泛化能力较差，验证集的准确率较低，两个准确率相差较大。

1.2模型融合提升技术

模型融合，即先产生一组个体学习器，再用某种策略将它们结合起来，以加强模型效果。

按照个体学习器的关系，模型融合提升技术可以分为两类:

(1)个体学习器间不存在强依赖关系可同时生成的并行化方法，代表是Bagging 方法和随机森林。

(2)个体学习器间存在强依赖关系必须串行生成的序列化方法，代表是Boosting方法。

Bagging 方法和随机森林：

Bagging方法是从训练集中抽样得到每个基模型所需要的子训练集,然后对所有基模型预测的结果进行综合，产生最终的预测结果，如图1-7-3所示。

Bagging方法采用的是自助采样法( Bootstrap sampling),即对于m个样本的原始训练集，每次先随机采集一 个样本放入采样集，接着把该样本放回，也就是说下次采样时该样本仍有可能被采集到，这样采集m次，最终可以得到m个样本的采样集。由于是随机采样，因此每次的采样集和原始的训练集不同，和其他采样集也不同，这样就可以得到多个不同的弱学习器。

随机森林是对Bagging方法的改进，其改进之处有两点:基本学习器限定为决策树;除了在Bagging的样本上加上扰动，在属性上也加上扰动，相当于在决策树学习的过程中引入了随机属性选择。对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含 k个属性的子集，然后从这个子集中选择一个最优属性用于划分。

#将LinearRegression，LGB，RandomForestRegressor三个模型融合
# 3个模型融合
def model_mix(pred_1, pred_2, pred_3):
    result = pd.DataFrame(columns=['LinearRegression', 'LGB', 'RandomForestRegressor', 'Combine'])

    for a in range(10):
        for b in range(10):
            for c in range(1,10):
                test_pred = (a * pred_1 + b * pred_2 + c * pred_3) / (a + b + c)

                mse = mean_squared_error(test_target, test_pred)

                result = result.append([{'LinearRegression': a,
                                         'LGB': b,
                                         'RandomForestRegressor': c,
                                         'Combine': mse}],
                                       ignore_index=True)
    return result


model_combine = model_mix(linear_predict, LGB_predict, RandomForest_predict)

model_combine.sort_values(by='Combine', inplace=True)
print(model_combine.head())

Boosting方法：

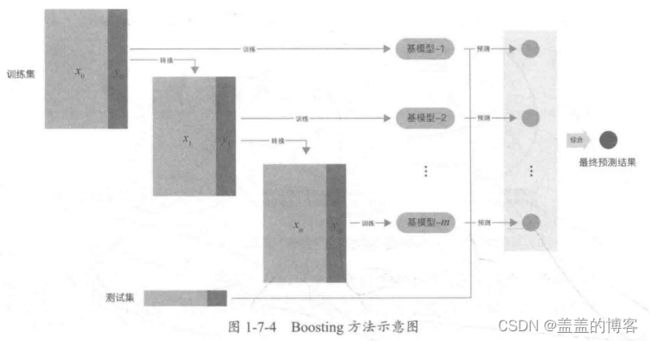
Boosting方法的训练过程为阶梯状，即基模型按次序一一进行训练(实现上可以做到并行)，基模型的训练集按照某种策略每次进行一定的转换，然后对所有基模型预测的结果进行线性综合，产生最终的预测结果，如图1-7-4所示。

Boosting方法中著名的算法有AdaBoost算法和提升树(Boosting Tree)系列算法。在提升树系列算法中，应用最广泛的是梯度提升树(Gradient Boosting Tree)，下 面逐一简要介绍。

(1) AdaBoost算法:是加法模型、损失函数为指数函数、学习算法为前向分布算法时的
二分类算法。

(2)提升树:是加法模型、学习算法为前向分布算法时的算法，基本学习器限定为决策树。对于二分类问题，损失函数为指数函数，就是把AdaBoost算法中的基本学习器限定为二叉决策树:对于回归问题，损失函数为平方误差，此时拟合的是当前模型的残差。

(3)梯度提升树:是对提升树算法的改进。提升树算法只适合于误差函数为指数函数和平方误差，而对于一般的损失函数，梯度提升树算法可以将损失函数的负梯度在当前模型的值作为残差的近似值。

model = 'GradientBoosting'
metal_models[model] = GradientBoostingRegressor()

param_grid = {'n_estimators':[150,250,350],
              'max_depth':[1,2,3],
              'min_samples_split':[5,6,7]}

metal_models[model], cv_score, grid_results = train_model(metal_models[model], param_grid=param_grid, X=metal_x_train,y=metal_y_train,
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

model = 'XGB'
metal_models[model] = XGBRegressor()

param_grid = {'n_estimators':[100,200,300,400,500],
              'max_depth':[1,2,3],
             }

metal_models[model], cv_score,grid_results = train_model(metal_models[model], param_grid=param_grid, X=metal_x_train,y=metal_y_train,
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

1.3预测结果融合策略

Voting：

Voting (投票机制)分为软投票和硬投票两种，其原理采用少数服从多数的思想，此方法可用于解决分类问题。

(1)硬投票:对多个模型直接进行投票，最终投票数最多的类为最终被预测的类。

(2)软投票:和硬投票原理相同，其增加了设置权重的功能，可以为不同模型设置不同
权重，进而区别模型不同的重要度。

Averaging和Ranking：

Averaging的原理是将模型结果的平均值作为最终的预测值，也可以使用加权平均的方法。但其也存在问题:如果不同回归方法预测结果的波动幅度相差比较大，那么波动小的回归结果在融合时起的作用就比较小。

Ranking的思想和Averaging的一致。 因为上述平均法存在一定的问题， 所以这里采用了把排名平均的方法。如果有权重，则求出n个模型权重比排名之和，即为最后的结果。

Blending：

Blending是把原始的训练集先分成两部分，如70%的数据作为新的训练集，剩下30%的数据作为测试集。

在第一层中，我们用70%的数据训练多个模型，然后去预测剩余30%数据的label。在第二层中，直接用30%的数据在第一层预测的结果作为新特征继续训练即可。

Blending的优点: Blending比Stacking简单(不用进行k次交叉验证来获得stacker feature),避开了一些信息泄露问题，因为generlizers和stacker使用了不一样的数据集。

Blending的缺点:
(1)使用了很少的数据(第二阶段的blender只使用了训练集10%的数据量)。
(2) blender 可能会过拟合。

说明:对于实践中的结果而言，Stacking 和Blending的效果差不多。

Stacking：

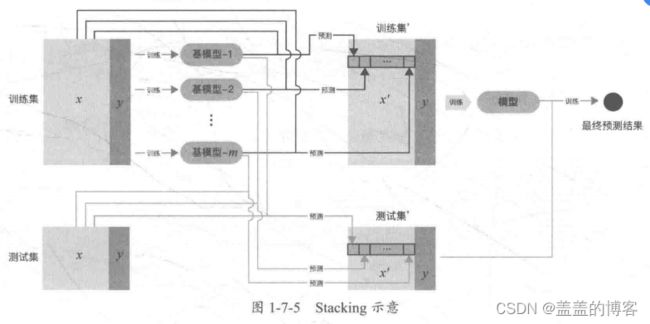
Stacking的基本原理是用训练好的所有基模型对训练集进行预测，将第j个基模型对第i个训练样本的预测值作为新的训练集中第i个样本的第j个特征值，最后基于新的训练集进行训练。同理，预测的过程也要先经过所有基模型的预测形成新的测试集，最后对测试集进行预测，如图1-7-5所示。

Stacking是一种分层模型集成框架。以两层为例:第一层由多个基学习器组成，其输入为原始训练集;第二层的模型则是以第一层基学习器的输出作为训练集进行训练，从而得到完整的Stacking模型。

Stacking 两层模型都使用了全部的训练集数据。

说明:在做Stacking 的过程中，如果将第一层模型的预测值和原始特征合并加入第二层模型的训练中，则可以使模型的效果更好，还可以防止模型的过拟合。

1.4其他提升方法

通过对权重或者特征重要性的分析，可以准确找到重要的数据和字段及相关的特征方向，并可以朝着此方向继续细化，同时寻找这个方向更多的数据，还可以做相关的特征组合，这些都可以提高模型的性能。

通过Bad-Case分析，可以有效找到预测不准确的样本点，进而回溯分析数据，寻找相关的原因，从而找到提高模型精度的方法。