LeetCode 热题 HOT 100 第四十一天 114. 二叉树展开为链表 中等题 用python3求解

题目地址

给你二叉树的根结点 root ，请你将它展开为一个单链表：
展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

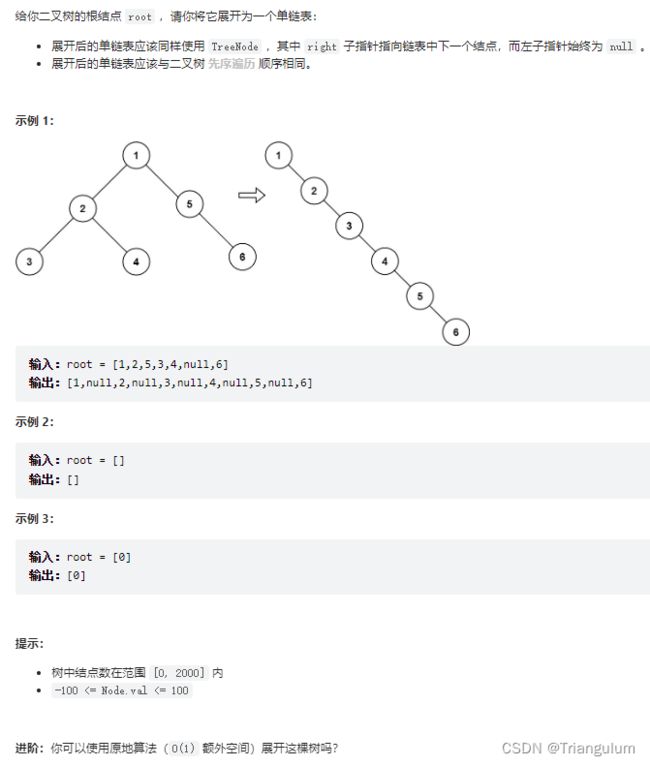
示例 1：
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：
输入：root = []
输出：[]

示例 3：
输入：root = [0]
输出：[0]

提示：
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？=

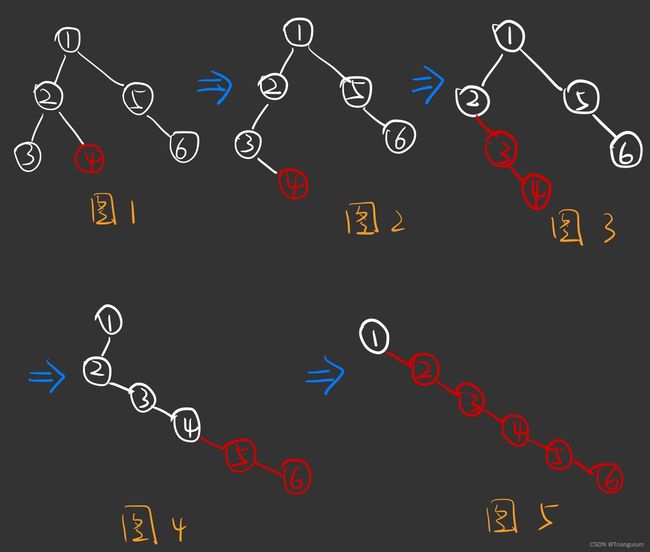
解法一: 后序遍历、递归

我们采用后序遍历的方式，也就是 左节点-右节点-打印根节点 这个顺序遍历二叉树。
当遍历到根节点后，我们对根节点的左右子树做一些调整。

    1
   / \
  2   3

将右节点挂到左节点的最右边

   1
  /
 2
  \
   3 

再将整个左子树挂到根节点的右边，这样就可以将整棵树变成链表结构了。

1
 \
  2
   \
    3

时间复杂度:O(N)
空间复杂度:O(h),h是树高度

以示例1为例，图解：

代码实现：

class Solution(object):
	def flatten(self, root):
		def dfs(root):
			if not root:
				return
			dfs(root.left)
			dfs(root.right)
			
			if root.left:
				pre = root.left
				while pre.right:
					pre = pre.right
				pre.right = root.right # 将右子树挂到 左子树的最右边 （对应图2、图4）
				root.right = root.left # 再将整个左子树挂到根节点的右边 （对应图3、图5）
				root.left = None
		dfs(root)

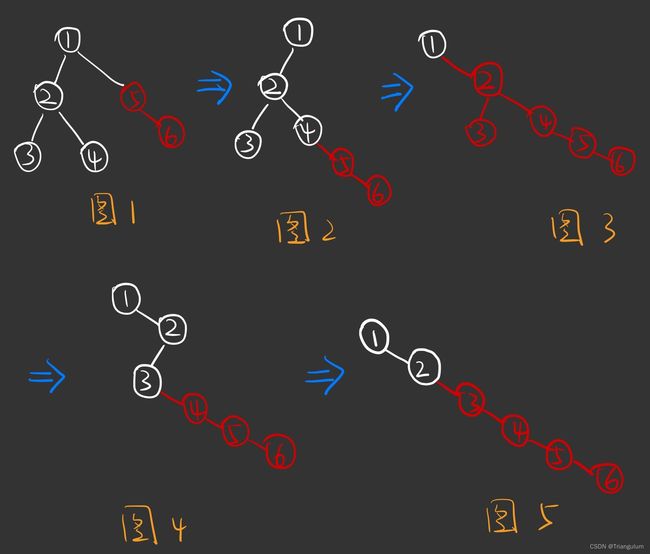
解法二: 非递归，不使用辅助空间及全局变量

前面的递归解法实际上也使用了额外的空间，因为递归需要占用额外空间。下面的解法无需申请栈，也不用全局变量，是真正的 In-Place 解法。

虽然代码看起来跟解法一差不多，但画一下图就知道这过程是不一样的。

以示例1为例，图解：

代码实现：

class Solution:
    def flatten(self, root):
        while root:
            if root.left:   #左子树存在的话才进行操作
                pre = root.left
                while pre.right:   #左子树的右子树找到最深
                    pre = pre.right
                pre.right = root.right #将root的右子树挂到左子树的右子树的最深（对应图2、图4）
                root.right = root.left      #将root的左子树挂到右子树（对应图3、图5）
                root.left = None            #将root左子树清空
            root = root.right               #继续下一个节点的操作