力扣--动态规划专题 I
题目列表
-
- 1.300-最长递增子序列
- 2. 剑指offer42.连续子数组的最大和
- 3.70--爬楼梯
- 4.413--等差数列划分
- 5.64--最小路径和
- 6. 542--01矩阵
- 7.221-最大正方形
- 8.1277-统计全为1的正方形子矩阵
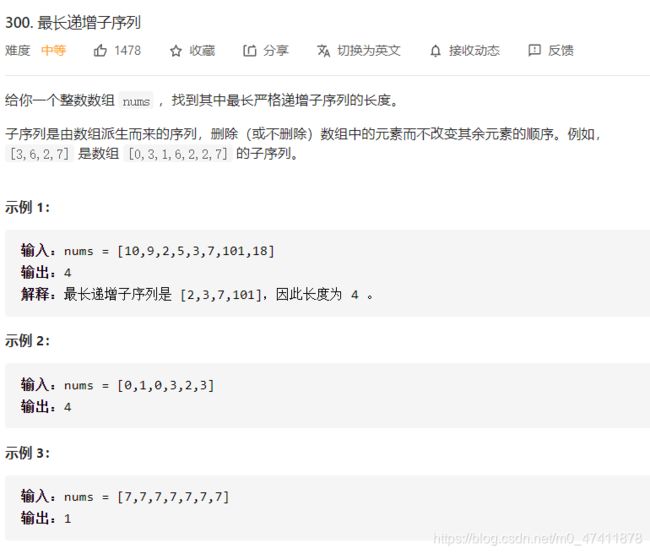
1.300-最长递增子序列
动态规划
构建一个与nums数组长度相等的dp数组,dp[i]为以第i个元素结尾的最长子序列的长度,并设置初值均为1。
遍历数组nums,当遍历到元素nums[i]时,dp[0…i-1]都被算出,所以dp[i]的状态转移方程为 dp[i] = max(dp[i], dp[j]+1), 0<=j
解释状态方程:遍历到nums[i]时,重新遍历nums[0…i-1]找到比nums[i]小的元素,因为只有比它小,才有可能增加子序列的长度。比nums[i]小的元素可能有很多,分别计算dp[j]+1,找到最大的dp[j]+1即[0…i-1]中比nums[i]小的元素的最长子序列长度。
得到完整的dp数组之后,找到其中的最大值,就是最长子序列长度
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n, 1);
for(int i = 1; i < n; i++){
for(int j = 0; j < i; j++){
if(nums[i]>nums[j]){
dp[i] = max(dp[i], dp[j]+1);
}
}
}
int m = dp[0];
for(int i = 1; i < n; i++){
if(m < dp[i]){
m = dp[i];
}
}
return m;
}
};
贪心+二分搜索
上一个算法的时间复杂度是O(n2),复杂度较高。
换一种思考方式,要让子序列尽可能地长,就要让子序列增加的尽可能地慢,也就是说让子序列的元素增加的尽可能地小,这是“贪心”思想。
构造数组d[i],代表长度为i的最长子序列末尾元素的最小值,d[1]=nums[0]。
d[i]数组是当单调递增的,证明:若d[3] = 5, d[5] = 3,长度为5的最长子序列的末尾元素是3,而长度为3的最长子序列长度为5,这肯定是不对的,因为能在长度为5的最长子序列中找到长度为3的最长子序列的末尾元素,并且该元素要小于3,所以d[i]数组是单调递增的。
算法步骤:
a.设len表示最长子序列长度,len初值为1,遍历整个数组nums[i]
b. 若nums[i]>d[len],则len长度加1,将nums[i]加入到d数组中.
c. 否则,找到d[i-1] < nums[j] < d[i],更新d[i] = nums[j],由于d数组是单调递增的,可以用二分查找搜索。
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size(), len = 1;
vector<int>d(n+1, 0);
d[len] = nums[0];
for(int i = 1; i < n; i++){
if(nums[i] > d[len]){
len++;
d[len] = nums[i];
}
else{
int low = 1, high = len, pos = 0;
while(low <= high){
int mid = (high+low) >> 1;
if(nums[i] > d[mid]){
pos = mid;
low = mid + 1;
}
else{
high = mid - 1;
}
}
d[pos+1] = nums[i];
}
}
return len;
}
};
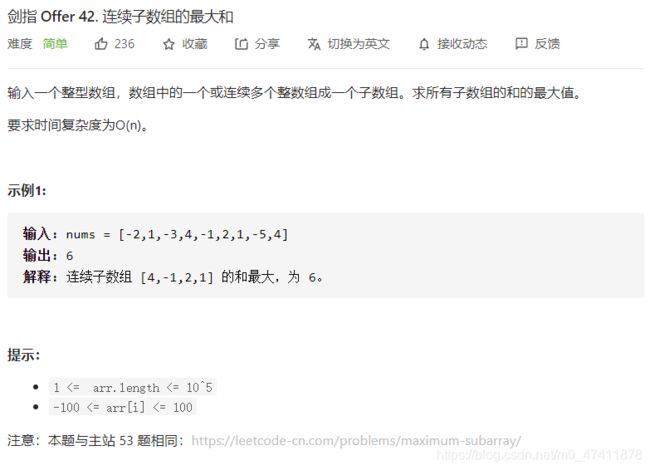
2. 剑指offer42.连续子数组的最大和
(2)题解:
动态规划
构建一个数组dp[i],代表以第i个元素结尾的连续子数组的最大和。
若dp[i-1]>0,dp[i] = dp[i-1]+nums[i]。
若dp[i-1]<=0, dp[i] = nums[i],因为一个数加上一个负数一定会比这个数本身小,若是前一个数是负数,则可以遗弃它,直接从当前元素开始找。
用res记录最大值可以避免之后在遍历一遍dp数组。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
int res = nums[0];
vector<int> dp(n, 0);
dp[0] = nums[0];
for(int i = 1; i < n; i++){
dp[i] = dp[i-1]>0 ? dp[i-1]+nums[i] : nums[i];
res = max(res, dp[i]);
}
return res;
}
};
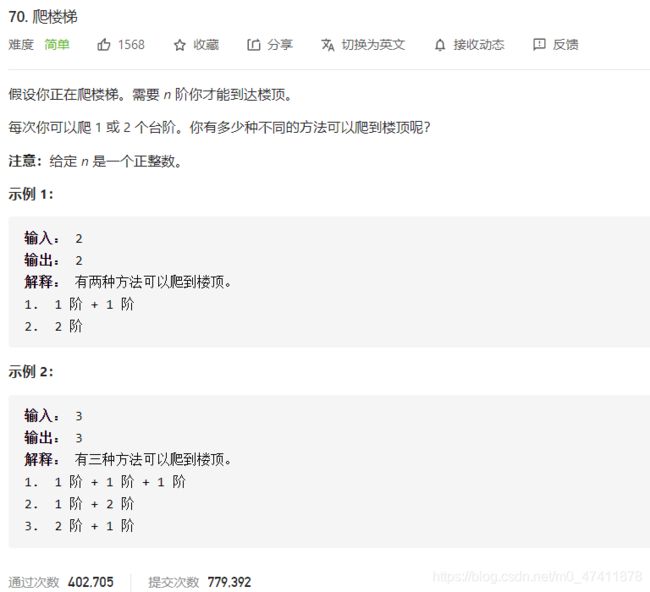
3.70–爬楼梯
(2)题解:
动态规划(简化)
题目条件是每次只能爬1个或2个台阶,所以要求爬到第n阶台阶的方法数时,该方法数等于爬到n-1阶台阶的方法数+爬到n-2阶台阶的方法数之和,状态转移方程是dp[n]=dp[n-1]+dp[n-2],由于只与前两个状态有关,所以没必要建立数组。
class Solution {
public:
int climbStairs(int n) {
if(n==0||n==1) return 1;
int x = 1, y = 1, sum;
for(int i = 2; i <= n; i++){
sum = x + y;
x = y;
y = sum;
}
return sum;
}
};
4.413–等差数列划分
(2)题解:
动态规划
dp[i]是以第i个元素结尾的等差数列的个数,由于求的是所有子数组的个数和,最后要把dp数组的元素个数相加。
等差数列的划分满足nums[i]-nums[i-1]=nums[i-1]-nums[i-2]
class Solution {
public:
int numberOfArithmeticSlices(vector<int>& nums) {
int n = nums.size();
if(n < 3) return 0;
vector<int> dp(n, 0);
for(int i = 2; i < n; i++){
if(nums[i]-nums[i-1] == nums[i-1]-nums[i-2]){
dp[i] = dp[i-1] + 1;
}
}
return accumulate(dp.begin(), dp.end(), 0);
}
};
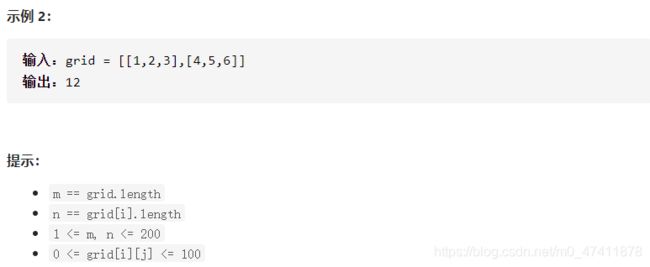
5.64–最小路径和
(2)题解:
动态规划(二维)
由题目条件可知,元素只能向右或者向下走,dp[i][j]代表以第i行第j列为结尾的元素的最小路径和,状态转移方程:
dp[i][j] = min(dp[i-1][j],dp[i][j-1])+grid[i][j]
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<vector<int>>dp(m, vector<int>(n,0));
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(i == 0 && j == 0){
dp[i][j] = grid[0][0];
}
else if(i == 0){
dp[i][j] = dp[i][j-1] + grid[i][j];
}
else if(j == 0){
dp[i][j] = dp[i-1][j] + grid[i][j];
}
else{
dp[i][j] = min(dp[i][j-1], dp[i-1][j]) + grid[i][j];
}
}
}
return dp[m-1][n-1];
}
};
动态规划压缩矩阵
由于dp数组遍历时只与左边和上边的值有关,我们可以将二维数组压缩成一维数组dp[j]代表遍历到第i行时,以第j列的元素结尾的最小路径和。
对于第i行,在遍历到第j列时,由于第j-1列已经遍历完,所以dp[j-1]代表dp[i][j-1],而dp[j]还没有被更新,所以dp[j]代表dp[i-1][j]
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<int> dp(n, 0);
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(i == 0 && j == 0){
dp[j] = grid[i][j];
}
else if(i == 0){
dp[j] = dp[j-1] + grid[i][j];
}
else if(j == 0){
dp[j] = dp[j] + grid[i][j];
}
else{
dp[j] = min(dp[j], dp[j-1]) + grid[i][j];
}
}
}
return dp[n-1];
}
};
6. 542–01矩阵
(2)题解:
广度优先搜索
bfs更为常见,这里只介绍动态规划方法
动态规划
对于矩阵中的1,要找到与它距离最近的0,共有四种走法:
水平向左+竖直向上
水平向左+竖直向下
水平向右+竖直向上
水平向右+竖直向下
可以四种情况都考虑,但是会有重复,所以为了减少重复次数,只选择左上和右下就可以,说明原因:
左上,从第一个元素开始遍历,对于每个元素都找到了左边和上边的最小值
右下,从最后一个元素开始遍历,对于每个元素都找到了右边和下边的最小值
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
//初始dp的值为无穷大
vector<vector<int>> dp(m, vector<int>(n, INT_MAX/2));
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(matrix[i][j] == 0){
dp[i][j] = 0;
}
}
}
//向左和向上,注意遍历顺序
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(i-1 >= 0)
dp[i][j] = min(dp[i][j], dp[i-1][j]+1);
if(j-1 >= 0)
dp[i][j] = min(dp[i][j], dp[i][j-1]+1);
}
}
//向右和向下,注意遍历顺序
for(int i = m-1; i >= 0; i--){
for(int j = n-1; j >= 0; j--){
if(i+1 < m)
dp[i][j] = min(dp[i][j], dp[i+1][j]+1);
if(j+1 < n)
dp[i][j] = min(dp[i][j], dp[i][j+1]+1);
}
}
return dp;
}
};
7.221-最大正方形
(2)题解:
动态规划
数组dp(i,j)表示以(i,j) 为右下角,且只包含 1 的正方形的边长最大值.
若matrix(i,j)=‘0’,dp(i,j)=0
若matrix(i,j)=‘1’,考虑边界条件,若i=0或者j=0,则dp(i,j)只能为1,若不是在边界,则满足状态转移方程dp(i,j)=min(dp(i-1,j),dp(i,j-1),dp(i-1,j-1))+1
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
int maxside = 0;
vector<vector<int>> dp(m, vector<int>(n, 0));
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(matrix[i][j] == '1'){
if(i == 0 || j == 0) dp[i][j] = 1;
else{
dp[i][j] = min(min(dp[i-1][j],dp[i-1][j-1]),dp[i][j-1])+1;
}
}
maxside = max(maxside, dp[i][j]);
}
}
return maxside*maxside;
}
};
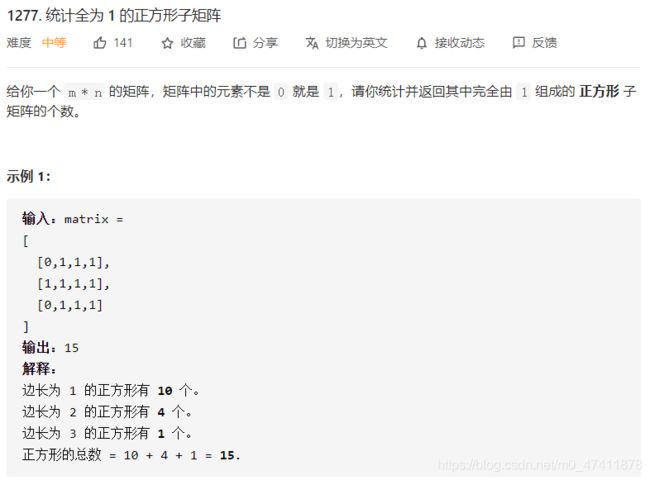
8.1277-统计全为1的正方形子矩阵
动态规划
这道题与221最大正方形十分类似,对dp(i,j)可以有不同的定义,定义为以(i,j)元素结尾的全1矩阵的个数,计算过程中用sum进行相加得到最终个数。
class Solution {
public:
int countSquares(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
int sum = 0;
vector<vector<int>> dp(m, vector<int>(n, 0));
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(matrix[i][j] == 1){
if(i == 0 || j == 0) dp[i][j] = 1;
else{
dp[i][j] = min(min(dp[i-1][j], dp[i-1][j-1]), dp[i][j-1]) + 1;
}
}
sum += dp[i][j];
}
}
return sum;
}
};