Pytorch笔记之回归

---

前言

以线性回归为例，记录Pytorch的基本使用方法。

---

一、导入库

import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.autograd import Variable # 定义求导变量
from torch import nn, optim # 定义网络模型和优化器

二、数据处理

将数据类型转为tensor，第一维度变为batch_size

# 构建数据
x = np.random.rand(100)
noise = np.random.normal(0, 0.01, x.shape)
y = 0.1 * x + 0.2 + noise
# 数据处理
x_data = torch.FloatTensor(x.reshape(-1, 1))
y_data = torch.FloatTensor(y.reshape(-1, 1))
inputs = Variable(x_data)
target = Variable(y_data)

三、构建模型

1、继承nn.Module，定义一个线性回归模型。在__init__中定义连接层，定义前向传播的方法
2、实例化模型，定义损失函数与优化器

# 继承模型
class LinearRegression(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc = nn.Linear(1, 1)
    def forward(self, x):
        out = self.fc(x)
        return out
# 定义模型
print('模型参数')
model = LinearRegression()
mse_loss = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
for name, param in model.named_parameters():
    print('{}:{}'.format(name, param))

四、迭代训练

1、梯度清零：optimizer.zero_grad()
2、反向传播计算梯度值：loss.backward()
3、执行参数更新：optimizer.step()
循环迭代，定期输出损失值

print('损失值')
for i in range(1001):
    out = model.forward(inputs)
    loss = mse_loss(out, target)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if i % 200 == 0:
        print(i, loss.item())

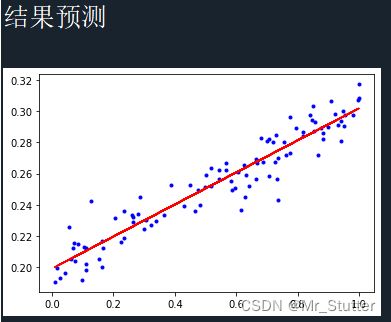
五、结果预测

绘制样本的散点图与预测值的折线图

print('结果预测')
y_pred = model(x_data)
plt.plot(x, y, 'b.')
plt.plot(x, y_pred.data.numpy(), 'r-')
plt.show()

---

总结

使用Pytorch进行训练主要的三步：
（1）数据处理：将数据维度转换为(batch, *)，数据类型转换为可训练的tensor;
（2）构建模型：继承nn.Module，定义连接层与运算方法，实例化，定义损失函数与优化器；
（3）迭代训练：循环迭代，依次执行梯度清零、梯度计算、参数更新。