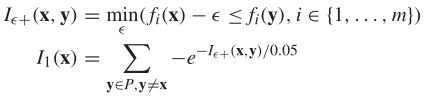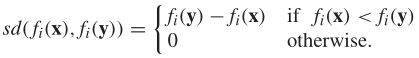SRA:基于多指标的多目标优化随机排序算法

SRA:基于多指标的多目标优化随机排序算法

参考文献
《Bingdong Li, Student Member , IEEE, Ke Tang, Senior Member , IEEE, Jinlong Li, Member , IEEE, and Xin Yao , Fellow, IEEE：Stochastic Ranking Algorithm for Many-Objective Optimization Based on Multiple Indicators》

要点

单一指标可能会有偏差，导致种群向帕累托前沿的一个次优区域汇聚。本文针对多目标优化问题，提出了一种基于多指标的算法。该算法采用随机排序技术来平衡不同指标的搜索偏差，即基于随机排序的多指标算法。

实证研究表明，与最先进的算法相比，SRA在反向世代距离和超体积指标方面表现良好。在一个问题需要算法具有很强的收敛能力的情况下，SRA的性能可以通过基于导向的档案来存储收敛良好的解和保持多样性来进一步提高。

一、介绍

随着多目标问题中目标数量的增加，非支配解的比例相当大，传统的帕累托支配失去了将种群推向最优解的效率。当基于支配的(主要)选择标准不能区分非支配解时，基于多样性的(次要)标准在环境选择中起着至关重要的作用。因此，最终的群体可能遍布整个目标空间，但无法收敛到PF。

为了克服这一障碍，研究者提出了各种多目标进化算法。根据所使用的关键思想，这些方法可以分为六类。

1）基于松弛支配的算法试图通过扩大解的支配区域来缓解支配的低效性。已经提出了一系列方法，例如ε-支配，控制解的支配面积，和L-支配。在这些松弛的定义下，一个解被其他解支配的机会更大，对PF的选择压力增加。一种代表性的基于支配的松弛算法是GrEA，它使用基于网格的收敛和多样性测量来比较非支配解。这些方法的一个难题在于确定不同问题的新支配定义的松弛程度，并且已经研究了动态调整方法。

2）基于多样性的方法试图通过更先进的多样性保持策略来提高性能。一般来说，这些方法通过考虑收敛到一定程度，减少多样性维护对选择压力的不利影响。

3）基于聚集的方法使用一系列的标量化函数来将多目标规划分解成一组单目标子问题。

4）基于指标的方法在优化MaOP时利用指标值来指导搜索过程。最终的解集主要取决于所包含的指标特征。然而，与其他算法相比，基于超体积的算法通常更耗时。评估GD和IGD值需要一个参考集作为PF。因为真正的PF通常是未知的，所以维护参考集也是一项非常重要的任务。

5）基于偏好的算法根据用户的偏好信息关注感兴趣的区域。为了选择解，文献中研究了一系列偏好模型，如目标指定、偏好多面体、目标加权等，然而如何选择合适的偏好模型可能是一个依赖于问题的任务。一种有趣的算法，即偏好启发的协同进化算法，将偏好信息建模为一组与种群共同进化的解。

6）最近，还提出了将两种或多种上述技术相结合的混合MaOEAs。两个有代表性的算法是NSGA-ⅲ和Two_Arch2。

本文采用随机排序技术，该技术最初是为了平衡约束优化中的适应度和约束违反而设计的。引入了一种新的技术来平衡多目标优化算法中不同指标的影响。这种平衡是通过基于随机冒泡排序过程来实现的。通过可调参数，使算法设计者能够在不同的指标之间进行适当的权衡。为了处理要求算法具有强收敛能力的问题，基于导向的档案（DBA）被结合到SRA中，以存储良好收敛的解并保持多样性。

二、拟议的SRA

A、概述

算法1描述了SRA的框架

B、指标

在计算上，算法1可以适应任何可计算的指标。然而，我们期望通过涉及两个指标来获得额外的好处，直观地说，它们应该显示不同的偏差，例如，一个倾向于趋同，另一个倾向于多元化。于是，指标Iε+和ISDE被用于SRA，因为这两个指标已被证明在趋同或多样性方面是有效的，它们不涉及设定适当的参考集/点这一重要任务。

加性指标Iε+和相应的I1(x)定义为

指标ISDE和相应的I2(x)定义为

其中

C、基于随机排序的环境选择

在多个指标的情况下，排序变得复杂得多，因为不同的指标可能会给同一个个体分配不同的等级。特别是当指标支持多目标优化的不同方面，即收敛性和多样性，这很可能发生。这种情况下的排序结果应该代表对同一种群产生不一致排序的两个指标之间的良好平衡。这种情况类似于约束(单目标)优化中通常遇到的情况，在这种情况下，通过根据适应度和约束违反对种群进行排序，可能会得到不同的结果。因此，SRA利用随机排序技术，一种已被证明对约束优化中的排序问题有效的方法，来解决多指标多目标优化中的排序问题。

具体来说，一旦获得所有个体的指标值，就应用随机排序。如算法2所示，随机排序是一种随机冒泡排序算法。

三、带存档的SRA

通过在SRA加入基于导向的档案DBA，产生了SRA的一种变体，即带档案的SRA(SRA2)。这里，搜索方向由一组权重向量定义，权重向量根据《K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints,” IEEE Trans. Evol. Comput., vol. 18, no. 4, pp. 577–601, Aug. 2014.》中的方法设置。给定一组权重向量，SRA2首先生成2N个个体，其中N个被随机分配给每个权重向量，并被视为初始档案。其余N个个体作为初始种群。在每一代中，档案中的每个成员都与从当前群体中随机选择的一个个体进行重组，以产生后代。然后，在环境选择步骤之后，使用新的群体更新档案。

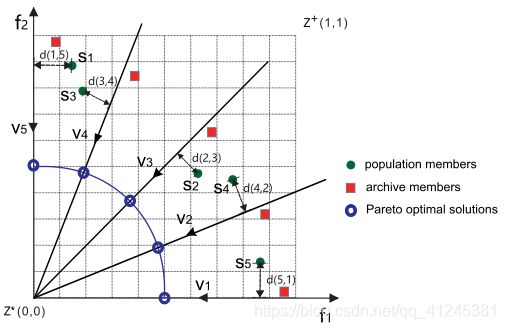
算法3中显示了档案更新过程的伪代码。对基于权重向量的方法，两个关键步骤是是关联和替换。在SRA2中，根据《K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints,” IEEE Trans. Evol. Comput., vol. 18, no. 4, pp. 577–601, Aug. 2014.》和《Y . Yuan, H. Xu, B. Wang, B. Zhang, and X. Y ao, “Balancing convergence and diversity in decomposition-based many-objective optimizers,” IEEE Trans. Evol. Comput., vol. 20, no. 2, pp. 180–198, Apr. 2016.》，个体与具有最小垂直距离的权重向量相关联。下图示出了关联步骤的图示。此后，个体最多可以替换对应于关联权重向量的邻域的nr个档案成员，只要其获得比沿着方向的档案成员更好的适应度值。基于惩罚的边界相交(PBI)适应度函数，定义为垂直距离和投影长度的加权和，在SRA2中用于比较个体和档案成员。