pytorch_神经网络构建3
文章目录
-
- 卷积神经网络
- 实现卷积层,池化层
- 池化层:
- 数据标准化
- AlexNet卷积网络
- 深层网络结构vgg
- googleNet网络结构
- ResNet网络结构
- DensNet网络结构
- 训练卷积神经网络会遇到的一些问题
- 学习率衰减
卷积神经网络
前面讲述了逻辑回归分类,模拟函数回归问题,单层,深层网络,它们以点和向量为代表,接下来讲述如何识别一张图片,
假设一张图片大小为1000x1000,rgb图像,我们应该如何对它识别分类

我们可以像处理手写数字识别一样把图片展开成一行,然后对每个数据参数求权重,然而实际操作确是极其不现实的,也是不合理的
因为仅仅输入就有300万参数,如果我们希望第一层拥有1000个神经元来对他进行输入,那么参数量将会是310^9
如果图像大小为1000010000那么处理一张图片的参数量将会十分巨大
传统意义上处理图片,有缩放,模糊,锐化等操作,可以在一定程度上降低图像质量和大小,但是不影响照片整体的判断
对图片的某个区域进行筛选出特征值,进行缩放是传统处理图像的技巧
受此启发,于是有人提出了滑动窗口的概念,我们不必把图片看做一个整体,而是让神经网络从局部窗口一个个观察它的特征,比如看看猫的耳朵,看看猫的眼睛,最后综合起来,也许不同的窗口学习了图像不同的特征,最后我们用这些特征来评价一张图片,这个滑动窗口,叫做卷积核
它在图片上滑动的过程中,与图片上对应的区域做卷积运算,最后我们训练的参数不再是图片上的每个像素点的权重,而是滑动窗口的权重
卷积核的大小,叫做ksize,在图片上移动的步长叫做stride,如果在图片移动过程中图片大小无法满足卷积核的运算要求,往往还会在原图象上补0以让卷积核进行扫描,这个操作称为padding
经过卷积核ksize和stride扫描后新图像的形状可以由以下公式得出
w为输入图像宽高,卷积核大小为k,填充大小为p,滑动步长为s
![]()
每个卷积核就像我们之前进行神经网络训练时的神经元一样,只不过不再是单独的一个w,而是一组w
如下图
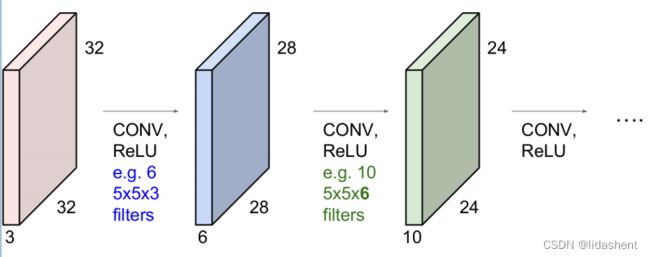
输入层–>卷积层–>池化层–>卷积层–>池化层–>全连接层–>全连接层–>全连接层
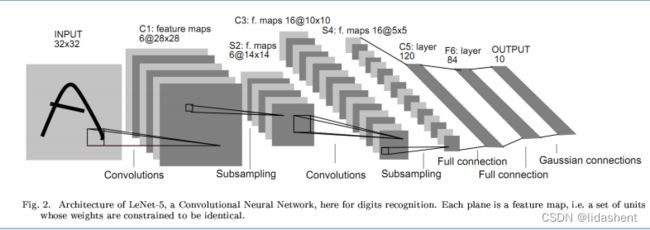
卷积层很好理解
图像经过每个卷积核后都会生成新的图像,如图32x32x3图像经过5x5x3的卷积运算扫描后得到28x28的一维图像
如果我们有6个卷积核,那么经过第一个卷积层后我们能够得到6个28X28图像,这和以往神经网络对矩阵的运算结果特征十分相似
那么可以说卷积核和他所输出的新图层构成了一个卷积层
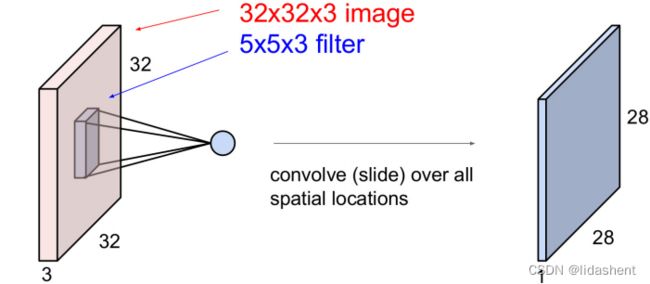
当然,卷积层也需要激活函数,对于不必要的特征有时会让relu替我们丢弃
池化层:
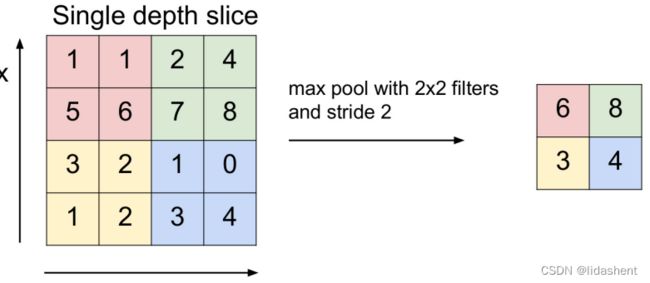
作用是对图像大小进行缩放,进行下采样操作,可以迅速降低图像大小而保留图像特征
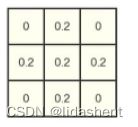
比如最大池化层max pooling(输出滑动窗口扫描区域的最大值),平均池化层average pooling(输出滑动窗口扫描区域的平均值)
如图,进行快速缩放,最大池化
全连接层:
将图片进行卷积操作后,图像的数据量已经急剧减小,将每张图片摊平成一行,可以为每个筛选下来的图像数据设置权重了
已经可以使用wx进行简单的运算了
至此,卷积神经网络,也被称为cnn,Convolutional Neural Network
实现卷积层,池化层
卷积层:
卷积层重要的是卷积核,需要设置卷积核的大小,扫描步长,以及卷积核的权重
幸运的是pytroch提供了两个函数来实现它,torch.nn.Conv2d(), torch.nn.functional.conv2d()
两者实现的结果是一样的,只是在应用时设置权重的方式不同
torch.nn.Conv2d()不用特意设置权重,设置好卷积核后会自动随机初始化权重,当然也可以指定权重
torch.nn.functional.conv2d()必须为其设定权重才会进行卷积操作
前者用的更多,无论训练和调试都可以胜任
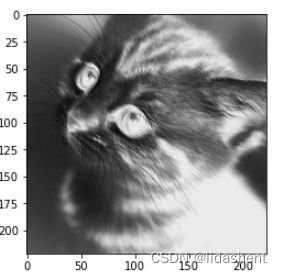
我们用灰度图读取一张图片,查看一下使用conv2d的效果
原始图片![]()
会得到原始图片的宽高,和灰度图
im=Image.open('./cat.png').convert('L')
im=np.array(im,dtype='float32')
plt.imshow(im.astype('uint8'),cmap='gray')
im.shape

接下来随机初始化权重,进行特征提取,我们只需要指定卷积核大小和步长即可
不过,为了进行卷积运算,需要对输入数据进行一次reshape[1,1,224,224]
代表batch size为1,channel为1,height为224,width为224,这是因为pytroch的计算数据格式为NCHW
卷积操作参数为(输入通道数1,输出通道数1,卷积核大小3X3,不设置偏置窗口)
修改卷积核大小可以使用参数(输入通道数1,输出通道数1,kernel_size=(4, 3),不设置偏置窗口)
queeze用来压缩张量,将维度为1的去除,这样就将[1,1,224,224]变为[224,224]的numpy图像矩阵
im=torch.from_numpy(im.reshape((1,1,im.shape[0],im.shape[1])))
conv1=nn.Conv2d(1,1,3,bias=False)
edge1=conv1(Variable(im))
print(conv1.weight.data)
edge1=edge1.data.squeeze().numpy()
plt.imshow(edge1,cmap='gray')
sobel_kernel=np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]],dtype='float32')
sobel_kernel=sobel_kernel.reshape((1,1,3,3))
weight=torch.from_numpy(sobel_kernel)
conv1.weight.data=weight
edge1=conv1(im)
print(conv1.weight.data)
edge1=edge1.data.squeeze().numpy()
plt.imshow(edge1,cmap='gray')
edge2=F.conv2d(im,weight)
edge2=edge2.data.squeeze().numpy()
plt.imshow(edge2,cmap='gray')
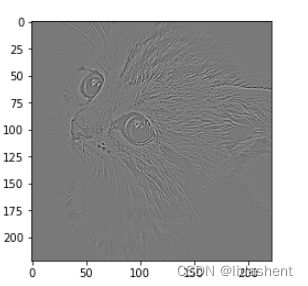
结果是一样的,所以torch.nn.functional.conv2d()并不常用
池化层:
受到传统图像处理的启发,我们可以缩小图像而不影响图像的判别
池化层没有参数,对于图像的处理有最大值池化,均值池化
设置滑动窗口的大小为2x2,步长为2,相比于卷积层他没有卷积计算操作
卷积核大小设置和卷积层一致
pool1=nn.MaxPool2d(2,2)
small_im=pool1(im)
print(small_im.shape)
small_im=small_im.data.squeeze().numpy()
plt.imshow(small_im,cmap='gray')
small_im=F.max_pool2d(im,2,2)
small_im=small_im.data.squeeze().numpy()
plt.imshow(small)
同样F.max_pool2d也不常用
到这里常用的卷积层和池化层,以及如何使用卷积和池化层就介绍完了
接下来我们关心的是网络结构的设计问题
但是在此之前,我们需要解决一个迫在眉睫的问题,对于大量数据的输入,我们该如何规范化这些数据,如果没有标准的数据输入,网络结构设计的再好,也很难得到一个好结果
数据标准化
数据预处理:
我们希望所有的数据是规范的,特征分布规模是适当的,
为了某种适当,我们希望数据分布在坐标原点周围来观察规律,可以使用0点中心化方法
每个特征维度都减去均值,最后我们会得到一个0均值分布
进一步,在0均值处理之后,我们可以将其除以标准差(平方差后求根)得到一个近似标准正态分布
更进一步 ,可以根据最大最小值,将其分布控制在(-1,1)区间

然而在实际训练中,尽管第一层输入时特征不相关,近似正态分布输入,但是由于神经网络的非线性特点,最后输出的结果会极大概率偏离N(0,1)正态分布,这让深度网络的构建困难重重
后来有人提出了一个新方法,批标准化来解决这个问题
那就是对每一层网络层输出都进行归一化,使其符合正态分布,
对一个训练批次的数据{x1,x2…}处理如下
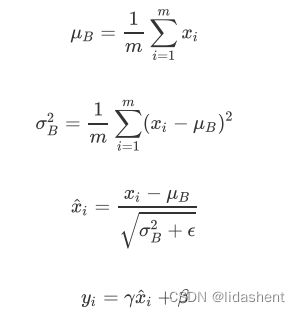
第一行和第二行很容易理解,就是求一个batch中的均值和方差,
第三个公式则根据方差对batch中的每个数据做标准化,为了防止底数为0,加了一个e,一般取e=10^-5
最后修正权重得到输出
那么接下来我们构建一个卷积神经网络,比如一个对图像分类的经典网络
AlexNet卷积网络
这个卷积网络当初是在一个图像分类比赛上取得了第一的成绩,如今我们对其进行实践一下
首先我们先下载图像数据集,将False改为True
classes = ('plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
train_set=CIFAR10('./data',train=True,download=False)
test_set=CIFAR10('./data',train=False,download=False)
im,label=test_set[0]
可以通过图像和标签查看其单个数据
![]()
cat
那么卷积网络除了创新性的提出了卷积核和池化层外其他训练方式和之前的分类网络并无不同
我们接下来需要设置神经网络结构,loss函数,参数优化器,输入数据标准化
它的网络结构为
卷积层1(3,64,5)(代表输入量3图,输出64图,5x5卷积核),relu激活层,最大池化层(3,2)(3x3池化,步长为2),卷积层2(64,64,5,1),relu激活层,最大池化层(3,2),全连接层(1024,384),全连接层(384,192),全连接层(192,10)
class AlexNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1=nn.Sequential(
nn.Conv2d(3,64,5),
nn.ReLU(True)
)
self.max_pool1=nn.MaxPool2d(3,2)
self.conv2=nn.Sequential(
nn.Conv2d(64,64,5,1),
nn.ReLU(True)
)
self.max_pool2=nn.MaxPool2d(3,2)
self.fc1=nn.Sequential(
nn.Linear(1024,384),
nn.ReLU(True)
)
self.fc2=nn.Sequential(
nn.Linear(384,192),
nn.ReLU(True)
)
self.fc3=nn.Linear(192,10)
def forward(self,x):
x=self.conv1(x)
x=self.max_pool1(x)
x=self.conv2(x)
x=self.max_pool2(x)
x=x.view(x.shape[0],-1)
x=self.fc1(x)
x=self.fc2(x)
x=self.fc3(x)
return x
alexnet=AlexNet()
定义loss函数,参数优化器,设置网络在GPU上进行训练
net=AlexNet().cuda()
optimizer=torch.optim.SGD(net.parameters(),lr=1e-1)
lossor=nn.CrossEntropyLoss()
为输入的数据进行标准化
x = x.transpose((2, 0, 1))
pytorch使用的数据格式为NCHW,即图片批次数量,通道数,高,宽
输入数据原本格式为HWC,比如1282563,需要交换通道到pytorch格式
from utils import train
def data_tf(x):
x=np.array(x,dtype='float32')/255
x=(x-0.5)/0.5
x=x.transpose((2,0,1))
x=torch.from_numpy(x)
return x
train_set=CIFAR10('./data',train=True,transform=data_tf)
test_set=CIFAR10('./data',train=False,transform=data_tf)
train_data=torch.utils.data.DataLoader(train_set,batch_size=64,shuffle=True)
test_data=torch.utils.data.DataLoader(test_set,batch_size=128,shuffle=True)
训练同以往一样,从数据迭代器中将数据输入神经网络,得到预测值,根据loss函数算出loss值
参数优化器清空梯度,loss进行反向传播,参数优化器更新参数,继续迭代
进行20次迭代,伪代码为
train(net,train_data,test_data,20,optimizer,lossor)
实际训练得到

20次迭代在测试集上就得到了71%的正确率,已经很不错了
深层网络结构vgg
思路是使用小的33卷积核堆叠和22的池化层,不仅能够减少参数,还能来加深神经网络结构,试图构建真正意义上的深层网络结构
它在2014年夺得了imageNet的第二名,那么第一名是谁呢?比vgg厉害,不过vgg的思路也是第一名的思路,只不过第一名做了比vgg更多的开创性工作
它的网络深度十分复杂,但是构造十分简单,但是为后来更深层次的神经网络提供了很好的借鉴意义
它包含输入层,隐含层,全连接层,输出层,隐含层使用了大量的重复结构块
结构块函数:
设置生成一些重复的网络结构,参数(生成N个卷积层,输入通道数,输出通道数)
因为最后使用了(2,2)池化,最后输出的图像大小为原图的一半
def vgg_block(num_convs, in_channels, out_channels):
net = [nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1), nn.ReLU(True)] # 定义第一层
for i in range(num_convs-1): # 定义后面的很多层
net.append(nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1))
net.append(nn.ReLU(True))
net.append(nn.MaxPool2d(2, 2)) # 定义池化层
return nn.Sequential(*net)
结构块堆叠函数:
用于构建不同的结构块,将它们堆叠起来构成复杂的隐含层
参数(卷积层数列表,通道数目列表)
将根据卷积层数列表,生成对应层数的n个卷积层,其中每个卷积层的输入和输出由对应的通道列表值控制
def vgg_stack(num_convs, channels):
net = []
for n, c in zip(num_convs, channels):
in_c = c[0]
out_c = c[1]
net.append(vgg_block(n, in_c, out_c))
return nn.Sequential(*net)
如图,构建如下隐含层:
vgg_net = vgg_stack((1, 1, 2, 2, 2), ((3, 64), (64, 128), (128, 256), (256, 512), (512, 512)))
print(vgg_net)
将会生成5个网络结构,每个结构对前一个图像减小1/2,其中第一个网络结构为1个3通道输入,64通道输出的卷积层
第二个网络结构为1个64通道输入,128通道输出的卷积层
第三个网络结构为2个128通道输入,256通道输出的卷积层…
举个例子:
testX=torch.zeros(1,3,256,256)
testY=vgg_net(testX)
print(testY.shape)
最后结果为torch.Size([1, 512, 8, 8]),图像大小由256x256降低到8*8,2^5,因为一共有5个2x2池化层对其进行缩小
分别图像降维为128-64-32-16-8
最后,我们为这个深度结构加上全连接层10分类作为输出,vggNet就算构建完成了
class vgg(nn.Module):
def __init__(self):
super(vgg,self).__init__()
self.feature=vgg_net
self.fc=nn.Sequential(
nn.Linear(512,100),
nn.ReLU(True),
nn.Linear(100,10)
)
def forward(self,x):
x=self.feature(x)
x=x.view(x.shape[0],-1)
x=self.fc(x)
return x
测试一下效果
vggNet=vgg()
optimizer=torch.optim.SGD(vggNet.parameters(),lr=1e-1)
lossor=nn.CrossEntropyLoss()
# print(vggNet)
train(vggNet,train_data,test_data,20,optimizer,lossor)

20次迭代正确率达到了77%,看来更深层次的网络和小的卷积核对神经网络的优化效果十分显著
googleNet网络结构
前面讲述了2014年ImagNet第二名的网络结构,那么来看看第一名的
两者同样意识到了深度网络带来的巨大潜力,只不过第一比第二创新性的提出了一个 inception 模块
这个模块的核心思想是在原图大小不变的情况下,增加图形的通道维度数量

原图经过6个卷积核,1次池化,共四类操作处理后进行拼接进行通道维度扩容
比如39696扩充到2569696,同时在每个卷积层输出的数据后进行数据正态分布标准化,让输出数据分布符合正态分布
单看为每个卷积层所做的工作:
设置输入通道数,输出通道数,卷积核大小,步长,填充
输出结果进行正态分布标准化,又称为批量归一化,eps是为了计算正态分布时防止分母为0
再加一个激活函数,构成了inception模块的卷积块
def conv_relu(in_channel, out_channel, kernel, stride=1, padding=0):
layer = nn.Sequential(
nn.Conv2d(in_channel, out_channel, kernel, stride, padding),
nn.BatchNorm2d(out_channel, eps=1e-3),
nn.ReLU(True)
)
return layer
基于此,我们构建如上图的一个inception模块
class inception(nn.Module):
def __init__(self, in_channel, out1_1, out2_1, out2_3, out3_1, out3_5, out4_1):
super(inception, self).__init__()
# 第一条线路
self.branch1x1 = conv_relu(in_channel, out1_1, 1)
# 第二条线路
self.branch3x3 = nn.Sequential(
conv_relu(in_channel, out2_1, 1),
conv_relu(out2_1, out2_3, 3, padding=1)
)
# 第三条线路
self.branch5x5 = nn.Sequential(
conv_relu(in_channel, out3_1, 1),
conv_relu(out3_1, out3_5, 5, padding=2)
)
# 第四条线路
self.branch_pool = nn.Sequential(
nn.MaxPool2d(3, stride=1, padding=1),
conv_relu(in_channel, out4_1, 1)
)
def forward(self, x):
# print(self.branch_pool)
f1 = self.branch1x1(x)
f2 = self.branch3x3(x)
f3 = self.branch5x5(x)
f4 = self.branch_pool(x)
print(f1.shape)
print(f2.shape)
print(f3.shape)
print(f4.shape)
output = torch.cat((f1, f2, f3, f4), dim=1)
return output
我们输入一张测试图,查看是否扩容成功
test_net = inception(3, 64, 48, 64, 64, 96, 32)
test_x = Variable(torch.zeros(1, 3, 96, 96))
print('input shape: {} x {} x {}'.format(test_x.shape[1], test_x.shape[2], test_x.shape[3]))
test_y = test_net(test_x)
print('output shape: {} x {} x {}'.format(test_y.shape[1], test_y.shape[2], test_y.shape[3]))
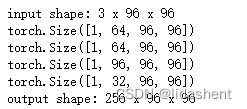
可以看到第一类操作扩容了64个通道,第二类操作扩容了64个通道,第三类操作扩容96个通道,第四类操作扩容了32个通道,最后将它们拼接在一起成为了一个具备256维度的96*96图像
那么,我们的每个图像都进行如此扩容,然后再放入网络结构中进行训练,就可以设计更加深度的网络
依旧是CIFAR10分类,我们为其设计googlnet网络结构
class googlenet(nn.Module):
def __init__(self, in_channel, num_classes, verbose=False):
super(googlenet, self).__init__()
self.verbose = verbose
self.block1 = nn.Sequential(
conv_relu(in_channel, out_channel=64, kernel=7, stride=2, padding=3),
nn.MaxPool2d(3, 2)
)
self.block2 = nn.Sequential(
conv_relu(64, 64, kernel=1),
conv_relu(64, 192, kernel=3, padding=1),
nn.MaxPool2d(3, 2)
)
self.block3 = nn.Sequential(
inception(192, 64, 96, 128, 16, 32, 32),
inception(256, 128, 128, 192, 32, 96, 64),
nn.MaxPool2d(3, 2)
)
self.block4 = nn.Sequential(
inception(480, 192, 96, 208, 16, 48, 64),
inception(512, 160, 112, 224, 24, 64, 64),
inception(512, 128, 128, 256, 24, 64, 64),
inception(512, 112, 144, 288, 32, 64, 64),
inception(528, 256, 160, 320, 32, 128, 128),
nn.MaxPool2d(3, 2)
)
self.block5 = nn.Sequential(
inception(832, 256, 160, 320, 32, 128, 128),
inception(832, 384, 182, 384, 48, 128, 128),
nn.AvgPool2d(2)
)
self.classifier = nn.Linear(1024, num_classes)
def forward(self, x):
x = self.block1(x)
if self.verbose:
print('block 1 output: {}'.format(x.shape))
x = self.block2(x)
if self.verbose:
print('block 2 output: {}'.format(x.shape))
x = self.block3(x)
if self.verbose:
print('block 3 output: {}'.format(x.shape))
x = self.block4(x)
if self.verbose:
print('block 4 output: {}'.format(x.shape))
x = self.block5(x)
if self.verbose:
print('block 5 output: {}'.format(x.shape))
x = x.view(x.shape[0], -1)
x = self.classifier(x)
return x
我们对这个网络的输出进行一次测试,查看其分类结果,这已经是一个具备深度结构的网络了
test_net = googlenet(3, 10,True)
test_x = Variable(torch.zeros(1, 3, 96, 96))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))

网络结构已经具备了,接下来为其设置loss函数,参数优化器,以及对输入数据进行标准化,即可展开训练了
然而因为CIFAR原图为28*28,可以适当对其进行放大
def data_tf(x):
x = x.resize((96, 96), 2) # 将图片放大到 96 x 96
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化
x = x.transpose((2, 0, 1))
x = torch.from_numpy(x)
return x
然后创建googlNet对象,查看20次训练效果
googleNet = googlenet(3, 10)
optimizer = torch.optim.SGD(googleNet.parameters(), lr=0.01)
losser = nn.CrossEntropyLoss()
train(googleNet, train_data, test_data, 20, optimizer, losser)

似乎和vggnet差别不大,但是训练多次后其准确率将超过vggnet,深层网络的拟合能力比浅层更强,似乎外国人比我们更早的意识到这一点,当他们愿意花十几亿美金只为了训练一个模型时,我们还在抱着单卡3060ti训练的小模型沾沾自喜,于是chatGPT出来时给大家的震撼程度无异于一颗重磅炸弹
ResNet网络结构
这个结构提出了一个(跨层链接)残差模块用于解决梯度回传消失的问题,类似大脑中的神经元链接不是一层层,而是网状结构,可能输入层直连输出层,输入层也可能直连任何一个中间层,当然这个现在连接还没有那么稠密,resNet仅仅做到了跨层连接,
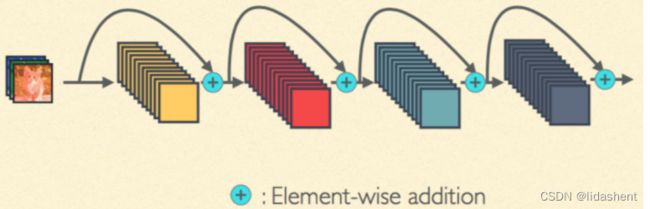
而真正的特征之间相互链接还需要下面的DenseNet实现
梯度回传消失的问题在深层网络中经常出现
由于反向传播的特性,使用链式法则,随着网络层数的增多,当导数小于1时,越靠近输入层导数越接近为0,导致参数迟迟无法更新
比如sigmoid函数
有时无法确定哪里出了问题,函数迟迟不能收敛,模型无法学习,需要解决梯度过小无法学习的问题
残差模块的思想是将之前的输入越过中间模块,直接传输到目标输出,然后再对中间模块进行更新参数优化,这样不会导致梯度过低无法更新参数的问题
举个最简单的例子是,输入x,目标h(x),正常应该是x-f(x)-h(x),一层层训练,但是我们直接把x传过去,变成x-(x+h(x)),然后不断优化f(x)接近H(x),
f(x)=h(x)-x
接下来先定一层卷积网络作为残差网络的基石,然后我们用True,False参数来控制一个网络块是否是残差模块,设计出一个三维网络
我们可以把之前一层层传递w的网络叫做二维网络,现在有了残差模块让层与层之间网络更短,我们将在神经网络上创建真正意义上第三个维度的参数
这一层主要用来控制卷积核步长,步长将会决定一个输入图是否是原样输出
def conv3x3(in_channel, out_channel, stride=1):
return nn.Conv2d(in_channel, out_channel, 3, stride=stride, padding=1, bias=False)
构建残差模块
当输入参数为True时,步长为1,输入将原样输出,为false时步长为2,输出将原图缩小为1/2
class residual_block(nn.Module):
def __init__(self, in_channel, out_channel, same_shape=True):
super(residual_block, self).__init__()
self.same_shape = same_shape
stride=1 if self.same_shape else 2
self.conv1 = conv3x3(in_channel, out_channel, stride=stride)
self.bn1 = nn.BatchNorm2d(out_channel)
self.conv2 = conv3x3(out_channel, out_channel)
self.bn2 = nn.BatchNorm2d(out_channel)
if not self.same_shape:
self.conv3 = nn.Conv2d(in_channel, out_channel, 1, stride=stride)
def forward(self, x):
out = self.conv1(x)
out = F.relu(self.bn1(out), True)
out = self.conv2(out)
out = F.relu(self.bn2(out), True)
if not self.same_shape:
x = self.conv3(x)
return F.relu(x+out, True)
会产生如下效果
设置为残差模块
# 输入输出形状相同
test_net = residual_block(32, 32)
test_x = Variable(torch.zeros(1, 32, 96, 96))
print('input: {}'.format(test_x.shape))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))
# 输入输出形状不同
test_net = residual_block(3, 32, False)
test_x = Variable(torch.zeros(1, 3, 96, 96))
print('input: {}'.format(test_x.shape))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))
class resnet(nn.Module):
def __init__(self, in_channel, num_classes, verbose=False):
super(resnet, self).__init__()
self.verbose = verbose
self.block1 = nn.Conv2d(in_channel, 64, 7, 2)
self.block2 = nn.Sequential(
nn.MaxPool2d(3, 2),
residual_block(64, 64),
residual_block(64, 64)
)
self.block3 = nn.Sequential(
residual_block(64, 128, False),
residual_block(128, 128)
)
self.block4 = nn.Sequential(
residual_block(128, 256, False),
residual_block(256, 256)
)
self.block5 = nn.Sequential(
residual_block(256, 512, False),
residual_block(512, 512),
nn.AvgPool2d(3)
)
self.classifier = nn.Linear(512, num_classes)
def forward(self, x):
x = self.block1(x)
if self.verbose:
print('block 1 output: {}'.format(x.shape))
x = self.block2(x)
if self.verbose:
print('block 2 output: {}'.format(x.shape))
x = self.block3(x)
if self.verbose:
print('block 3 output: {}'.format(x.shape))
x = self.block4(x)
if self.verbose:
print('block 4 output: {}'.format(x.shape))
x = self.block5(x)
if self.verbose:
print('block 5 output: {}'.format(x.shape))
x = x.view(x.shape[0], -1)
x = self.classifier(x)
return x
查看网络中每个模块输出之后的图层大小
test_net = resnet(3, 10, True)
test_x = Variable(torch.zeros(1, 3, 96, 96))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))
查看训练结果
resNet = resnet(3, 10)
optimizer = torch.optim.SGD(resNet.parameters(), lr=0.01)
criterion = nn.CrossEntropyLoss()
train(resNet, train_data, test_data, 20, optimizer, criterion)

20次的训练得到了80%正确率,已经领先许多简单的网络了,相比无残差模块的深层网络训练更快,效果也更好
DensNet网络结构

如图所示,拼接在通道维度上进行,底层的输出会传递到后面的所有层,低维的特征和高维的特征将会联合训练
接下来实践这个网络
定义网络块,它将作为denseNet网络的基石
对输入的数据标准化,然后创建一个relu激活函数,和一个卷积核对图像操作
def conv_block(in_channel, out_channel):
layer = nn.Sequential(
nn.BatchNorm2d(in_channel),
nn.ReLU(True),
nn.Conv2d(in_channel, out_channel, 3, padding=1, bias=False)
)
return layer
接下来,创建Dense块,它将所有层的数据持续向后传递,
class dense_block(nn.Module):
def __init__(self, in_channel, growth_rate, num_layers):
super(dense_block, self).__init__()
block = []
channel = in_channel
for i in range(num_layers):
block.append(conv_block(channel, growth_rate))
channel += growth_rate
self.net = nn.Sequential(*block)
def forward(self, x):
for layer in self.net:
out = layer(x)
x = torch.cat((out, x), dim=1)
return x
实践是否如此
test_net = dense_block(3, 12, 3)
test_x = Variable(torch.zeros(1, 3, 96, 96))
print('input shape: {} x {} x {}'.format(test_x.shape[1], test_x.shape[2], test_x.shape[3]))
test_y = test_net(test_x)
print('output shape: {} x {} x {}'.format(test_y.shape[1], test_y.shape[2], test_y.shape[3]))
![]()
但是存在一个问题,如果网络很深,通道维度持续累加,最后计算量越来越大,这对于构建超深度神经网络是不利的
因此,应该对每一层的输出进行降维,不至于让通道累加太快
denseNet引入了一个叫做过渡层的概念,使用1x1卷积核,但是最后要经过(2,2)池化,这会让图片宽高减半,同时可以更改通道数目
def transition(in_channel, out_channel):
trans_layer = nn.Sequential(
nn.BatchNorm2d(in_channel),
nn.ReLU(True),
nn.Conv2d(in_channel, out_channel, 1),
nn.AvgPool2d(2, 2)
)
return trans_layer
查看经过过滤后的图像效果
test_net = transition(3, 12)
test_x = Variable(torch.zeros(1, 3, 96, 96))
print('input shape: {} x {} x {}'.format(test_x.shape[1], test_x.shape[2], test_x.shape[3]))
test_y = test_net(test_x)
print('output shape: {} x {} x {}'.format(test_y.shape[1], test_y.shape[2], test_y.shape[3]))
通道数目和图像大小按照我们所要求的进行了变化
根据dense块构建denseNet网络
class densenet(nn.Module):
def __init__(self, in_channel, num_classes, growth_rate=32, block_layers=[6, 12, 24, 16]):
super(densenet, self).__init__()
self.block1 = nn.Sequential(
nn.Conv2d(in_channel, 64, 7, 2, 3),
nn.BatchNorm2d(64),
nn.ReLU(True),
nn.MaxPool2d(3, 2, padding=1)
)
channels = 64
block = []
for i, layers in enumerate(block_layers):
block.append(dense_block(channels, growth_rate, layers))
channels += layers * growth_rate
if i != len(block_layers) - 1:
block.append(transition(channels, channels // 2)) # 通过 transition 层将大小减半,通道数减半
channels = channels // 2
self.block2 = nn.Sequential(*block)
self.block2.add_module('bn', nn.BatchNorm2d(channels))
self.block2.add_module('relu', nn.ReLU(True))
self.block2.add_module('avg_pool', nn.AvgPool2d(3))
self.classifier = nn.Linear(channels, num_classes)
def forward(self, x):
x = self.block1(x)
x = self.block2(x)
x = x.view(x.shape[0], -1)
x = self.classifier(x)
return x
查看网络对入输入图像的输出
test_net = densenet(3, 10)
test_x = Variable(torch.zeros(1, 3, 96, 96))
test_y = test_net(test_x)
print('output: {}'.format(test_y.shape))
![]()
尝试训练网络
denseNet = densenet(3, 10)
optimizer = torch.optim.SGD(denseNet.parameters(), lr=0.01)
criterion = nn.CrossEntropyLoss()
train(denseNet, train_data, test_data, 20, optimizer, criterion)

可以看到经过20次训练,正确率还不稳定,但性能已经在测试集上已经有83%
denseNet为神经网络的构建奠定了坚实的基础,为后来的超规模搭建提供了很好的思路
训练卷积神经网络会遇到的一些问题
首先明白几个名词,
欠拟合:模型还没有训练到最优点,增加次数和改变网络结构都可以,表现为训练显示拉胯,测试拉胯
过拟合:模型在训练集上表现良好,在训练集上学习到了特殊的局部特征,表现为训练集表现良好,测试拉胯
改善过拟合现象一般的手法有,数据增强,dropout,正则化
数据增强:
对原始数据进行处理得到新的数据,一定程度上可以避免过拟合问题,这部分原因是数据量和特征不足造成的
1.缩放图片,2对图片随机截取3,对图片随机水平竖直翻转,4,对图片随机角度旋转,5,对图片亮度,对比度,颜色,随机变化
dropout:
受到人类大脑的启发,人脑在发育过程中对于一些不常用的神经元会关闭,建立新的连接
那么我们可以在训练时随机关闭一些神经元,看看不同的结构的输出,提高泛化能力
每个神经元被关闭的概率为p,那么x的期望为px,为了输出相同,往往还要计算1/p来得到x
pytroch中使用nn.Dropout§来表示
dropout一般用于全连接层,但是现在的卷积网络正在逐渐放弃使用全连接层,所以现在很少用dropout了
正则化:
机器学习提出的一种方法,有L1,L2正则化
常见的有L2正则化,它对loss函数进行了改进,加上了参数的二范数
二范数:也被称为L2范数,是向量中各元素的平方和的平方根,
比如![]()
常用它来防止过拟合,实际使用时对λ(权重筛选系数) 进行限制,太大会抑制参数更新,太小会导致贡献不大,常用为0.001
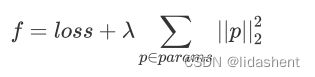
当我们对新的loss函数进行梯度下降,就会有

参数更新时就会有
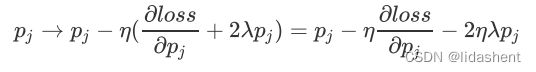
学习率衰减
学习率控制着梯度更新的步长,我们希望它能让loss下降到最低,当学习率为固定值后可能会在结果那里产生正确率震荡,无法进一步下降
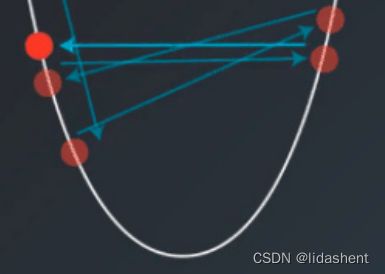
我们希望他能够随着训练的进行不断减小学习率来逼近loss最低点
迁移学习:
将已有的预训练模型放到我们自己的数据集上继续训练,可以根据我们的需要更新最后的全连接层
这对于小批次数据的训练是有利的
举个例子,我们要识别一辆车的图片,但是我们的数据量不足,而ImageNet上有众多的车的图片,我们当然可以使用它的图片来进行训练,但是我们也可以直接拿imageNet已经训练好的模型过来,最后我们更新全连接层,输出对车辆的识别即可