陀螺仪工作原理
陀螺仪,又叫角速度传感器,是用高速回转体的动量矩敏感壳体相对惯性空间绕正交于自转轴的一个或二个轴的角运动检测装置,同时,利用其他原理制成的角运动检测装置起同样功能的装置也称陀螺仪。陀螺仪的原理就是,一个旋转物体的旋转轴所指的方向在不受外力影响时,是不会改变的。
1、陀螺仪的名字由来
陀螺仪名字的来源具有悠久的历史。据考证,1850年法国的物理学家莱昂·傅科(J.Foucault)为了研究地球自转,首先发现高速转动中地的转子(rotor),由于它具有惯性,它的旋转轴永远指向一固定方向,因此傅科用希腊字 gyro(旋转)和skopein(看)两字合为“gyro scopei ”一字来命名该仪器仪表。
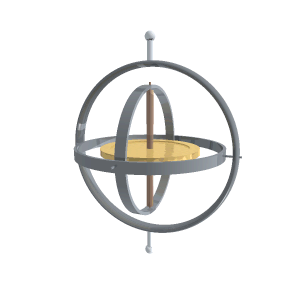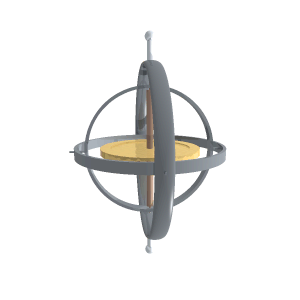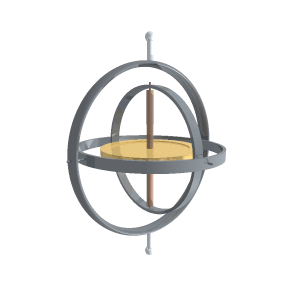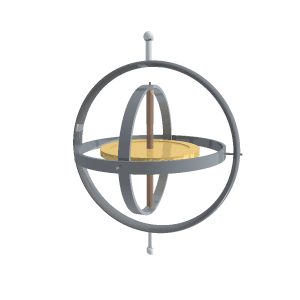
最早的陀螺仪的简易制作方式如下:即将一个高速旋转的陀螺放到一个万向支架上,靠陀螺的方向来计算角速度,简易图如下图所示。

其中,中间金色的转子即为陀螺,它因为惯性作用是不会受到影响的,周边的三个“钢圈”则会因为设备的改变姿态而跟着改变,通过这样来检测设备当前的状态,而这三个“钢圈”所在的轴,也就是三轴陀螺仪里面的“三轴”,即X轴、y轴、Z轴,三个轴围成的立体空间联合检测各种动作,然后用多种方法读取轴所指示的方向,并自动将数据信号传给控制系统。因此一开始,陀螺仪的最主要的作用在于可以测量角速度。
2、陀螺仪的基本组成
当前,从力学的观点近似的分析陀螺的运动时,可以把它看成是一个刚体,刚体上有一个万向支点,而陀螺可以绕着这个支点作三个自由度的转动,所以陀螺的运动是属于刚体绕一个定点的转动运动,更确切地说,一个绕对称轴高速旋转的飞轮转子叫陀螺。将陀螺安装在框架装置上,使陀螺的自转轴有角转动的自由度,这种装置的总体叫做陀螺仪。

- 陀螺转子(常采用同步电机、磁滞电机、三相交流电机等拖动方法来使陀螺转子绕自转轴高速旋转,并见其转速近似为常值)
- 内、外框架(或称内、外环,它是使陀螺自转轴获得所需角转动自由度的结构)
- 附件(是指力矩马达、信号传感器等)。
3、陀螺仪的工作原理
陀螺仪侦测的是角速度。其工作原理基于科里奥利力的原理:当一个物体在坐标系中直线移动时,假设坐标系做一个旋转,那么在旋转的过程中,物体会感受到一个垂直的力和垂直方向的加速度。
科里奥利力(Coriolis Effect)是由地球自转引起的一种惯性力。其效果主要体现在大气环流、海洋环流以及长程导弹飞行轨迹等方面。
其基础原理如下:在地球上,当一个物体进行运动时,由于地球的自转,物体运动轨迹会偏离其初衷的线性路径。这种现象被定义为科里奥利效应。
从具体角度来讲,由于地球上不同的纬度自转速度不同,当一个物体从高纬度向低纬度移动,由于高纬度地区地球自转速度较慢,而低纬度地区地球自转速度较快,所以物体运动中会出现一种向右偏的趋势(在北半球)。反之,如果物体从低纬度向高纬度移动,则由于低纬度地区自转速度较快,高纬度地区自转速度较慢,物体会出现一种向左偏的趋势。
具体到风的运动,气流会受到科里奥利力的影响显著地偏离其运动路径。这是由于科里奥利力在南北方向上的变化,使得风的运动方向发生改变。例如,在北半球,风会偏向右方;在南半球,风会偏向左方。这成为了风向循环模式的基础。
需要注意的是,科里奥利力不影响速度,只影响方向。在静止的参考系中看,速度和方向都可能改变,看起来就像受到了一个力的作用,这个力就是科里奥利力。
总的来说,科里奥利力并不是一种真正的物理力,而是由于我们在一个旋转的参考系(地球)内观察物体运动时产生的一个视觉效果。
4、陀螺仪的两大动力特性
陀螺仪被广泛用于航空、航天和航海领域。这是由于它的两个基本特性:一为定轴性(inertia or rigidity),另一是进动性(precession),这两种特性都是建立在牛顿的旋转运动第二定律和角动量守恒的原则下。
牛顿的旋转运动第二定律又被称为“力矩定律”,它描述的是物体在扭转力(也被称为力矩)作用下的旋转效果。
这一定律的内容是:物体的角加速度与作用在物体上的力矩成正比,并与物体的转动惯量成反比。可以被综合表述为“力矩等于转动惯量和角加速度的乘积”,数学形式为:
τ = I * α
其中, τ是力矩,I是物体的转动惯量,α是物体的角加速度。
这一定律与牛顿的线性运动第二定律(力等于质量和加速度的乘积,F=ma)类似,只是这里的力被替换为力矩,质量被替换为转动惯量,线性加速度被替换为角加速度。它们体现了力与运动之间的关系,是描述和分析物体运动的关键定律。
角动量守恒定律,也被称为转动动量守恒定律,是一个物理定律,用来描述在一个封闭系统中,无外力(或外力矩)作用下,系统的总角动量保持不变。
角动量守恒定律的表达式可写为: L = I * ω = constant
其中,L代表角动量,I是物体的转动惯量,也就是物体对于旋转的“惯性”,ω是物体的角速度。
该定律的应用非常广泛,包括天体运动、电子在原子内的运动、陀螺仪的运动等等。比如地球绕太阳运动时,因为太阳引力对地球的力矩为零,所以地球的轨道角动量是保持不变的。又比如在自行车、摩托车等车辆转弯时,车手往往会倾斜车身,而不是改变方向盘转向,这都是利用了角动量守恒定律。
我们首先考虑角动量守恒定律。在没有外力矩作用的情况下,陀螺仪的角动量是一个恒定的值,即L = Iω(L代表角动量,I代表转动惯量,ω代表角速度)。初始情况下,陀螺仪的旋转轴是垂直的,这也就意味着初始的角动量矢量也是垂直的。
当对陀螺仪施加外力时,例如向其斜侧施加力,这会产生一个力矩,而力矩的定义就是力和力臂(力的作用点到旋转轴的距离)的乘积。
根据牛顿第二定律的转动版,力矩等于角动量的变化速率,或者说力矩等于角动量的改变除以时间。但是,由于角动量守恒,陀螺仪的总角动量是不变的。在这种情况下,角动量的数量并未真实改变,而是改变了它的指向,形成了陀螺仪的“进动”。
这种力矩对角动量的改变形成陀螺仪的“定轴性”。也就是说,即使在外力矩的作用下,陀螺仪的旋转轴总是倾向于保持其原始的方向。这就是陀螺仪广泛应用于飞行器、导航系统、手机等方面的原因,它能保持或者测量一个特定的方向。
总的来说,陀螺仪的“定轴性”是由于角动量守恒的原理,即使受到外部力矩的作用,陀螺仪的总角动量也会保持恒定,使得旋转轴倾向于保持其原始的方向。
4.1 定轴性
当陀螺转子以高速旋转时,在没有任何外力矩作用在陀螺仪上时,陀螺仪的自转轴在惯性空间中的指向保持稳定不变,即指向一个固定的方向;同时反抗任何改变转子轴向的力量。这种物理现象称为陀螺仪的定轴性或稳定性。其稳定性随以下的物理量而改变:
- 转子的转动惯量愈大,稳定性愈好;
- 转子角速度愈大,稳定性愈好。
所谓的“转动惯量”,是描述刚体在转动中的惯性大小的物理量。当以相同的力矩分别作用于两个绕定轴转动的不同刚体时,它们所获得的角速度一般是不一样的,转动惯量大的刚体所获得的角速度小,也就是保持原有转动状态的惯性大;反之,转动惯量小的刚体所获得的角速度大,也就是保持原有转动状态的惯性小。
转动惯量(Moment of Inertia)是物理学中用来描述物体对旋转的"惯性"的一个标量。它用来描述物体抵抗角加速度改变的能力。在物体的质量分布均匀,且旋转轴穿过物体质心,物体形状规整的简单情况下,转动惯量的计算公式如下:
- 对于一根长度为L,质量为m的细长杆,如果绕过通过杆的一端且垂直于杆的轴旋转,转动惯量I=1/3mL²。
- 如果这根杆是绕过通过杆的中点且垂直于杆的轴旋转,则转动惯量I=1/12mL²。
- 对于一个半径为R,质量为m的圆盘,如果绕过通过圆心且垂直于圆盘的轴旋转,转动惯量I=1/2mR²。
- 在复杂的情况下,可以通过积分来计算转动惯量: I = ∫ r² dm 其中r是物体中每一个微小部分到旋转轴线的距离,dm是这个微小部分的质量,对整个物体进行积分求和就得到了物体关于该轴的转动惯量。
4.2 进动性
在对陀螺仪施加某种外加力矩时,陀螺仪的旋转轴并不会立即按照通常的力的作用方向转动,比如说直接倾倒。相反,由于角动量守恒的原理,它会倾向于保持其初始的旋转轴不变。然而,施加的力矩实际上改变了角动量的方向,从而引发了陀螺仪旋转轴的旋转,这个就是进动。
当转子高速旋转时,若外力矩作用于外环轴,陀螺仪将绕内环轴转动;若外力矩作用于内环轴,陀螺仪将绕外环轴转动。其转动角速度方向与外力矩作用方向互相垂直。这种特性,叫做陀螺仪的进动性。进动角速度的方向取决于动量矩H的方向(与转子自转角速度矢量的方向一致)和外力矩M的方向,而且是自转角速度矢量以最短的路径追赶外力矩。

这可用右手定则判定。即伸直右手,大拇指与食指垂直,手指顺着自转轴的方向,手掌朝外力矩的正方向,然后手掌与4指弯曲握拳,则大拇指的方向就是进动角速度的方向。
进动的角速度大小与外加的力矩成正比,与陀螺仪本身的角速度(或者说陀螺仪的旋转速度)成反比。即进动的角速度 = 施加的力矩 / 陀螺仪的角速度。
进动角速度的大小取决于转子动量矩H的大小和外力矩M的大小,其计算式为进动角速度ω=M/H。
进动性的大小也有三个影响的因素:
- 外界作用力愈大,其进动角速度也愈大;
- 转子的转动惯量愈大,进动角速度愈小;
- 转子的角速度愈大,进动角速度愈小。
你可以想象一个正在旋转的陀螺,如果你轻轻地推它,你可能会预期它会向你施加的力的方向倾倒。然而真正发生的情况是,陀螺并不会立即倾倒,而是它的顶部会开始向侧面移动。这个现象就是我们称之为"陀螺进动"的物理行为。
这种现象的原因是受力后,陀螺试图改变其旋转轴的方向,但由于角动量守恒的原则,它不能立即这么做。取而代之的是,它的旋转轴朝着原力方向的垂直方向移动。这就像你打旋的篮球,在被你手指顶住后,篮球并不会向你的手指方向倾倒,而会围绕手指转起来。
简单的说,对陀螺施加的力引起的是陀螺自身旋转轴的移动,而不是陀螺向力的方向移动,这就是陀螺的进动性。
5、陀螺仪的应用
- 陀螺仪自被发明开始,就用于导航,先是德国人将其应用在V1、V2火箭上,因此,如果配合GPS,手机的导航能力将达到前所未有的水准。实际上,很多专业手持式GPS上也装了陀螺仪,如果手机上安装了相应的软件,导航能力绝不亚于很多船舶、飞机上用的导航仪。还可以实现GPS的惯性导航:当汽车行驶到隧道或城市高大建筑物附近,没有GPS讯号时,可以通过陀螺仪来测量汽车的偏航或直线运动位移,从而继续导航。
- 可以和手机上的摄像头配合使用,比如防抖,在拍照时的维持图像的稳定,防止由于手的抖动对拍照质量的影响。在按下快门时,记录手的抖动动作,将手的抖动反馈给图像处理器,可以让手机捕捉到更清晰稳定的画面。
- 各类游戏的传感器,比如飞行游戏,体育类游戏,甚至包括一些第一视角类射击游戏,陀螺仪完整监测游戏者手的位移,从而实现各种游戏操作效果。有关这点,想必用过任天堂WII的网友会有很深的感受。
- 可以用作输入设备,陀螺仪相当于一个立体的鼠标,这个功能和第三大用途中的游戏传感器很类似,甚至可以认为是一种类型。通过小幅度的倾斜,偏转手机,实现菜单,目录的选择和操作的执行。(比如前后倾斜手机,实现通讯录条目的上下滚动;左右倾斜手机,实现浏览页面的左右移动或者页面的放大或缩小。)
- 也是未来最有前景和应用范围的用途。那就是可以帮助手机实现很多增强现实的功能。增强现实是才冒出的概念,和虚拟现实一样,是计算机的一种应用。大意是可以通过手机或者电脑的处理能力,让人们对现实中的一些物体有更深入的了解。如果大家不理解,举个例子,前面有一个大楼,用手机摄像头对准它,马上就可以在屏幕上得到这座大楼的相关参数,比如楼的高度,宽度,海拔,如果连接到数据库,甚至可以得到这座大厦的物主、建设时间、现在的用途、可容纳的人数等等。