数据结构学习笔记三:算符优先算法
给出一个表达式 2*(3-1),迅雷不及掩耳,立马知道答案为4,但是计算机可没有这样的能耐,它只知道直接计算,却不知道优先级。如此,我们需要自己用代码来告诉它算符的优先级
- 从左至右
- 先乘除后加减
- 先括号内后括号外
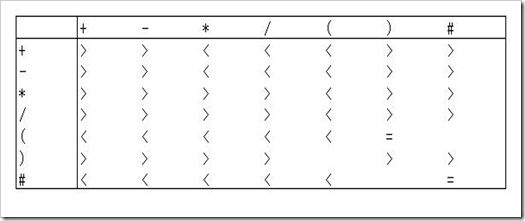
先来研究简单的算术表达式,只有+-*/()运算符
算符优先表如上图,其中#为结束标识符。
现在来纠结具体的实现。
/// <summary> /// 返回两运算符的优先级 /// </summary> /// <param name="first"></param> /// <param name="last"></param> /// <returns>">, < , ="</returns> private char Precede(char first, char last) { string operate = "+-*/()#"; char[,] level = new char[7, 7]{ {'>','>','<','<','<','>','>'}, {'>','>','<','<','<','>','>'}, {'>','>','>','>','<','>','>'}, {'>','>','<','<','<','>','>'}, {'<','<','<','<','<','=',' '}, {'>','>','>','>',' ','>','='}, {'<','<','<','<','<',' ','='} }; int rows = operate.IndexOf(first); int cols = operate.IndexOf(last); return level[rows, cols]; }
主要是来展示表中的内容,返回>,<,=.
算术表达式的计算算法,参数假设为标准的中缀表达式,否则会出现异常
/// <summary> /// 算符优先算法 /// </summary> /// <param name="infixExpression">中缀表达式</param> /// <returns></returns> public int ComputeExpression(string infixExpression) { Stack<int> stackOperand = new Stack<int>(); //操作数栈 Stack<char> stackOperator = new Stack<char>(); //操作符栈 stackOperator.Push('#'); //作为栈空的结束符 infixExpression = infixExpression + "#"; //中缀表达式的结束符 int temp = 0; int result = 0; int count = 0; char cur = infixExpression[count]; while (cur != '#' || stackOperator.Peek() != '#') //扫描完算术表达式,并且操作符栈为空 { if (cur == ' ') continue; if (IsOperand(cur)) //操作数直接入栈 { stackOperand.Push(Int32.Parse(cur.ToString())); cur = infixExpression[++count]; //扫描算术表达式下一位 } else { switch (Precede(stackOperator.Peek(), cur)) //比较操作符栈顶元素和扫描的当前算符的优先级 { //当前运算符优先级较大,则直接入栈,置于栈顶(优先级高需先计算) case '<': stackOperator.Push(cur); cur = infixExpression[++count]; break; //等于则表示栈顶元素为左括号,当前字符为右括号 case '=': stackOperator.Pop();//弹出左括号 cur = infixExpression[++count]; break; //当前运算符优先级小,则弹出栈顶运算符并从操作数栈弹出两个操作数 case '>': temp = stackOperand.Pop(); result = stackOperand.Pop(); //注意计算的顺序,计算结果入操作数栈,并且继续比较新的栈顶操作符和当前操作符的优先级 stackOperand.Push(Operate(result, temp, stackOperator.Pop())); break; } } } return stackOperand.Peek(); }
以上方法是直接接受中缀表达式来计算结果,在应用方面有
计算器(更多的操作符,而且不一定都是二目运算符),相信也不难扩展
过滤方法(一般论坛的过滤算法都是framework中的contains方法),contains方法只能为(s1and s2 and s3…),算符优先算法则可以 ( s1and s2) or (s3) ) and s4等一系列的负责表达式
算符优先算法还有一种是 先将标准的中缀表达式转换为后缀表达式(逆波兰式),然后用一个用来存储计算结果的栈来实现逆波兰式计算。
不详讲
public string InfixToPostfix(string infixExpression) { Stack<char> stackOperand = new Stack<char>(); //操作数 Stack<char> stackOperator = new Stack<char>(); //运算符 for (int i = 0; i < infixExpression.Length; i++) { if (infixExpression[i] == ' ') continue; char oper = infixExpression[i]; switch (oper) { case '+': case '-': while (stackOperator.Count > 0) { char ch = stackOperator.Peek(); if (GetOperatorPriority('-') <= GetOperatorPriority(ch)) { stackOperator.Pop(); stackOperand.Push(ch); } else { break; } } stackOperator.Push(oper); break; case '*': case '/': while (stackOperator.Count > 0) { char ch = stackOperator.Peek(); if (GetOperatorPriority('*') <= GetOperatorPriority(ch)) { stackOperator.Pop(); stackOperand.Push(ch); } else { break; } } stackOperator.Push(oper); break; case '(': stackOperator.Push(oper); break; case ')': while (stackOperator.Count > 0 && stackOperator.Peek() != '(') { char ch = stackOperator.Pop(); stackOperand.Push(ch); } stackOperator.Pop(); break; default: stackOperand.Push(oper); break; } } while (stackOperator.Count > 0) { stackOperand.Push(stackOperator.Pop()); } StringBuilder sb = new StringBuilder(); for (int i = stackOperand.Count; i > 0; i--) { sb.Insert(0, stackOperand.Pop()); } return sb.ToString(); }
public int ComputeArithmeticExpression(string postfixExpression) { Stack<int> stackResult = new Stack<int>(); int result = 0; int temp = 0; // for (int i = 0; i < postfixExpression.Length; i++) { char expr = postfixExpression[i]; switch (expr) { case '+': result = stackResult.Pop() + stackResult.Pop(); stackResult.Push(result); break; case '-': temp = stackResult.Pop(); result = stackResult.Pop() - temp; stackResult.Push(result); break; case '*': result = stackResult.Pop() * stackResult.Pop(); stackResult.Push(result); break; case '/': temp = stackResult.Pop(); result = stackResult.Pop() / temp; break; default: stackResult.Push(Int32.Parse(expr.ToString())); break; } } result = stackResult.Pop(); return result; }