在透视投影中物体z分量大小的变化
概念:
透视投影是用中心投影法将形体投射到投影面上,从而获得的一种较为接近视觉效果的单面投影图。它具有消失感、距离感、相同大小的形体呈现出有规律的变化等一系列的透视特性,能逼真地反映形体的空间形象。
透视投影符合人们心理习惯,即离视点近的物体大,离视点远的物体小,远到极点即为消失,成为灭点。它的视景体类似于一个顶部和底部都被切除掉的棱椎,也就是棱台。这个投影通常用于动画、视觉仿真以及其它许多具有真实性反映的方面。
投影变换
透视投影的过程,如图,通过将左图变换为右图,再通过正交投影投射到摄像机上去。
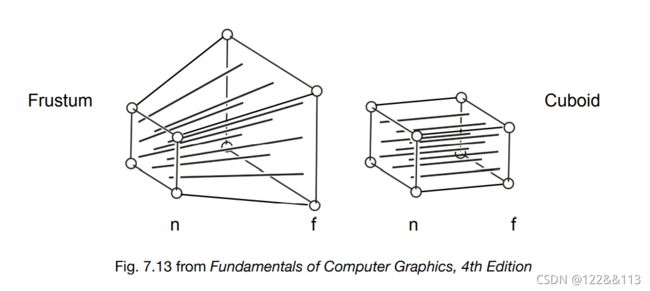
问题?
已知条件:
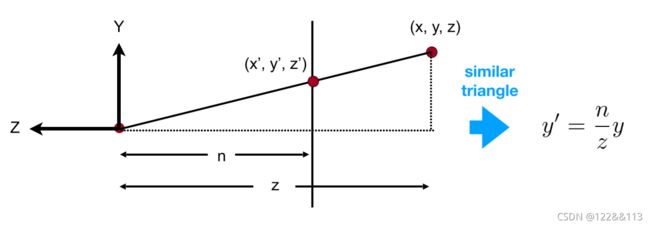
n n n 表示距离摄像机最近的一个平面的距离
f f f 表示距离摄像机最远的一个平面的距离
摄像机的位置在原点,且朝向为 − z -z −z 方向,因此该物体中 z z z 轴上的定义域为 [ f , n ] [f, n] [f,n]
该物体中某个点的位置,用齐次坐标表示为:
( x y z 1 ) \begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} ⎝ ⎛xyz1⎠ ⎞
由上图可得:
y ′ = n z y , x ′ = n z x y' = \frac{n}{z}y, x' = \frac{n}{z}x y′=zny,x′=znx
这里 z z z 轴上的点还无法确定,只是知道在近平面上的点都不会发生变换,远平面上的点 z z z 轴不变
因此可以先提取一部分变换矩阵:
( n 0 0 0 0 n 0 0 0 0 ? ? 0 0 1 0 ) ( x y z 1 ) = ( x ′ y ′ ? 1 ) = ( n x n y ? z ) ⇒ ( n x z n y z ? 1 ) \begin{pmatrix} n & 0 & 0 &0 \\ 0 & n & 0 &0 \\ 0 & 0 & ? & ? \\ 0 & 0 & 1 &0 \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}= \begin{pmatrix} x'\\ y'\\ ?\\ 1 \end{pmatrix}= \begin{pmatrix} nx\\ ny\\ ?\\ z \end{pmatrix}\Rightarrow \begin{pmatrix} \frac{nx}{z}\\ \frac{ny}{z}\\ ?\\ 1 \end{pmatrix} ⎝ ⎛n0000n0000?100?0⎠ ⎞⎝ ⎛xyz1⎠ ⎞=⎝ ⎛x′y′?1⎠ ⎞=⎝ ⎛nxny?z⎠ ⎞⇒⎝ ⎛znxzny?1⎠ ⎞
现在根据特殊值来解这个矩阵,根据在近平面和远平面的条件我们可以得到关于 ? ? ? 那一行的方程组:
s e t : ( n 0 0 0 0 n 0 0 0 0 A B 0 0 1 0 ) set: \begin{pmatrix} n & 0 & 0 &0 \\ 0 & n & 0 &0 \\ 0 & 0 & A &B \\ 0 & 0 & 1 &0 \end{pmatrix} set:⎝ ⎛n0000n0000A100B0⎠ ⎞
近平面: z = n z=n z=n
( n 0 0 0 0 n 0 0 0 0 A B 0 0 1 0 ) ( x y n 1 ) = ( n x n y ? = n 2 n ) ⇒ ( n x n = x n y n = y n 2 n = n n n = 1 ) \begin{pmatrix} n & 0 & 0 &0 \\ 0 & n & 0 &0 \\ 0 & 0 & A & B \\ 0 & 0 & 1 &0 \end{pmatrix} \begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix}= \begin{pmatrix} nx\\ ny\\ ?=n^2\\ n \end{pmatrix}\Rightarrow \begin{pmatrix} \frac{nx}{n} = x\\ \frac{ny}{n} = y\\ \frac{n^2}{n} = n\\ \frac{n}{n} = 1 \end{pmatrix} ⎝ ⎛n0000n0000A100B0⎠ ⎞⎝ ⎛xyn1⎠ ⎞=⎝ ⎛nxny?=n2n⎠ ⎞⇒⎝ ⎛nnx=xnny=ynn2=nnn=1⎠ ⎞
A n + B = n 2 An+B=n^2 An+B=n2
远平面: z = f z=f z=f
( n 0 0 0 0 n 0 0 0 0 A B 0 0 1 0 ) ( x y f 1 ) = ( f x f y ? = f 2 f ) ⇒ ( f x f = x f y f = y f 2 f = n f f = 1 ) \begin{pmatrix} n & 0 & 0 &0 \\ 0 & n & 0 &0 \\ 0 & 0 & A & B \\ 0 & 0 & 1 &0 \end{pmatrix} \begin{pmatrix} x\\ y\\ f\\ 1 \end{pmatrix}= \begin{pmatrix} fx\\ fy\\ ?=f^2\\ f \end{pmatrix}\Rightarrow \begin{pmatrix} \frac{fx}{f} = x\\ \frac{fy}{f} = y\\ \frac{f^2}{f} = n\\ \frac{f}{f} = 1 \end{pmatrix} ⎝ ⎛n0000n0000A100B0⎠ ⎞⎝ ⎛xyf1⎠ ⎞=⎝ ⎛fxfy?=f2f⎠ ⎞⇒⎝ ⎛ffx=xffy=yff2=nff=1⎠ ⎞
A f + B = f 2 Af+B=f^2 Af+B=f2
方程组:
{ A n + B = n 2 A f + B = f 2 \begin{cases} An+B =n^2 \\ Af+B =f^2 \end{cases} {An+B=n2Af+B=f2
解得:
{ A = n + f B = − n f \begin{cases} A =n+f \\ B =-nf \end{cases} {A=n+fB=−nf
故现在可得变换矩阵为:
( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) \begin{pmatrix} n & 0 & 0 &0 \\ 0 & n & 0 &0 \\ 0 & 0 & n+f &-nf \\ 0 & 0 & 1 &0 \end{pmatrix} ⎝ ⎛n0000n0000n+f100−nf0⎠ ⎞
z 分量会在这个变换过程中有什么变化?
那么根据games101-闫令琪老师提出的一个思考问题,物体坐标中的 z z z 分量会在这个变换过程中有什么变化?
前面的都是铺垫,后面才是解决这个问题的正文。
首先可以设一个坐标点:
( x y z 1 ) \begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} ⎝ ⎛xyz1⎠ ⎞
将变换矩阵与其相乘得到变换后的坐标:
( n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ) ( x y z 1 ) = ( n x z = x ′ n y z = y ′ ( n + f ) z − n f z = z ′ z z = 1 ) \begin{pmatrix} n & 0 & 0 &0 \\ 0 & n & 0 &0 \\ 0 & 0 & n+f &-nf \\ 0 & 0 & 1 &0 \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}= \begin{pmatrix} \frac{nx}{z} = x'\\ \frac{ny}{z} = y'\\ \frac{(n+f)z-nf}{z} = z'\\ \frac{z}{z} = 1 \end{pmatrix} ⎝ ⎛n0000n0000n+f100−nf0⎠ ⎞⎝ ⎛xyz1⎠ ⎞=⎝ ⎛znx=x′zny=y′z(n+f)z−nf=z′zz=1⎠ ⎞
此时可以设方程:
f ( z ) = z ′ − z = ( n + f ) − n f z − z , z ∈ [ f , n ] f(z) = z'-z=(n+f)-\frac{nf}{z}-z, z\in[f,n] f(z)=z′−z=(n+f)−znf−z,z∈[f,n]
对其求导:
f ′ ( z ) = n f z 2 − 1 , z ∈ [ f , n ] f'(z) = \frac{nf}{z^2}-1, z\in[f,n] f′(z)=z2nf−1,z∈[f,n]
输入: z = n , z = f z=n ,z=f z=n,z=f
注意,这里需要明确 n < 0 , f < 0 n < 0,f < 0 n<0,f<0,之前确实忽略了这一点,由评论中 little little bin
指出
{ f ′ ( n ) = f n − 1 > 0 f ′ ( f ) = n f − 1 < 0 \begin{cases} f'(n) =\frac{f}{n}-1 > 0 \\ f'(f) =\frac{n}{f}-1 < 0 \end{cases} {f′(n)=nf−1>0f′(f)=fn−1<0
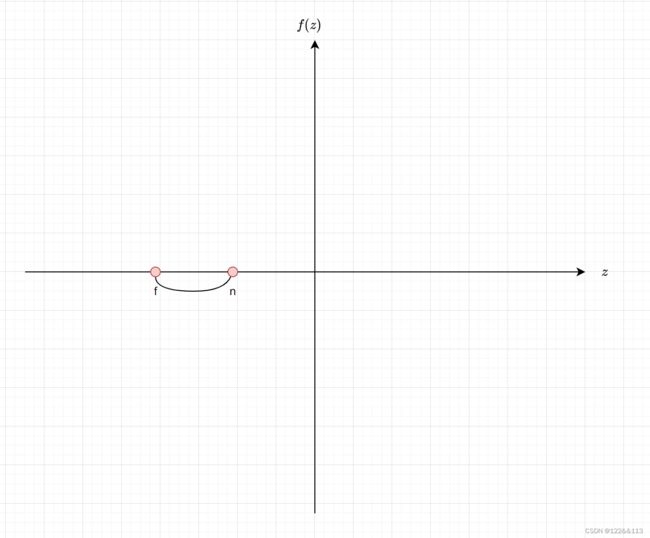
那么可以在坐标轴上表示其关系:
结论
由图可知,在 [ f , n ] [f,n] [f,n]上都有
f ( z ) = z ′ − z < 0 f(z)=z'-z<0 f(z)=z′−z<0
因此物体中的某个位置在变换过程中 z z z 分量会变小,但是从绝对值来说是增大。