【图像误差测量】测量 2 张图像之间的差异，并测量图像质量（Matlab代码实现）

 欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

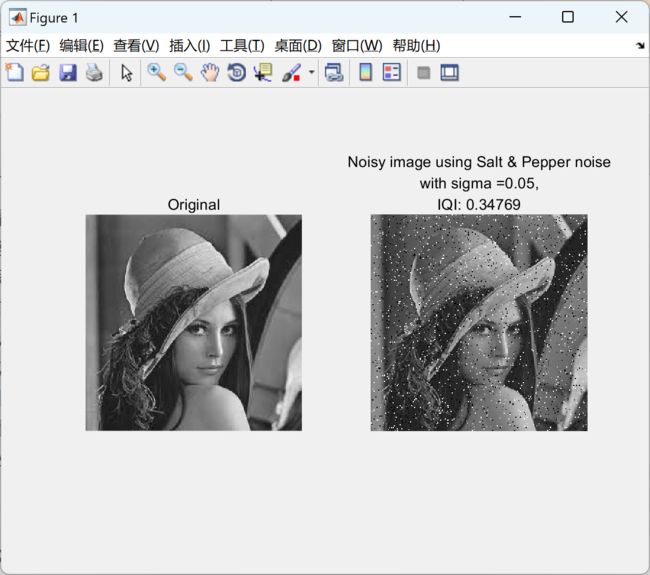
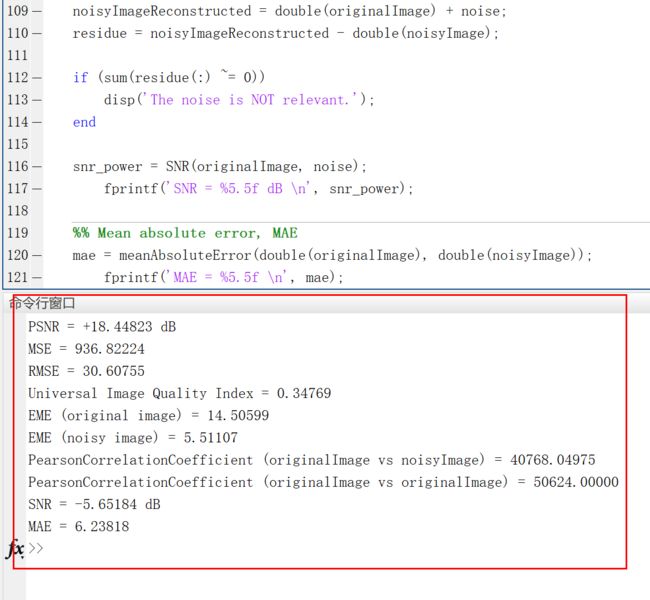
2 运行结果

3 参考文献

4 Matlab代码实现

---

1 概述

【图像误差测量】测量 2 张图像之间的差异，并测量图像质量

图像误差测量是一项重要的研究领域，旨在开发有效的方法来量化和评估图像之间的差异。这些差异可以来自于图像处理、压缩、传输或其他图像处理过程中的各种因素。

在图像处理领域，准确地测量图像之间的误差是评估算法效果和优化算法的关键。通过比较原始图像和经过处理后的图像，可以确定图像处理算法对图像所做的修改，并评估其对图像质量的影响。

常用的图像误差测量方法包括：

- 均方误差 (MSE)：计算两幅图像的像素之间差值的平方的平均值。较大的MSE值表示较大的差异。

- 峰值信噪比 (PSNR)：通过比较两幅图像的动态范围和均方误差来评估图像质量。PSNR值越高，表示图像质量越好。

- 结构相似性指数 (SSIM)：通过比较图像的亮度、对比度和结构信息等方面的相似性来评估图像的质量。较高的SSIM值表示较高的相似性。

- 互信息 (MI)：衡量两幅图像之间的信息重叠程度。较高的互信息值表示较高的相似性。

- 泊松噪声比 (PNR)：通过估计图像中的噪声和估计信号之间的比值来评估图像质量。较高的PNR值表示较好的图像质量。

另外，随着深度学习和人工智能的发展，还涌现出一些基于神经网络的图像误差测量方法，如基于卷积神经网络 (CNN) 的结构相似度指数 (CNN-SSIM) 和感知损失 (Perceptual Loss) 等。

图像误差测量的研究旨在改进现有的方法，并开发新的有效算法来更准确地评估图像之间的差异。这些研究对于图像处理任务如图像复原、超分辨率、图像压缩和图像质量评估等具有重要的实际应用价值。通过深入研究图像误差测量，我们可以更好地理解图像的特性，并为相关领域的进一步发展提供指导和支持。

本文旨在测量两张图像之间的差异并评估图像质量。以下是常用的几种图像误差测量方法：

1. 均方误差 (MSE)：计算两张图像像素之间差值的平方的平均值。这个指标越小，表示两张图像越相似。

2. 均方根误差 (RMSE)：将均方误差的结果开方，以得到具有与原始像素单位一致的测量值。

3. 峰值信噪比 (PSNR)：通过比较两张图像的动态范围和均方误差来衡量图像质量。这个指标的值越高，表示两张图像之间的差异越小，图像质量越高。

4. 平均绝对误差 (MAE)：计算两张图像像素之间差值的绝对值的平均值。与均方误差不同，MAE更加关注图像中的小差异。

5. 信噪比 (SNR)：通过比较图像中有用信号的强度与噪声的强度来评估图像的质量。一个较高的信噪比表示图像中有较少的噪声干扰。

6. 通用图像质量指数 (IQI)：综合考虑了图像的亮度、对比度、锐度和颜色等方面的信息，以评估图像的整体质量。

7. 增强测量误差 (EME)：通过将图像的增强后版本与原始版本进行比较，来衡量图像的质量提升程度。

8. 皮尔逊相关系数：衡量两张图像之间的线性相关性。当相关系数接近于1时，表示两张图像高度相关；当接近于0时，表示两张图像不相关。

通过使用这些图像误差测量方法，我们可以客观地评估图像之间的差异并量化图像质量。这些指标对于图像处理和图像质量控制非常重要，可以帮助我们优化和改进图像处理算法，并提供更好的视觉体验。

2 运行结果

部分代码：

noiseTypeModes = {
    'gaussian',         % [1]
    'salt & pepper',    % [2]    
    'localvar',         % [3]
    'speckle',          % [4] (multiplicative noise)
    'poisson',          % [5]
    'motion blur',      % [6]
    'erosion',          % [7]
    'dilation',         % [8]
    % 'jpg compression blocking effect'   % [9]
    % [10] Interpolation/ resizing noise 
    };

noiseChosen = 2;
noiseTypeChosen = char(noiseTypeModes(noiseChosen));

originalImage = uint8(IMG);

%% plot original
titleStr = 'Original';

imagePlot( originalImage, plotRowSize, plotColSize, ...
                    plotIndex, titleStr );
plotIndex = plotIndex + 1;

%%
for i = 1:(plotRowSize*plotColSize)-1

IMG_aforeUpdated = double(IMG);    % backup the previous state just in case it gets updated.

% returns the noise param updates for further corruption    
% IMG may be updated as the noisy image for the next round
[IMG, noisyImage, titleStr, sigma, dilationFilterSize, erosionFilterSize] = ...
    noisyImageGeneration(IMG, mean, sigma, offset, dilationFilterSize, erosionFilterSize, noiseTypeChosen);

imageQualityIndex_Value = imageQualityIndex(double(originalImage), double(noisyImage));

titleStr = [titleStr ',' newline 'IQI: ' num2str(imageQualityIndex_Value)];

imagePlot( noisyImage, plotRowSize, plotColSize, ...
                    plotIndex, titleStr );
plotIndex = plotIndex + 1;

end

if (~strcmp(char(class(noisyImage)), 'uint8'))
    disp('noisyImage is NOT type: uint8');
end

%% PSNR
psnr_Value = PSNR(originalImage, noisyImage);
    fprintf('PSNR = +%5.5f dB \n', psnr_Value);
%% RMSE
[mse, rmse] = RMSE2(double(originalImage), double(noisyImage));
    fprintf('MSE = %5.5f \n', mse);
    fprintf('RMSE = %5.5f \n', rmse);
%% Universal Quality Index
imageQualityIndex_Value = imageQualityIndex(double(originalImage), double(noisyImage));
    fprintf('Universal Image Quality Index = %5.5f \n', imageQualityIndex_Value);
%% Enhancement : measure of enhance- ment, or measure of improvement
[M M] = size(originalImage);
L = 8;
EME_original = eme(double(originalImage),M,L);
EME_noisyImage = eme(double(noisyImage),M,L);
    fprintf('EME (original image) = %5.5f \n', EME_original);
    fprintf('EME (noisy image) = %5.5f \n', EME_noisyImage);
%% PearsonCorrelationCoefficient
pcc = compute_PearsonCorrelationCoefficient (double(originalImage), double(noisyImage));
    fprintf('PearsonCorrelationCoefficient (originalImage vs noisyImage) = %5.5f \n', pcc);
pcc = compute_PearsonCorrelationCoefficient (double(originalImage), double(originalImage));
    fprintf('PearsonCorrelationCoefficient (originalImage vs originalImage) = %5.5f \n', pcc);

%% Signal to signal noise ratio, SNR
noise = double(noisyImage) - double(originalImage); % assume additive noise

% check noise
noisyImageReconstructed = double(originalImage) + noise;
residue = noisyImageReconstructed - double(noisyImage);

if (sum(residue(:) ~= 0))
    disp('The noise is NOT relevant.');
end

snr_power = SNR(originalImage, noise);
    fprintf('SNR = %5.5f dB \n', snr_power);
    
%% Mean absolute error, MAE
mae = meanAbsoluteError(double(originalImage), double(noisyImage));
    fprintf('MAE = %5.5f \n', mae);

noiseTypeModes = {
    'gaussian',         % [1]
    'salt & pepper',    % [2]    
    'localvar',         % [3]
    'speckle',          % [4] (multiplicative noise)
    'poisson',          % [5]
    'motion blur',      % [6]
    'erosion',          % [7]
    'dilation',         % [8]
    % 'jpg compression blocking effect'   % [9]
    % [10] Interpolation/ resizing noise
    };

noiseChosen = 2;
noiseTypeChosen = char(noiseTypeModes(noiseChosen));

originalImage = uint8(IMG);

%% plot original
titleStr = 'Original';

imagePlot( originalImage, plotRowSize, plotColSize, ...
                    plotIndex, titleStr );
plotIndex = plotIndex + 1;

%%
for i = 1:(plotRowSize*plotColSize)-1

IMG_aforeUpdated = double(IMG);    % backup the previous state just in case it gets updated.

% returns the noise param updates for further corruption    
% IMG may be updated as the noisy image for the next round
[IMG, noisyImage, titleStr, sigma, dilationFilterSize, erosionFilterSize] = ...
    noisyImageGeneration(IMG, mean, sigma, offset, dilationFilterSize, erosionFilterSize, noiseTypeChosen);

imageQualityIndex_Value = imageQualityIndex(double(originalImage), double(noisyImage));

titleStr = [titleStr ',' newline 'IQI: ' num2str(imageQualityIndex_Value)];

imagePlot( noisyImage, plotRowSize, plotColSize, ...
                    plotIndex, titleStr );
plotIndex = plotIndex + 1;

end

if (~strcmp(char(class(noisyImage)), 'uint8'))
    disp('noisyImage is NOT type: uint8');
end

%% PSNR
psnr_Value = PSNR(originalImage, noisyImage);
    fprintf('PSNR = +%5.5f dB \n', psnr_Value);
%% RMSE
[mse, rmse] = RMSE2(double(originalImage), double(noisyImage));
    fprintf('MSE = %5.5f \n', mse);
    fprintf('RMSE = %5.5f \n', rmse);
%% Universal Quality Index
imageQualityIndex_Value = imageQualityIndex(double(originalImage), double(noisyImage));
    fprintf('Universal Image Quality Index = %5.5f \n', imageQualityIndex_Value);
%% Enhancement : measure of enhance- ment, or measure of improvement
[M M] = size(originalImage);
L = 8;
EME_original = eme(double(originalImage),M,L);
EME_noisyImage = eme(double(noisyImage),M,L);
    fprintf('EME (original image) = %5.5f \n', EME_original);
    fprintf('EME (noisy image) = %5.5f \n', EME_noisyImage);
%% PearsonCorrelationCoefficient
pcc = compute_PearsonCorrelationCoefficient (double(originalImage), double(noisyImage));
    fprintf('PearsonCorrelationCoefficient (originalImage vs noisyImage) = %5.5f \n', pcc);
pcc = compute_PearsonCorrelationCoefficient (double(originalImage), double(originalImage));
    fprintf('PearsonCorrelationCoefficient (originalImage vs originalImage) = %5.5f \n', pcc);

%% Signal to signal noise ratio, SNR
noise = double(noisyImage) - double(originalImage); % assume additive noise

% check noise
noisyImageReconstructed = double(originalImage) + noise;
residue = noisyImageReconstructed - double(noisyImage);

if (sum(residue(:) ~= 0))
    disp('The noise is NOT relevant.');
end

snr_power = SNR(originalImage, noise);
    fprintf('SNR = %5.5f dB \n', snr_power);
    
%% Mean absolute error, MAE
mae = meanAbsoluteError(double(originalImage), double(noisyImage));
    fprintf('MAE = %5.5f \n', mae);

3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]路慧娟.影像测量误差实验估计[D].西安体育学院[2023-09-21].DOI:10.7666/d.d142172.

[2]康立丽,林意群,林木炎.MR信噪比一幅图像测量方法与两幅图像测量方法对照研究[J].北京生物医学工程, 2004, 23(1):4.DOI:10.3969/j.issn.1002-3208.2004.01.002.

[3]吴晓波,安文斗.图像测量系统中的误差分析及提高测量精度的途径[J].光学精密工程, 1997, 5(1):12.DOI:CNKI:SUN:GXJM.0.1997-01-022.

[4]廖强华,钟江生.基于图像处理的光纤阵列误差测量[J].计算机工程, 2006, 32(10):3.DOI:10.3969/j.issn.1000-3428.2006.10.097.

4 Matlab代码实现