石器时代 —— Leetcode刷题日记 (二 数据结构)
算法是寻找思维定式的思维
后篇 - 算法思维
文章目录
- 1 `数据结构相关`
- 简单系统设计 - Twitter
- 简单系统设计 - 计算器
-
- L772 基本计算器III
- 结构实现
-
- 队列/栈 互相实现
-
- L232 用栈实现队列
- L225 用队列实现栈
- 最大/最小堆 Heap
-
- L703. 数据流中的第K大元素
-
- W1 小顶堆实现 - Priority_queue
- W2 二叉搜索数实现 - 红黑树 - Multiset
- 数据缓存机制
-
- LRU缓存
- LFU缓存
- 单调栈&单调队列
-
- 单调栈 Monotonic Stack
-
- L739 每日温度
- 496 下一个更大的数
- 503 下一个更大的数 (循环)
- 556 下一个更大数(单个数)
- 402 移掉k位数字
- 316 去除重复字母
- 321 拼接最大数
- 单调队列
-
- L239 滑动窗口最大值
- 有序表 Ordered map
-
- 855. 考场就座
-
- 849 到最近人的最大距离
- 拓展:855 考生就坐
-
- `W1 一维数组类型`
- `W2 有序set类型`
- 栈
-
- 括号合法性
-
- 单种括号的情况
- 多括号 - 栈方法
- 队列
- 链表
-
- 回文链表
-
- 链表的后序遍历 O(n)空间复杂
- 快慢指针+反转
- 206 反转列表
-
- `W1 双指针法`
- `W2 递归法`
- 92 反转m~n间的链表
-
- `W1 递归`
- `W2 迭代`
- 25 K个一组反转链表
- 143 重排链表
- `树`
-
- 二叉树遍历
-
- 前序遍历(迭代)
- 中序遍历(迭代)
- 后序遍历(迭代)
- 二叉树前序+中序遍历 > 后序
- 完全二叉树
-
- L222 求完全二叉树的节点数
- 二叉搜索树
-
- 判断
-
- `W1 递归法`
- `W2 中序遍历法`
- 查询
- 插入
- 删除
- 99 二叉搜索树恢复
-
- `W1 DFS`
- `W2 Stack`
- `W3 Morris遍历 方法 O(1)空间复杂度`
- 255 判断数组是不是二叉搜索树的前序遍历
- 最优二叉搜索树
- 124 计算二叉树的最大路径和
- 105&106 二叉树还原
-
-
- `W1 105 先序+中序`
- `W2 106 中序+后序`
- W3 889 前序+后序,返回其中一个可能的树序列
-
- 红黑树 / RBT
-
- 旋转
- 增加
- 删除
- 数组中树的思想
-
- 最大/最小堆
- 二叉索引树/ 树状数组 Binary Indexed Tree
- 线段树 Segment Tree
- 离散化
- 字符串操作中树的思想
- 字符编码中树的思想
- 图
-
- 图的表示
- 图的连通性
-
- Kosaraju算法
- 二分图
- 最短路径
-
- Dijkstra算法 不能处理负权
-
- 朴素版dijkstra适合稠密图
- 堆优化版dijkstra适合稀疏图
- 最小生成树
- 并查集算法 Union-find
-
- 原理
-
- 树的平衡性优化 / 启发式(按秩)合并
- 路径压缩
- 回滚并查集 / 带撤销并查集
- 可持久化并查集 TODO
- 应用
-
- 130. 被围绕的区域
-
-
- W1 DFS
- W2 BFS
- W3 Union-find
-
- 990. 等式方程的可满足性
- 拓扑排序
1 数据结构相关
简单系统设计 - Twitter
1 postTweet(userId, tweetId): 创建一条新的推文
2 getNewsFeed(userId): 检索最近的十条推文。每个推文都必须是由此用户关注的人或者是用户自己发出的。推文必须按照时间顺序由最近的开始排序。
3 follow(followerId, followeeId): 关注一个用户
4 unfollow(followerId, followeeId): 取消关注一个用户
主要是第三个函数的推文排序问题! 利用STL的话,可以用两种方法,一是map的红黑树键值自动排序;二是priority_queue的二叉堆排序:priority_queue
代码如下:
class Twitter {
private:
int time;
unordered_map<int, unordered_set<int>> friends;
unordered_map<int, map<int,int,greater<int>>> tweets; // 利用了map中红黑树自动排序
public:
/** Initialize your data structure here. */
Twitter() {
time++;
}
/** Compose a new tweet. */
void postTweet(int userId, int tweetId) {
follow(userId, userId);
tweets[userId].emplace(time++,tweetId);
}
/** Retrieve the 10 most recent tweet ids in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user herself. Tweets must be ordered from most recent to least recent. */
vector<int> getNewsFeed(int userId) {
vector<int> res;
map<int,int,greater<int>> top10;
for (auto& p : friends[userId]) {
for (auto& t : tweets[p]) {
top10.emplace(t.first, t.second);
if (top10.size() > 10) top10.erase(--top10.end());
}
}
for (auto& tt : top10) res.push_back(tt.second);
return res;
}
/** Follower follows a followee. If the operation is invalid, it should be a no-op. */
void follow(int followerId, int followeeId) {
friends[followerId].emplace(followeeId);
}
/** Follower unfollows a followee. If the operation is invalid, it should be a no-op. */
void unfollow(int followerId, int followeeId) {
if (followeeId != followerId)
friends[followerId].erase(followeeId);
}
};
简单系统设计 - 计算器
L772 基本计算器III
包括数字/括号/加减乘除,认为算式是合法的!
- 将数字正负替换加减概览,保存在栈中;
- 乘除法优先于加减法体现在,乘除法可以和栈顶的数结合,而加减法只能把自己放入栈;
- 空格跳过就行;
- 括号具有递归性质,遇到(开始递归,遇到)结束递归,括号包含的算式,我们直接视为一个数字!
class Solution {
private:
bool isDigital(char c) {
return c >= '0' && c <= '9';
}
public:
int calculate(string& s) {
stack<int> st;
int num = 0;
char sgn = '+';
while (s.size()) {
char c = s[0]; s.erase(s.begin());
if (isDigital(c)) num = 10*num+(c-'0');
if (c == '(') num = calculate(s);
if ((!isDigital(c) && c!=' ') || s.size() == 0) {
switch (sgn) { // 算子
case '+': st.push(num); break;
case '-': st.push(-num); break;
case '*': st.top()*=num; break;
case '/': st.top()/=num; break;
}
sgn = c;
num = 0;
}
if (c == ')') break;
}
int res = 0;
while (!st.empty()) {
res += st.top(); st.pop();
}
return res;
}
};
上面代码超时!
下面直接迭代求解:
class Solution {
public:
int calculate(string s) {
int n = s.size(), num = 0, curRes = 0, res = 0;
char op = '+';
for (int i = 0; i < n; ++i) {
char c = s[i];
if (c >= '0' && c <= '9') {
num = num * 10 + (c - '0');
} else if (c == '(') {
int j = i, cnt = 0;
for (; i < n; ++i) {
if (s[i] == '(') ++cnt;
if (s[i] == ')') --cnt;
if (cnt == 0) break;
}
num = calculate(s.substr(j + 1, i - j - 1));
}
if (c == '+' || c == '-' || c == '*' || c == '/' || i == n - 1) {
switch (op) {
case '+': curRes += num; break;
case '-': curRes -= num; break;
case '*': curRes *= num; break;
case '/': curRes /= num; break;
}
if (c == '+' || c == '-' || i == n - 1) {
res += curRes;
curRes = 0;
}
op = c;
num = 0;
}
}
return res;
}
};
结构实现
队列/栈 互相实现
L232 用栈实现队列
class MyQueue {
stack<int> s1, s2;
public:
/** Initialize your data structure here. */
MyQueue() {}
/** Push element x to the back of queue. */
void push(int x) {
s1.push(x);
}
/** Removes the element from in front of queue and returns that element. */
int pop() {
peek();
int res = s2.top();
s2.pop();
return res;
}
/** Get the front element. */
int peek() {
if (s2.empty()) {
while (!s1.empty()) {
s2.push(s1.top()); s1.pop();
}
}
return s2.top();
}
/** Returns whether the queue is empty. */
bool empty() {
return s1.empty() && s2.empty();
}
};
L225 用队列实现栈
class MyStack {
private:
queue<int> que;
int top_num;
public:
/** Initialize your data structure here. */
MyStack() {top_num = 0;}
/** Push element x onto stack. */
void push(int x) {
que.push(x);
top_num = x;
}
/** Removes the element on top of the stack and returns that element. */
int pop() {
int N = que.size();
while (N > 2) {
que.push(que.front());
que.pop();
N--;
}
top_num = que.front();
que.pop(); que.push(top_num);
int res = que.front();
que.pop();
return res;
}
/** Get the top element. */
int top() {
return top_num;
}
/** Returns whether the stack is empty. */
bool empty() {
return que.empty();
}
};
最大/最小堆 Heap
就是STL中priority的底层实现!
二叉堆其实就是一种特殊的二叉树(完全二叉树),只不过存储在数组里
二叉堆应用 1 优先级队列 2 堆排序
1 二叉堆的操作很简单,主要就是上浮和下沉,来维护堆的性质(堆有序),核心代码也就十行。
2 优先级队列是基于二叉堆实现的,主要操作是插入和删除。插入是先插到最后,然后上浮到正确位置;删除是调换位置后再删除,然后下沉到正确位置。核心代码也就十行。
链接
class MyHeap { // 小顶堆
public:
void push(int val) {
this->_buffer.emplace_back(val);
this->_swin(this->_buffer.size() - 1);
}
int size() {
return this->_buffer.size();
}
int top() {
return this->_buffer.front();
}
int pop() {
int r = this->_buffer.front();
this->_exch(0, this->size() - 1);
this->_buffer.pop_back();
this->_sink(0);
return r;
}
private:
vector<int> _buffer;
bool _isValid(int i) {
return i >= 0 && i < _buffer.size();
}
bool _less(int i, int j) {
return this->_buffer[i] <= this->_buffer[j];
}
void _exch(int i, int j) {
if (this->_isValid(i) && this->_isValid(j)) {
swap(this->_buffer[i], this->_buffer[j]);
}
}
int _parent(int i) {
if (!this->_isValid(i)) return -1;
return (i - 1) / 2;
}
int _left(int i) {
int r = 2 * i + 1;
if (!this->_isValid(r)) return -1;
return r;
}
int _right(int i) {
int r = 2 * i + 2;
if (!this->_isValid(r)) return -1;
return r;
}
void _swin(int k) {
while (this->_isValid(this->_parent(k))) {
if (this->_less(this->_parent(k), k)) break;
this->_exch(k, this->_parent(k));
k = this->_parent(k);
}
}
void _sink(int k) {
while (this->_isValid(this->_left(k))) {
int qin = this->_left(k);
if (this->_isValid(this->_right(k))) {
qin = this->_less(this->_right(k), qin) ? this->_right(k) : qin;
}
if (this->_less(k, qin)) break;
this->_exch(qin, k);
k = qin;
}
}
};
private void swim(int k) {
// 如果浮到堆顶,就不能再上浮了
while (k > 1 && less(parent(k), k)) {
// 如果第 k 个元素比上层大
// 将 k 换上去
exch(parent(k), k);
k = parent(k);
}
}
private void sink(int k) {
// 如果沉到堆底,就沉不下去了
while (left(k) <= N) {
// 先假设左边节点较大
int older = left(k);
// 如果右边节点存在,比一下大小
if (right(k) <= N && less(older, right(k)))
older = right(k);
// 结点 k 比俩孩子都大,就不必下沉了
if (less(older, k)) break;
// 否则,不符合最大堆的结构,下沉 k 结点
exch(k, older);
k = older;
}
}
public void insert(Key e) {
N++;
// 先把新元素加到最后
pq[N] = e;
// 然后让它上浮到正确的位置
swim(N);
}
public Key delMax() {
// 最大堆的堆顶就是最大元素
Key max = pq[1];
// 把这个最大元素换到最后,删除之
exch(1, N);
pq[N] = null;
N--;
// 让 pq[1] 下沉到正确位置
sink(1);
return max;
}
L703. 数据流中的第K大元素
W1 小顶堆实现 - Priority_queue
维护一个K容量的小顶堆,每次返回头元素就是第K大元素!
class KthLargest {
private:
// 小顶堆
priority_queue<int,vector<int>,greater<int>> que;
int cap;
public:
KthLargest(int k, vector<int>& nums) {
cap = k;
for (auto& n : nums) que.push(n);
while (que.size() > cap) que.pop();
}
int add(int val) {
que.push(val);
if (que.size() > cap) que.pop();
return que.top();
}
};
怎么实现一个堆能,并进一步实现优先级队列?
- 首先确定需要的成员函数:swim和sink(上浮和下沉)
PS: 堆不等于优先级队列,STL中priority_queue(默认使用vector类型)需要堆排序实现有序!堆排序 = 构建大(小)顶堆+交换头尾元素+头元素下沉,这样就能得到升(降)序排列的数组!堆排序代码可以参考 刷题日记(一)
void heapBuild(vector<int>& nums, int root, int end) {
// 就是小顶堆的下沉操作,将root处元素在0~end间下沉到不能下为止
int left = 2 * root + 1;
if (left >= end) return;
int right = left + 1;
// 左右子节点中的较小值序号
int minInx = ((right<end)&&(nums[right]<nums[left])) ? right : left;
if (nums[minInx] < nums[root]) {
swap(nums[minInx], nums[root]);
heapBuild(nums, minInx, end);
}
}
void heapSort(vector<int>& nums) {
// #1 初始化完全二叉树->先小顶堆方式 提取最小值到0处
for (int i = nums.size() / 2 - 1; i >= 0; --i) {
// 从倒数第二层开始开始将大值下沉,或者说小值上升
heapBuild(nums, i, nums.size());
}
// #2 交换下沉
for (int i = nums.size() - 1; i > 0; --i) {
// 交换头尾 将最小值往未排序的后面节点放
swap(nums[0], nums[i]);
heapBuild(nums, 0, i);
}
}
W2 二叉搜索数实现 - 红黑树 - Multiset
class KthLargest {
private:
// 红黑树 - BST
multiset<int, less<int>> se;
int cap;
public:
KthLargest(int k, vector<int>& nums) {
cap = k;
for (auto& n : nums) se.emplace(n);
while (se.size() > cap) se.erase(se.begin());
}
int add(int val) {
se.emplace(val);
if (se.size() > cap) se.erase(se.begin());
return *se.begin();
}
};
PS: 针对这道题的二叉搜索树BST的C++实现:
class BST {
public:
BST(int k) : k(k), root(nullptr) {}
int add(int val) {
this->root = this->_add(this->root, val);
return this->_find(this->root, this->k);
}
private:
typedef struct _Node {
_Node *left, *right;
int val, cnt;
_Node(int v): val(v), left(nullptr), right(nullptr), cnt(1) {}
} _Node;
int k;
_Node* root;
_Node* _add(_Node* root, int val) { // 建立BST过程/Greedy方法/没有红黑树优化
if (!root) return new _Node(val);
root->cnt++;
if (val <= root->val) root->left = this->_add(root->left, val);
else root->right = this->_add(root->right, val);
return root;
}
int _find(_Node* root, int k) {
if (root->cnt < k) return -1; // 找不到
int m = 1; // 当前节点和右子树的总节点数
if (root->right) m += root->right->cnt;
if (k == m) return root->val;
if (k > m) return this->_find(root->left, k - m);
return this->_find(root->right, k);
}
};
class KthLargest {
public:
KthLargest(int k, vector<int>& nums) {
this->Q = new BST(k);
for (auto& n : nums) {
this->add(n);
}
}
int add(int val) {
return this->Q->add(val);
}
private:
BST* Q;
int capacity;
};
- 上述的建立BST的过程属于贪心思路,不会考虑建立出来的BST是否合理(根节点到叶节点距离参差不齐,差距过大);可以考虑红黑树(STL的有序关联数据结构采用的红黑树)
数据缓存机制
LRU缓存
Least Recently Used,也就是说我们认为最近 使用过/访问过 的数据应该是是「有用的」,很久都没用过的数据应该是无用的,内存满了就优先删那些很久没用过的数据。(如何表示访问的优先级 >> hash表)
你是否可以在 O(1) 时间复杂度内执行两项操作?访问和插入(删除)!
哈希表方便查找,双向链表方便插入删除(因为可以访问到前后关联),所以:
class LRUCache {
public:
LRUCache(int capacity) {
this->capacity = capacity;
}
int get(int key) {
if (this->H.find(key) == this->H.end()) return -1;
this->L.splice(this->L.begin(), this->L, this->H[key]);
return this->L.front().second;
}
void put(int key, int value) {
if (this->get(key) != -1) {
this->H[key]->second = value;
return;
}
if (this->L.size() >= this->capacity) {
int key = this->L.back().first;
this->L.pop_back();
this->H.erase(key);
}
this->L.emplace_front(pair<int, int>(key, value));
this->H[key] = this->L.begin();
}
private:
list<pair<int, int> > L;
unordered_map<int, list<pair<int, int> >::iterator> H;
int capacity;
};
LFU缓存
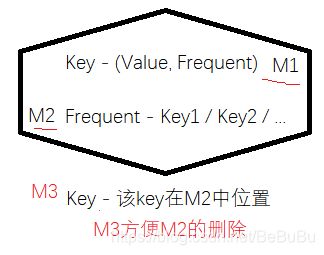
LRU算法是首先淘汰最长时间未被使用的页面,而LFU是先淘汰一定时间内被访问次数最少的页面(频率)
图示map:
class LFUCache {
public:
LFUCache(int capacity) : capacity(capacity), min_freq(0) {
}
int get(int key) {
if (this->H.find(key) == this->H.end()) return -1;
int pre_freq = this->H[key].first++;
this->L[pre_freq + 1].splice(this->L[pre_freq + 1].begin(), \
this->L[pre_freq], this->R[key]);
if (this->L[min_freq].empty()) min_freq++;
if (this->L[pre_freq].empty()) this->L.erase(pre_freq);
return this->H[key].second;
}
void put(int key, int value) {
if (this->get(key) != -1) {
this->H[key].second = value;
return;
}
if (this->H.size() >= capacity) {
auto& tmp_key_list = this->L[this->min_freq];
this->H.erase(tmp_key_list.back());
this->R.erase(tmp_key_list.back());
if (tmp_key_list.size() > 1) tmp_key_list.pop_back();
else this->L.erase(this->min_freq);
}
this->H[key] = {1, value};
this->L[1].emplace_front(key);
this->R[key] = this->L[1].begin();
this->min_freq = 1;
}
private:
unordered_map<int, pair<int, int>> H; // key-(freq, value)
unordered_map<int, list<int>> L; // freq-[key]s
unordered_map<int, list<int>::iterator> R; // key-freq_list_iter
int capacity, min_freq;
};
单调栈&单调队列
单调栈 Monotonic Stack
每次新元素入栈后,栈内的元素都保持有序(单调递增或单调递减)
单调栈用途不太广泛,只处理一种典型的问题,叫做 Next Greater Element
Next Greater Element 暴力法是 O(n^2) 有三道题 Leetcode 496 503 556
L739 每日温度
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
int n = temperatures.size();
vector<int> res(n, 0);
stack<int> st; // 单减栈
for (int i = 0; i < temperatures.size(); ++i) {
while (!st.empty() && temperatures[i] > temperatures[st.top()]) {
auto t = st.top(); st.pop();
res[t] = i - t;
}
st.push(i);
}
return res;
}
};
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& T) {
vector<int> res(T.size(),0);
stack<int> s; // 单增栈
for (int i = T.size() - 1; i >= 0; --i) {
while (!s.empty() && T[s.top()] <= T[i]) s.pop();
res[i] = s.empty() ? 0 : (s.top() - i);
s.push(i);
}
return res;
}
};
496 下一个更大的数
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
哈希表+单调栈 解法!
class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
vector<int> r;
unordered_map<int,int> m;
stack<int> s;
for (auto& n : nums2) {
while (!s.empty() && n > s.top()) {
int x = s.top(); s.pop();
m[x] = n;
}
s.push(n);
}
for (auto& n : nums1)
r.push_back(m.count(n) ? m[n] : -1);
return r;
}
};
503 下一个更大的数 (循环)
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
int n = nums.size();
vector<int> res(n,-1);
stack<int> s;
for (int i = 2*n-1; i >= 0; i--) {
while (!s.empty() && nums[i%n] >= s.top()) s.pop();
res[i%n] = s.empty()?-1:s.top();
s.push(nums[i%n]);
}
return res;
}
};
556 下一个更大数(单个数)
这道题没用到单调栈
class Solution {
public:
int nextGreaterElement(int n) {
string str = to_string(n);
if (str.size() < 2) return -1;
// step 1
int i = str.size() - 1;
for (; i > 0; i--) if (str[i - 1] < str[i]) break;
if (i < 1) return -1;
// step 2
int min_max = this->find_min_max(str, i, str.size(), str[i - 1]);
swap(str[min_max], str[i - 1]);
// step 3
sort(str.begin() + i, str.end());
long rvl = stol(str);
return rvl > INT_MAX ? -1 : rvl;
}
int find_min_max(const string& str, int s, int e, char r) {
int m = s;
while (s < e) {
m = (s + e) / 2;
if (str[m] > r) {
s = m + 1;
} else {
e = m;
}
}
return str[m] > r ? m : m - 1;
}
};
class Solution {
public:
int nextGreaterElement(int n) {
string n_str = to_string(n);
int N = n_str.size(), i = N - 1;
for (; i > 0; --i) if (n_str[i] > n_str[i-1]) break;
if (i == 0) return -1;
sort(n_str.begin()+i, n_str.end());
for (int j = i; j < N; ++j) {
if (n_str[j] > n_str[i-1]) {
swap(n_str[j], n_str[i-1]);
break;
}
}
long res = stol(n_str);
return res >= INT_MAX ? -1 : res;
}
};
402 移掉k位数字
- 给定一个以字符串表示的非负整数 num,移除这个数中的 k 位数字,使得剩下的数字最小
class Solution {
public:
string removeKdigits(string num, int k) {
string rvl;
int n = num.size() - k;
if (n < 1) return "0";
for (int i = 0; i < num.size(); i++) {
while (k > 0 && !rvl.empty() && rvl.back() > num[i]) {
rvl.pop_back();
k--;
}
rvl.push_back(num[i]);
}
rvl = rvl.substr(0, n);
rvl.erase(0, rvl.find_first_not_of("0"));
return rvl.empty() ? "0" : rvl;
}
};
316 去除重复字母
- 给你一个仅包含小写字母的字符串,请你去除字符串中重复的字母,使得每个字母只出现一次
- 需保证返回结果的字典序最小(要求不能打乱其他字符的相对位置)
class Solution {
public:
string removeDuplicateLetters(string s) {
string st;
size_t i = 0;
for (size_t i = 0; i < s.size(); i++) {
if (st.find(s[i]) != string::npos) continue;
// st.back()大且字符串后面还会出现
while (!st.empty() && st.back() > s[i] &&
s.find(st.back(), i) != string::npos)
st.pop_back();
st.push_back(s[i]);
}
return st;
}
};
321 拼接最大数
- 给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字
- 现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数,要求从同一个数组中取出的数字保持其在原数组中的相对顺序。
class Solution {
public:
bool dictOrderBigger(vector<int>& nums1, int s1, vector<int>& nums2, int s2) { // 判断字典序
for (int i = s1, j = s2; i < nums1.size() && j < nums2.size(); i++, j++) {
if (nums1[i] > nums2[j]) return true;
if (nums1[i] < nums2[j]) return false;
}
return nums1.size() - s1 > nums2.size() - s2;
}
vector<int> maxNumber(vector<int>& nums, int k) {
vector<int> rvl; // 单调栈取最大字典序
int dk = nums.size() - k;
if (dk < 0) return {};
for (int i = 0; i < nums.size(); i++) {
while (dk > 0 && !rvl.empty() && rvl.back() < nums[i]) {
rvl.pop_back();
dk--;
}
rvl.push_back(nums[i]);
}
return vector<int>(rvl.begin(), rvl.begin() + k);
}
vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size(), m = nums2.size(); // 两个数组融合成最大字典序
vector<int> rvl(n + m, 0);
int i = 0, j = 0, k = 0;
while (i < n || j < m) {
if (i >= n) rvl[k++] = nums2[j++];
else if (j >= m) rvl[k++] = nums1[i++];
else if (dictOrderBigger(nums1, i, nums2, j)) rvl[k++] = nums1[i++];
else rvl[k++] = nums2[j++];
}
return rvl;
}
vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {
vector<int> rvl(k, 0);
int n = nums1.size(), m = nums2.size();
for (int i = 0; i <= k; i++) {
if (i > n || k - i > m) continue;
auto x = maxNumber(nums1, i);
auto y = maxNumber(nums2, k - i);
auto z = maxNumber(x, y);
if (dictOrderBigger(z, 0, rvl, 0)) rvl = z;
}
return rvl;
}
};
单调队列
解决滑动窗的一系列问题!
L239 滑动窗口最大值
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
| 滑动窗口的位置 | 最大值 |
|---|---|
| [1 3 -1] -3 5 3 6 7 | 3 |
| 1 [3 -1 -3] 5 3 6 7 | 3 |
| 1 3 [-1 -3 5] 3 6 7 | 5 |
| 1 3 -1 [-3 5 3] 6 7 | 5 |
| 1 3 -1 -3 [5 3 6] 7 | 6 |
| 1 3 -1 -3 5 [3 6 7] | 7 |
| 1 队列有两个操作push+pop; 单调队列有三个push+pop+max | |
| 2 单调队列的 push 方法依然在队尾添加元素,但是要把前面比新元素小的元素都删掉 即头处即最大值! | |
| 具体代码如下: |
class Solution {
private:
class Xqueue { // 从头到尾单减
private:
deque<int> deq;
public:
void push(int num) {
while (!deq.empty() && deq.back() < num)
deq.pop_back();
deq.push_back(num);
}
void pop(int num) {
if (!deq.empty() && deq.front() == num)
deq.pop_front();
}
int max() {
return deq.front();
}
};
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
Xqueue que;
vector<int> res;
for (int i = 0; i < nums.size(); ++i) {
if (i < k - 1) que.push(nums[i]);
else {
que.push(nums[i]);
res.push_back(que.max());
que.pop(nums[i-k+1]);
}
}
return res;
}
};
有序表 Ordered map
855. 考场就座
先看 849到最近的人的最大距离 这道题!方便理解题目!
849 到最近人的最大距离
输入:[1,0,0,0,1,0,1]
输出:2
解释:
如果亚历克斯坐在第二个空位(seats[2])上,他到离他最近的人的距离为 2 。
如果亚历克斯坐在其它任何一个空位上,他到离他最近的人的距离为 1 。
因此,他到离他最近的人的最大距离是 2 。
双指针法!!!
class Solution {
public:
int maxDistToClosest(vector<int>& seats) {
int res = 0, start = 0;
int N = seats.size();
for (int i = 0; i < N; ++i) {
if (seats[i]==0) continue;
if (start == 0) res = max(res, i - start); // 0001
else res = max(res, (i - start + 1) / 2); // 10001
start = i + 1;
}
return max(res, N-start); // 1000
}
};
拓展:855 考生就坐
当学生进入考场后,他必须坐在能够使他与离他最近的人之间的距离达到最大化的座位上。如果有多个这样的座位,他会坐在编号最小的座位上。(另外,如果考场里没有人,那么学生就坐在 0 号座位上。)
- 将连续空位抽象为线段,找到最长的线段
- 但凡遇到在动态过程中取最值的要求,肯定要使用有序数据结构
- 需要有序MAP,要么二叉堆要么红黑树,二叉堆实现的优先级队列取最值的时间复杂度是 O(logN),但是只能删除最大值。平衡二叉树也可以取最值,也可以修改、删除任意一个值,而且时间复杂度都是 O(logN)。
- JAVA中的TreeSet就是红黑树实现的有序集合,即C++中的set数据结构!
- 首先我们还是借用 849 思想,使用一维数组来实现,然后进行优化,使用set结构以通过OJ!
W1 一维数组类型
超过时间限制!!!
class ExamRoom {
private:
vector<int> seats;
public:
ExamRoom(int N) { seats.resize(N,0); }
void leave(int p) {
seats[p] = 0;
}
int seat() {
int start = 0, len = 0, pos = start;
int N = seats.size();
for (int i = 0; i < N; ++i) {
if (seats[i] == 0) continue;
if (start == 0) len = max(len, i - start);
else {
if (len < (i - start + 1) / 2) {
len = (i - start + 1) / 2;
pos = start + len - 1;
}
}
start = i + 1;
}
if (start != 0 && len < N - start) {
len = N - start;
pos = N - 1;
}
seats[pos] = 1;
return pos;
}
};
W2 有序set类型
class ExamRoom {
private:
set<int> fullSeats;
int N;
public:
ExamRoom(int N) : N(N) { }
void leave(int p) {
fullSeats.erase(p);
}
int seat() {
int start = 0, len = 0, pos = start;
for (auto x : fullSeats) {
if (start == 0) len = max(len, x - start);
else {
if (len < (x - start + 1) / 2) {
len = (x - start + 1) / 2;
pos = start + len - 1;
}
}
start = x + 1;
}
if (start != 0 && len < N - start) {
len = N - start;
pos = N - 1;
}
fullSeats.emplace(pos);
return pos;
}
};
栈
括号合法性
L20 三种括号组成的字符串,判断是否合法 {} [] ()
单种括号的情况
class Solution {
public:
bool isValid(string s) {
int left = 0;
for (auto& c : s) {
if (c == '(') left++;
else if (c == ')') left--;
if (left < 0) return false;
}
return true;
}
};
上述方法不能直接用于三种括号的检测,因为存在“ ([)] ” 这种非法情况。
多括号 - 栈方法
class Solution {
public:
bool isValid(string s) {
stack<char> st;
for (auto& c : s) {
if (c == '(' || c == '{' || c == '[')
st.push(c);
else {
if (st.empty()) return false;
char t = st.top(); st.pop();
if (c != retMatcher(t)) return false;
}
}
return st.empty();
}
char retMatcher(char x) {
if (x == '(') return ')';
else if (x == '[') return ']';
else return '}';
}
};
队列
XX
BFS
链表
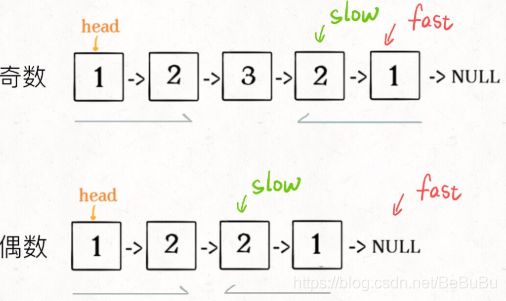
回文链表
回文串和回文序列相关
寻找回文串的核心思想是从中心向两端扩展:
判断一个字符串是不是回文串就简单很多,不需要考虑奇偶情况,只需要「双指针技巧」,从两端向中间逼近即可:
bool isPalindrome(string s) {
int left = 0, right = s.length - 1;
while (left < right) {
if (s[left] != s[right])
return false;
left++; right--;
}
return true;
}
- 寻找回文串是从中间向两端扩展,判断回文串是从两端向中间收缩。
- 对于单链表,无法直接倒序遍历,可以造一条新的反转链表,可以利用链表的后序遍历,也可以用栈结构倒序处理单链表。
链表的后序遍历 O(n)空间复杂
和堆栈法一个复杂度!
启发:
二叉树的遍历:
void traverse(TreeNode root) {
// 前序遍历代码
traverse(root.left);
// 中序遍历代码
traverse(root.right);
// 后序遍历代码
}
==> 链表的遍历:
void traverse(ListNode head) {
// 前序遍历代码
traverse(head.next);
// 后序遍历代码
}
class Solution {
public:
bool isPalindrome(ListNode* head) {
ListNode *right = head, *left = head;
return posOrder(right, left);
}
bool posOrder(ListNode* right, ListNode*& left) {
// left 引用
if (!right) return true;
bool res = posOrder(right->next, left);
res = res && (right->val == left->val);
left = left->next;
return res;
}
};
快慢指针+反转
class Solution {
public:
bool isPalindrome(ListNode* head) {
ListNode *slow = head, *fast = head;
ListNode *p = head, *q = head;
while (fast != NULL && fast->next != NULL) {
p = slow; //恢复1
slow = slow->next;
fast = fast->next->next;
}
// 链表长度奇 slow还要再前进一步
if (fast) {
slow = slow->next;
p = p->next;
}
ListNode *left = head;
ListNode *right = reverse(slow);
q = right; // 恢复2
while (right) {
if (left->val != right->val) return false;
left = left->next;
right = right->next;
}
// 恢复原链表
// p: slow前面; q:反转链表的头!
if (p && q) p->next = reverse(q);
return true;
}
private:
ListNode* reverse(ListNode* node) {
ListNode *pre = NULL, *cur = node;
while (cur) {
ListNode *next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
};
206 反转列表
反转链表 正常 / 部分/ k个一组
W1 双指针法
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode *pre = NULL, *cur = head;
while (cur) {
ListNode* next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
};
W2 递归法
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (!head) return head;
if (!head->next) return head;
ListNode* last = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return last;
}
};
92 反转m~n间的链表
先反转前k节点,图示如下:
W1 递归
class Solution {
public:
ListNode *successor = NULL;
ListNode* reverseL(ListNode *head, int k) {
if (k == 1) {
successor = head->next;
return head;
}
ListNode *last = reverseL(head->next, k-1);
head->next->next = head;
head->next = successor;
return last;
}
ListNode* reverseBetween(ListNode *head, int m, int n) {
if (m == n) return head;
if (m == 1) return reverseL(head, n);
head->next = reverseBetween(head->next, m-1, n-1);
return head;
}
};
W2 迭代
四个指针:pre:m-1 start:m end:n next:n+1
在206迭代法基础上!
class Solution {
public:
ListNode* reverse(ListNode *head) {
ListNode *pre = NULL, *cur = head;
while (cur) {
ListNode *next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
ListNode* reverseBetween(ListNode* head, int m, int n) {
ListNode* dummy = new ListNode(0);
dummy->next = head;
ListNode *pre = dummy, *next = dummy;
ListNode *start = dummy, *end = dummy;
int cnt1 = m, cnt2 = n;
while (--cnt1) pre = pre->next;
while (cnt2--) end = end->next;
start = pre->next;
next = end->next;
end->next = NULL;
ListNode* X = reverse(start);
ListNode* Y = pre->next;
pre->next = X;
Y->next = next;
return dummy->next;
}
};
25 K个一组反转链表
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if (!head) return NULL;
ListNode *x = head, *y = head;
for (int i = 0; i < k; ++i) {
if (!y) return head;
y = y->next;
}
ListNode *newN = reverse(x, y);
x->next = reverseKGroup(y, k);
return newN;
}
ListNode* reverse(ListNode* left, ListNode* right) {
// left...right-1 反转
if (left == right) return left;
ListNode* pre = NULL, *cur = left;
while (cur != right) {
ListNode *next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
};
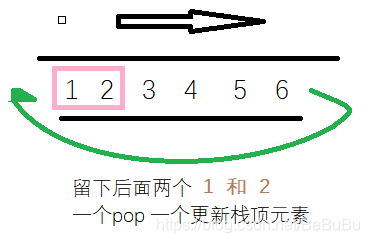
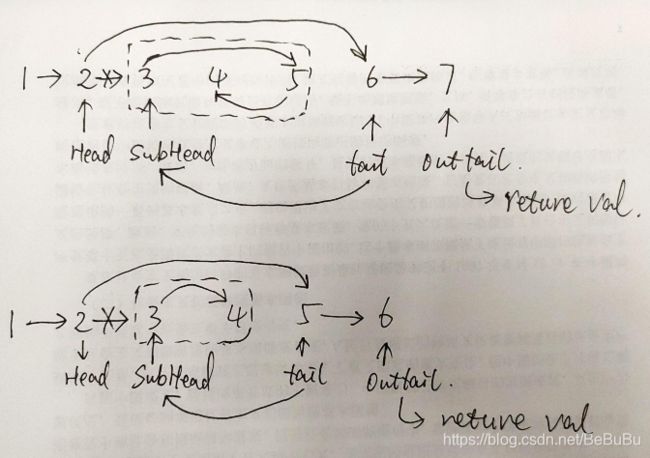
143 重排链表
// DFS
void reorderList(ListNode* head) {
if (!head || !head->next || !head->next->next)
return;
int len = 0;
ListNode *h = head;
while (h) {len++; h = h->next;}
dfs(head, len);
}
ListNode *dfs(ListNode *head, int len) {
if (len == 1) {
ListNode *outTail = head->next;
head->next = NULL;
return outTail;
}
if (len == 2) {
ListNode *outTail = head->next->next;
head->next->next = NULL;
return outTail;
}
ListNode *tail = dfs(head->next, len - 2);
ListNode *subHead = head->next;
head->next = tail;
ListNode *outTail = tail->next;
tail->next = subHead;
return outTail;
}
- 链表存储
// 线性表记录
void reorderList(ListNode* head) {
if (!head) return;
vector<ListNode*> H;
while (head) {
H.push_back(head);
head = head->next;
}
int i = 0, j = H.size() - 1;
while (i < j) {
H[i++]->next = H[j];
if (i == j) break;
H[j--]->next = H[i];
}
H[i]->next = NULL;
}
- 反转 + 快慢指针
// 快慢指针 + 反转
void reorderList(ListNode* head) {
if (!head || !head->next || !head->next->next)
return;
ListNode *slow = head, *fast = head;
while (fast->next && fast->next->next) {
slow = slow->next;
fast = fast->next->next;
}
ListNode *newHead = slow->next;
slow->next = NULL;
newHead = reverse(newHead);
while (newHead) {
ListNode *t = newHead->next;
newHead->next = head->next;
head->next = newHead;
head = newHead->next;
newHead = t;
}
}
ListNode *reverse(ListNode *node) {
if (!node) return NULL;
ListNode *cur = node, *pre = NULL;
while (cur) {
ListNode *next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
树
树的搜索框架,先中后三序,加之中间计算和中间状态的保存!
二叉树遍历
前序遍历(迭代)
- 递归 略
- 迭代:压栈先右后左
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
st.push(root);
while (!st.empty()) {
TreeNode *cur = st.top(); st.pop();
if (cur) {
res.push_back(cur->val);
st.push(cur->right);
st.push(cur->left);
}
}
return res;
}
};
中序遍历(迭代)
- 递归 略
- 迭代:压栈一直压左,push完了压右
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
TreeNode *p = root;
while (p || !st.empty()) {
while (p) {
st.push(p);
p = p->left;
}
TreeNode *cur = st.top(); st.pop();
res.push_back(cur->val);
p = cur->right;
}
return res;
}
};
后序遍历(迭代)
- 递归 略
- 迭代:先左后右压栈,反转输出
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
st.push(root);
while (!st.empty()) {
TreeNode *cur = st.top(); st.pop();
if (cur) {
res.push_back(cur->val);
st.push(cur->left);
st.push(cur->right);
}
}
reverse(res.rbegin(), res.rend());
return res;
}
};
- 上面这种遍历并不能保证每次访问是按照后序遍历来的,而是反转!所以采用下面这种迭代代码(
所有迭代遍历中最难的): - 遍历顺序
左右中,在右节点空或者右节点是上一个遍历到的节点的时候,才把当前节点push进res,就是先把子节点全部存下之后才放父节点 保证了先子后父,且是先遍历左节点,即内部的 “左到头” 的栈push,保证了先左后右
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
TreeNode *cur = root, *pre = NULL;
while (cur || !st.empty()) {
while (cur) { // 左到头
// "先左后右"
st.push(cur);
cur = cur->left;
}
if (!st.empty()) {
cur = st.top(); st.pop();
if (!cur->right || pre == cur->right) {
// "先子后父"
res.push_back(cur->val);
pre = cur;
cur = NULL;
} else { // 存右
st.push(cur);
cur = cur->right;
}
}
}
return res;
}
};
二叉树前序+中序遍历 > 后序
- 不建树
#include 完全二叉树
满二叉树,每个非叶节点都有两个子节点!
完全二叉树,紧凑靠左排列。完全的含义则是最后一层没有满,并没有满。
L222 求完全二叉树的节点数
普通的就遍历加1就行:
public int countNodes(TreeNode root) {
if (root == null) return 0;
return 1 + countNodes(root.left) + countNodes(root.right);
}
满二叉树,先找到高度,然后2^h-1就是节点数!
public int countNodes(TreeNode root) {
int h = 0;
// 计算树的高度
while (root != null) {
root = root.left;
h++;
}
// 节点总数就是 2^h - 1
return (int)Math.pow(2, h) - 1;
}
而完全二叉树是由一半满一半完全构成:
所以可以有O(lgn*lgn)复杂度!
class Solution {
public:
int countNodes(TreeNode* root) {
TreeNode *left_n = root, *right_n = root;
int left = 0, right = 0;
while (left_n) {
left_n = left_n->left;
left++;
}
while (right_n) {
right_n = right_n->right;
right++;
}
if (left == right) return pow(2,left)-1;
return 1 + countNodes(root->left) + countNodes(root->right);
}
};
二叉搜索树
左子树<根节点<右子树,即按中序遍历数会得到升序排列!
BST的 判断/增/删/查
- 二叉树算法设计的总路线:把当前节点要做的事做好,其他的交给递归框架,不用当前节点操心。
- 如果当前节点会对下面的子节点有整体影响,可以通过辅助函数增长参数列表,借助参数传递信息。
- 在二叉树框架之上,扩展出一套 BST 遍历框架:
void BST(TreeNode root, int target) {
if (root.val == target)
// 找到目标,做点什么
if (root.val < target)
BST(root.right, target);
if (root.val > target)
BST(root.left, target);
}
- 掌握了 BST 的基本操作。
判断
L98 判断是否是BST,
W1 递归法
class Solution {
public:
bool isValidBST(TreeNode* root) {
return dfs(root, LONG_MIN, LONG_MAX);
}
bool dfs(TreeNode* node, long left_max, long right_min) {
if (!node) return true;
if (left_max >= node->val || right_min <= node->val) return false;
return dfs(node->left, left_max, node->val) &&
dfs(node->right, node->val, right_min);
}
};
W2 中序遍历法
class Solution {
public:
bool isValidBST(TreeNode* root) {
long pre = LONG_MIN;
return inorder(root, pre);
}
bool inorder(TreeNode* node, long& preV) {
// 必须是引用!否则记录不了prev, 最上层仍然是LONG_MIN
if (!node) return true;
if (!inorder(node->left, preV)) return false;
if (preV >= node->val) return false;
preV = node->val;
return inorder(node->right, preV);
}
};
PS: 中序遍历可以用栈实现,就头节点开始,循环导入左节点,再取一个处理弹出,导入右节点及其循环左节点:
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> s;
TreeNode *p = root, *pre = NULL;
while (p || !s.empty()) {
while (p) {
s.push(p);
p = p->left;
}
p = s.top(); s.pop();
if (pre && p->val <= pre->val) return false;
pre = p;
p = p->right;
}
return true;
}
};
查询
BST遍历框架
boolean isInBST(TreeNode root, int target) {
if (root == null) return false;
if (root.val == target)
return true;
if (root.val < target)
return isInBST(root.right, target); // 搜索右子树
if (root.val > target)
return isInBST(root.left, target); // 搜索左子树
}
插入
延续遍历框架,修改如下:
TreeNode insertIntoBST(TreeNode root, int val) {
// 找到空位置插入新节点
if (root == null) return new TreeNode(val);
// if (root.val == val)
// BST 中一般不会插入已存在元素
if (root.val < val)
root.right = insertIntoBST(root.right, val);
if (root.val > val)
root.left = insertIntoBST(root.left, val);
return root;
}
删除
TreeNode deleteNode(TreeNode root, int key) {
if (root.val == key) {
// 找到啦,进行删除
} else if (root.val > key) {
root.left = deleteNode(root.left, key);
} else if (root.val < key) {
root.right = deleteNode(root.right, key);
}
return root;
}
而如何删掉元素而不破坏BST性质才算重点!
待删除的节点可能有三种情况:
1 为叶节点,直接删掉
2 一个子节点,用子节点替换就行
3 两个子节点,找到最大左节点或最小右节点替换即可
实现代码如下:
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (!root) return root;
if (root->val == key) {
if (!root->left || !root->right)
return (root->left) ? root->left : root->right;
int right_min = getMin(root->right);
root->val = right_min;
root->right = deleteNode(root->right, right_min);
}
else if (root->val < key) root->right = deleteNode(root->right, key);
else if (root->val > key) root->left = deleteNode(root->left, key);
return root;
}
private:
int getMin(TreeNode* node) { // BST搜索最小值: 找最左子节点
int m = node->val;
while (node->left) {
node = node->left;
m = node->val;
}
return m;
}
};
PS:这个删除操作并不完美,因为我们一般不会通过 root.val = minNode.val 修改节点内部的值来交换节点,而是通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点。因为具体应用中,val 域可能会很大,修改起来很耗时,而链表操作无非改一改指针,而不会去碰内部数据。
简化一点代码:
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (!root) return NULL;
if (root->val == key) {
if (!root->right) return root->left;
else {
TreeNode *cur = root->right;
while (cur->left) cur = cur->left;
swap(root->val, cur->val);
}
}
root->left = deleteNode(root->left, key);
root->right = deleteNode(root->right, key);
return root;
}
};
99 二叉搜索树恢复
BST: 左 < 根 < 右
二叉树的中序遍历,保持节点递增!
W1 DFS
class Solution {
public:
void recoverTree(TreeNode* root) {
inordersearch(root);
swap(w1->val, w2->val);
}
void inordersearch(TreeNode* node) {
if (!node) return;
inordersearch(node->left);
if (!pre) pre = node; // 到中序遍历的起始处赋值pre
if (node->val < pre->val) {
w1 = (w1 == NULL) ? pre : w1;
w2 = node;
}
pre = node;
inordersearch(node->right);
}
private:
TreeNode *w1, *w2, *pre;
};
W2 Stack
Binary Tree Inorder Traversal 也可以借助栈来实现
W3 Morris遍历 方法 O(1)空间复杂度
线索二叉树
下面是不破坏树结构:
好好学!
// Now O(1) space complexity
class Solution {
public:
void recoverTree(TreeNode* root) {
TreeNode *first = nullptr, *second = nullptr, *cur = root, *pre = nullptr ;
while (cur) {
if (cur->left){
TreeNode *p = cur->left;
while (p->right && p->right != cur) p = p->right;
if (!p->right) {
p->right = cur;
cur = cur->left;
continue;
} else {
p->right = NULL;
}
}
if (pre && cur->val < pre->val){
if (!first) first = pre;
second = cur;
}
pre = cur;
cur = cur->right;
}
swap(first->val, second->val);
}
};
255 判断数组是不是二叉搜索树的前序遍历
- 是类似于数的中序遍历的框架,栈是单减栈,一直要压完 左子树!
- temp存的是 理论上 左子树 的最小值,如果这个最小值大于了 当前处理的值
- 那就不是BST树的Preorder Vector!
class Solution {
public:
bool verifyPreorder(vector<int>& preorder) {
if (!preorder.size()) return true;
stack<int> s;
s.push(preorder[0]);
int temp = -1e10;
for (int i=1;i<preorder.size();i++)
{
if (preorder[i] < temp) return false;
while(!s.empty() && preorder[i] > s.top())
{ // 看数组 preorder 是不是已经到了某个根节点的 右子树了
temp=s.top();
s.pop();
}
s.push(preorder[i]);
}
return true;
}
};
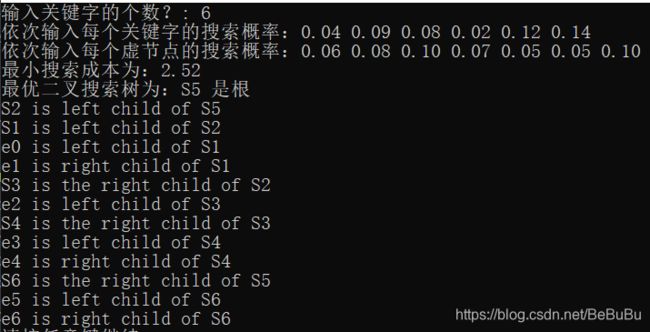
最优二叉搜索树
- Optimal Binary Search Tree,OBST
- 搜索成本最低的BST,即平均比较次数最小
- OBST 的性质:一个树是OBST,那么其左子树和右子树都是OBST
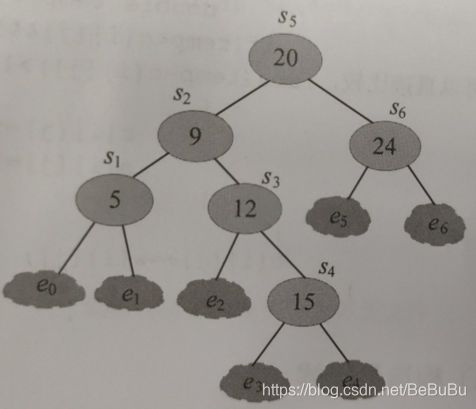
- 定义问题: c [ i ] [ j ] c[i][j] c[i][j] 表示 s i , s i + 1 , . . . , s j {s_i, s_{i+1}, ..., s_j} si,si+1,...,sj 和 e i − 1 , e i , . . . , e j {e_{i-1}, e_i, ..., e_{j}} ei−1,ei,...,ej 构成的 最优二叉 搜索树 的 搜索成本!(节点 i i i 到节点 j j j)
- 其中 s s s 表示搜索成功 的成本, e e e表示 搜索失败 的成本
- 又有把 s s s 称为关键字 搜索概率, e e e 称为虚节点 搜索概率!
- 设 k k k 为根节点,{ e i − 1 , s i , e i , s i + 1 , . . . , ( s k , e k ) , . . . s j , e j e_{i-1}, s_i, e_i, s_{i+1}, ..., (s_k, e_k), ... s_j, e_{j} ei−1,si,ei,si+1,...,(sk,ek),...sj,ej}
- 最优值 递归 式子: S [ i ] [ j ] S[i][j] S[i][j] 表示 最优解 C [ i ] [ j ] C[i][j] C[i][j]的最优策略位置!
- { 0 0 j = i − 1 min i ≤ k ≤ j , o r , s [ i ] [ j − 1 ] ≤ k ≤ s [ i + 1 ] [ j ] { c [ i ] [ k − 1 ] + c [ k + 1 ] [ j ] } + w [ i ] [ j ] j ≥ i w [ i ] [ j ] = { e i − 1 j = i − 1 w [ i ] [ j − 1 ] + s j + e j j ≥ i \left\{\begin{array}{c} 0 \quad 0 \quad j=i-1 \\ \min _{i \leq k \leq j, o r, s[i][j-1] \leq k \leq s[i+1][j]}\{c[i][k-1]+c[k+1][j]\}+w[i][j] \quad j \geq i \\ w[i][j]=\left\{\begin{array}{cc} e_{i-1} & j=i-1 \\ w[i][j-1]+s_{j}+e_{j} & j \geq i \end{array}\right. \end{array}\right. ⎩ ⎨ ⎧00j=i−1mini≤k≤j,or,s[i][j−1]≤k≤s[i+1][j]{c[i][k−1]+c[k+1][j]}+w[i][j]j≥iw[i][j]={ei−1w[i][j−1]+sj+ejj=i−1j≥i
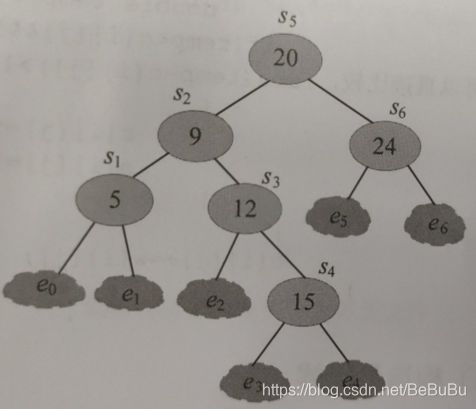
- 代码:
#include 124 计算二叉树的最大路径和
class Solution {
public:
int maxPathSum(TreeNode* root) {
int res = INT_MIN;
oneSideMax(root, res);
return res;
}
int oneSideMax(TreeNode* root, int& res) {
if (!root) return 0;
int leftMax = max(0,oneSideMax(root->left, res)); // 取正路径
int rightMax = max(0,oneSideMax(root->right, res));
res = max(res, leftMax+rightMax+root->val); // 历史最大值
return max(leftMax, rightMax) + root->val;
}
};
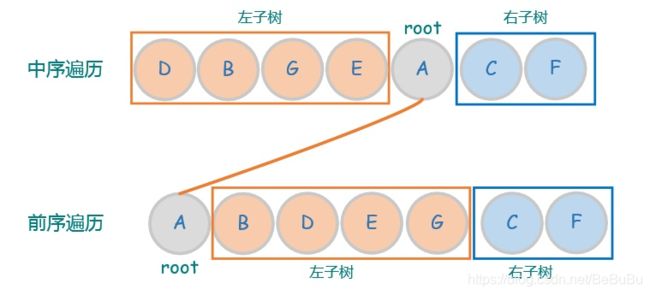
105&106 二叉树还原
先序 根左右 中序 左根右 后序 左右根
还原需要先序+中序,或中序+后序
先序+后序不能还原,如先序 AB 后序 BA, 不能确认B是A的左节点还是右节点
W1 105 先序+中序
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return splitConstruct(preorder, inorder,
0, preorder.size()-1, 0, inorder.size()-1);
}
TreeNode* splitConstruct(
vector<int>& prev, vector<int>& inv,
int pre1, int pre2, int in1, int in2) {
if (pre1 > pre2 || in1 > in2) return NULL;
TreeNode* t = new TreeNode(prev[pre1]);
int i = in1 - 1;
while (inv[++i] != t->val && i <= in2);
int left_len = i - in1;
t->left = splitConstruct(prev,inv,pre1+1,pre1+left_len,in1,i-1);
t->right= splitConstruct(prev,inv,pre1+left_len+1,pre2,i+1,in2);
return t;
}
};
W2 106 中序+后序
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return splitConstructor(inorder,0,inorder.size()-1,
postorder,0,postorder.size()-1);
}
TreeNode* splitConstructor(vector<int>& inorder, int in1, int in2,
vector<int>& postorder, int po1, int po2) {
if (in1 > in2 || po1 > po2) return NULL;
TreeNode* t = new TreeNode(postorder[po2]);
int i = in1-1;
while (inorder[++i]!=t->val && i <= in2);
int left_len = i - in1;
t->left = splitConstructor(inorder,in1,i-1,postorder,po1,po1+left_len-1);
t->right = splitConstructor(inorder,i+1,in2,postorder,po1+left_len,po2-1);
return t;
}
};
W3 889 前序+后序,返回其中一个可能的树序列
class Solution {
public:
TreeNode* constructFromPrePost(vector<int>& pre, vector<int>& post) {
return helper(pre, 0, pre.size() - 1, post, 0, post.size() - 1);
}
TreeNode* helper(vector<int>& pre, int x0, int x1,
vector<int>& post, int y0, int y1) {
if (x0 > x1 || y0 > y1 || pre[x0] != post[y1]) return NULL;
TreeNode* root = new TreeNode(pre[x0]);
if (x0 == x1) return root;
int L = y0;
for (int i = y0; i < y1; i++)
if (post[i] == pre[x0 + 1])
L = i;
L -= y0;
root->left = helper(pre, x0 + 1, x0 + L + 1, post, y0, y0 + L);
root->right = helper(pre, x0 + L + 2, x1, post, y0 + L + 1, y1 - 1);
return root;
}
};
红黑树 / RBT
- STL的关联容器(map、set、multimap、multiset)底层都是基于红黑树(Red Black Tree,RBT)来实现的,红黑树是一种被广泛使用的二叉查找树(Binary Search Tree,BST),有比较良好的操作效率。
- 平衡二叉树定义:一棵空树或它的任意节点的左右两个子树的高度差的绝对值均不超过1。
- 红黑树是一颗二叉搜索树,它在每个节点上增加了一个存储位来表示节点的颜色,可以是red或black。通过对任何一条从根节点到叶子节点的简单路径上的颜色来约束,红黑树保证了最长路径不超过最短路经的两倍,因此近似于平衡。
(1) 每个节点或者是黑色,或者是红色;根节点是黑色;每个叶子节点是黑色 [注意:这里叶子节点,是指为空的叶子节点!];
(2) 如果一个节点是红色的,则它的子节点必须是黑色的;
(3) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点; - (3)确保没有一条路径会比其他路径长出俩倍。因此红黑树是相对是接近平衡的二叉树

旋转
增加
删除
数组中树的思想
最大/最小堆
- 描述父节点和两个子节点之间的大小关系,0,1,2,3… 节点表示,
i节点的左节点下标为2i + 1, 右节点2i + 2使用STL的 priority_queue 表示
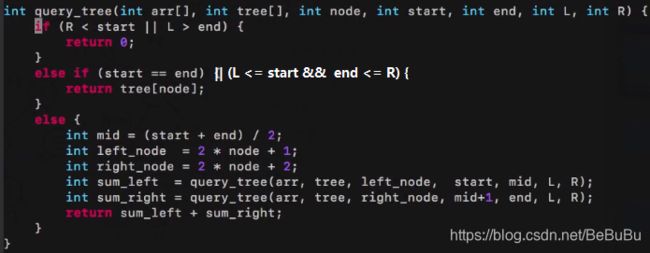
二叉索引树/ 树状数组 Binary Indexed Tree
| 更新 \ 查询 | 多个 | 单个 |
|---|---|---|
| 多个(区间) | 区间更新 区间查询 | 区间更新 单点查询 |
| 单个 | 单点更新 区间查询 | 单点更新 单点查询 |
- 树状数组提供一种从树的思路 管理 前缀和或差分,树是抽象出来的,操作的还是数组

- i节点 C [ i ] C[i] C[i] 的 父节点为 C [ i + 2 k ] C[i + 2^k] C[i+2k] ,兄弟节点为 C [ i − 2 k ] C[i - 2^k] C[i−2k]
- 单点更新单点查询,普通数据即可
- 单点更新区间查询,维护的是原数组的关系,如上图

- 区间更新单点查询,需要维护的是原数组的差分数组,因为差分数组可以将 区间更新转变为单点更新
例子, 1 , 2 , 3 , 4 , 5 = > 1 , 1 , 1 , 1 , 1 1,2,3,4,5 => 1,1,1,1,1 1,2,3,4,5=>1,1,1,1,1, 更新区间 [ 3 , 4 ] [3,4] [3,4] + 1,更新差分数组为 1 , 1 , [ 2 ] , 1 , [ 0 ] 1,1,[2],1,[0] 1,1,[2],1,[0] - 区间更新区间查询,需要维护两个树状数组!如下图中的 n D [ i ] nD[i] nD[i] 和 D [ i ] ∗ ( i − 1 ) D[i] * (i - 1) D[i]∗(i−1)
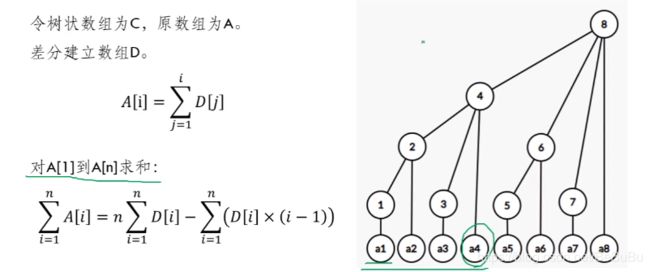
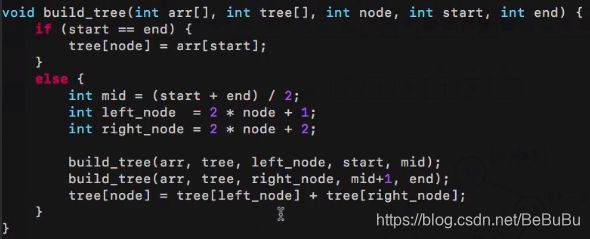
线段树 Segment Tree
-
解决的是 区间的 可加性问题!如区间众数 树 就不可行!而最值和均值 从区间角度上是 “可加的”
-
结构上,原数组元素存在于 叶节点(和树状数组的结构不同),相同于 堆 的下标编码方式, r o o t : i > ( l e f t : 2 i + 1 , r i g h t : 2 i + 2 ) root: i>(left: 2i+1, right: 2i+2) root:i>(left:2i+1,right:2i+2),序列数组长度 n n n的话,需要开 4 n 4n 4n大小的数组(每个节点存下标和 维护的值(最值等))
-
即把数组按照堆的方式编码,父节点负责其为根的 子树 的属性统计 区间性质
-
权值线段树,维护的是 该数出现的次数
-
ZKW线段树
离散化
- 适用范围:数组中元素数值很大,但个数不是很多。比如将a[]=[1,3,100,2000,500000]映射到[0,1,2,3,4]这个过程就叫离散化。
- 离散化,就是当我们只关心数据的大小关系时,用排名代替原数据进行处理的一种预处理方法 离散化本质上是一种哈希,它在保持原序列大小关系的前提下把其映射成正整数。当原数据很大或含有负数、小数时,难以表示为数组下标,一些算法和数据结构(如BIT)无法运作,这时我们就可以考虑将其离散化。
- 流程

字符串操作中树的思想
class Trie {
private:
bool isEnd;
Trie* next[26];
public:
/** Initialize your data structure here. */
Trie() {
isEnd = false;
memset(next, 0, sizeof(next));
}
/** Inserts a word into the trie. */
void insert(string word) {
Trie* cur = this;
for (auto& c : word) {
if (!cur->next[c-'a'])
cur->next[c-'a'] = new Trie();
cur = cur->next[c-'a'];
}
cur->isEnd = true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
Trie* cur = this;
for (auto& c : word) {
cur = cur->next[c-'a'];
if (!cur) return false;
}
return cur->isEnd;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
Trie* cur = this;
for (auto& c : prefix) {
cur = cur->next[c-'a'];
if (!cur) return false;
}
return true;
}
};
字符编码中树的思想
- Huffman编码:一种不等长编码方式,频率越高,编码越短
- 消除二义性:即前缀码特性,任何一个字符编码不能是另一个字符编码的前缀!
- 思想:贪心思想,每次从树的集合中取出没有双亲 且 权值 最小的 两棵树作为左右子树,左编码为 0,右编码为 1
- 结果:从根节点到叶节点 上 路径组成的 二进制 编码 即为 该字符的 Huffman 编码!
- 代码:TODO

图
图的表示
- 邻接矩阵
- 邻接表
图的连通性
Kosaraju算法
二分图
- L886
- 二分图的判别 染色法
- 二分图的匹配 匈牙利算法
最短路径
Dijkstra算法 不能处理负权
朴素版dijkstra适合稠密图
- 集合S为已经确定最短路径的点集。邻接矩阵
- 初始化距离,一号结点的距离为零,其他结点的距离设为无穷大(看具体的题)。
- 循环n次,每一次将集合S之外距离最短X的点加入到S中去(这里的距离最短指的是距离1号点最近。点X的路径一定最短,基于贪心,严格证明待看)。然后用点X更新X邻接点的距离。
| 寻找路径最短的点: | O(n^2) |
|---|---|
| 加入集合S: | O(n) |
| 更新距离: | O(m) |
| 时间复杂度为 | O(n^2) |
#include 堆优化版dijkstra适合稀疏图
- 邻接表 堆优化版的dijkstra是对朴素版dijkstra进行了优化,在朴素版dijkstra中时间复杂度最高的寻找距离最短的点O(n^2)可以使用最小堆优化。
- 一号点的距离初始化为零,其他点初始化成无穷大。
- 将一号点放入堆中。
- 不断循环,直到堆空。每一次循环中执行的操作为:
- 弹出堆顶(与朴素版diijkstra找到S外距离最短的点相同,并标记该点的最短路径已经确定)。
- 用该点更新临界点的距离,若更新成功就加入到堆中
| 寻找路径最短的点 | O(n) |
|---|---|
| 加入集合S | O(n) |
| 更新距离 | O(mlogn) |
#include >& wei, vector& dist, vector& vis) {
int Dijstra(vector<vector<pii>>& gra, vector<uint>& dist, vector<bool>& vis) {
int n = gra.size(); // 邻接表
// 最小堆 按距离排序 (距离, 节点序号)
priority_queue<pii, vector<pii>, greater<pii>> Q;
Q.push({0, 0}); // (dist, idx)
while (!Q.empty()) {
pii X = Q.top(); Q.pop();
int idx = X.second;
// uint distance = X.first;
if (vis[idx]) continue;
vis[idx] = true;
for (int i = 0; i < gra[idx].size(); i++) {
int new_idx = gra[idx][i].first;
int wei = gra[idx][i].second;
if (dist[new_idx] > dist[idx] + wei) {
dist[new_idx] = dist[idx] + wei;
Q.push({dist[new_idx], new_idx});
}
}
}
if (dist[n-1] == INT_MAX) return -1;
return dist[n-1];
}
int main() {
int n, m;
cin >> n >> m;
// vector> wei(n, vector(n, 100000));
vector<vector<pii>> gra(n);
vector<uint> dist(n, INT_MAX);
vector<bool> vis(n, false);
dist[0] = 0;
for (int i = 0; i < m; i++) {
int p, q, k;
cin >> p >> q >> k;
// wei[p - 1][q - 1] = min(wei[p - 1][q - 1], uint(k));
gra[p - 1].push_back({q - 1, uint(k)});
}
// Dijkstra
// cout << Dijstra(wei, dist, vis) << endl;
cout << Dijstra(gra, dist, vis) << endl;
return 0;
}
最小生成树
- Prime
并查集算法 Union-find
-
图都是通过邻接表或点对表示边而非邻接矩阵存储的,这样能够提高遍历和存储的时间和空间效率。但实际上,这两种方式也有一个严重的缺陷:不方便查询、修改指定的两点u和v的关系。于是在这种情况下的这两种方式构成的图的连通性也非常难以判断。
-
并查集,其实是相互连通的各点通过父节点表示法构成的森林(很多棵树的集合),我们判断两点是否相互连通,实际上就是通过他们是否在同一棵树内。
-
解决图中的【动态连通性问题】
原理
动态连通性其实可以抽象成给一幅图连线。
Union-find的算法框架:
使用树结构来实现,具体用数组形式,保存节点的父子关系!
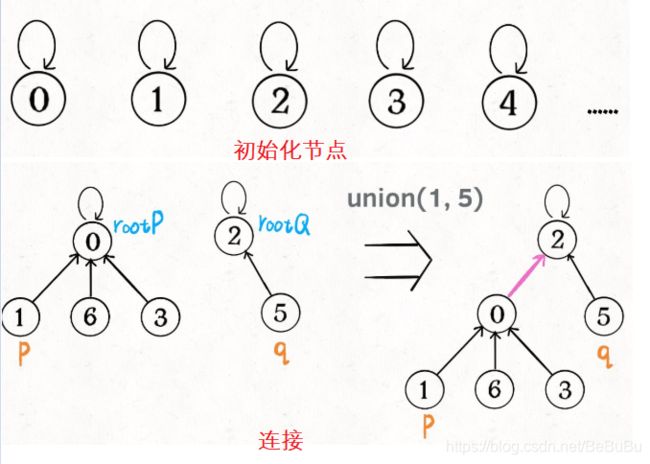
这样,如果节点p和q连通的话,它们一定拥有相同的根节点:
class UF {
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 将两棵树合并为一棵
parent[rootP] = rootQ;
// parent[rootQ] = rootP 也一样
count--; // 两个分量合二为一
}
/* 返回某个节点 x 的根节点 */
private int find(int x) {
// 根节点的 parent[x] == x
while (parent[x] != x)
x = parent[x];
return x;
}
/* 返回当前的连通分量个数 */
public int count() {
return count;
}
/*是否连通 = 是否有公共父节点*/
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
}
上述的实现有两个缺点:1 树结构不平衡,可能会出现头重脚轻的情况;2 不平衡树导致find,union,connected的时间复杂度都是 O(N)
树的平衡性优化 / 启发式(按秩)合并
O(N) ⇒ O(lgN)
我们其实是希望,小一些的树接到大一些的树下面,这样就能避免头重脚轻,更平衡一些。
- 额外使用一个size数组,记录每棵树包含的节点数,我们不妨称为「重量」:
class UF {
private int count;
private int[] parent;
// 新增一个数组记录树的“重量”
private int[] size;
public UF(int n) {
this.count = n;
parent = new int[n];
// 最初每棵树只有一个节点
// 重量应该初始化 1
size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 小树接到大树下面,较平衡
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
}
路径压缩
进一步压缩每棵树的高度,使树高始终保持为常数?
O(lgN) ==> O(1)
private int find(int x) {
while (parent[x] != x) {
// 进行路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
实际中,每次find都会进行路径压缩,所以树本来就不可能增长到这么高,你的这种担心应该是多余的。height <= 3
回滚并查集 / 带撤销并查集
必须要按秩合并来实现, 思路大概是用栈来维护每次修改的位置与修改前的内容; 使用stack
可持久化并查集 TODO
主席树(可持久化线段树)线段树
即 共享儿子
我们将支持回退操作的数据结构称为可持久化数据结构。
应用
class UF {
// 连通分量个数
private int count;
// 存储一棵树
private int[] parent;
// 记录树的“重量”
private int[] size;
public UF(int n) {
this.count = n;
parent = new int[n];
size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
// 小树接到大树下面,较平衡
if (size[rootP] > size[rootQ]) {
parent[rootQ] = rootP;
size[rootP] += size[rootQ];
} else {
parent[rootP] = rootQ;
size[rootQ] += size[rootP];
}
count--;
}
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
private int find(int x) {
while (parent[x] != x) {
// 进行路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
public int count() {
return count;
}
}
既然有了路径压缩,size 数组的重量平衡还需要吗?
注意,有了平衡会好点,如下图情况:
130. 被围绕的区域
填充被围绕的区域,边界区域不会被围绕!
X X X X
X O O X
X X O X
X O X X
运行你的函数后,矩阵变为:
X X X X
X X X X
X X X X
X O X X
W1 DFS
思想:
- 先在矩阵的四条边找‘O’,将其递归赋值为‘$’;
- 最后再for循环赋值,‘O’ - ‘X’; $'- ‘O’
class Solution {
public:
void solve(vector<vector<char>>& board) {
for (int i = 0; i < board.size(); ++i) {
for (int j = 0; j < board[0].size(); ++j) {
if (board[i][j] == 'O' &&
(i == 0 || i == board.size() - 1 ||
j == 0 || j == board[0].size() - 1)) {
helper(board,i,j);
}
}
}
for (int i = 0; i < board.size(); ++i) {
for (int j = 0; j < board[0].size(); ++j) {
if (board[i][j] == 'O') board[i][j] = 'X';
else if (board[i][j] == '$') board[i][j] = 'O';
}
}
}
void helper(vector<vector<char>>& board, int row, int col) {
int h = board.size(), w = board[0].size();
if (row < 0 || row >= h || col < 0 || col >= w) return;
if (board[row][col] == 'X' || board[row][col] == '$') return;
board[row][col] = '$';
helper(board,row-1,col);
helper(board,row+1,col);
helper(board,row,col-1);
helper(board,row,col+1);
}
};
W2 BFS
宽度搜索类似,在矩阵的四边使用队列载入‘O’,标记+push相邻‘O’
后面还是使用双for’循环!
W3 Union-find
思想:
使用图方法,类似CRF一样构造这种表示:
给不能修改的‘O’一个公共根节点dummy!
一些细节:
- 用坐标表示节点,二维数组拉长为一维数组!
class Solution {
private:
class uf { // 并查集 (不可删除节点)
private:
int con;
vector<int> sz;
vector<int> pa;
public:
uf (int n) {
for (int i = 0; i < n; ++i) {
sz.push_back(1);
pa.push_back(i);
}
this->con = n;
}
void merge(int x, int y) { // union
// 按秩合并
int rx = find(x);
int ry = find(y);
if (rx == ry) return;
if (sz[rx] > sz[ry]) {
pa[ry] = rx;
sz[rx] += sz[ry];
} else {
pa[rx] = ry;
sz[ry] += sz[rx];
}
con--;
}
int find(int x) {
// 路径压缩
while (pa[x] != x) {
pa[x] = pa[pa[x]];
x = pa[x];
}
return x;
}
bool connect(int x, int y) {
return find(x) == find(y);
}
int count() {
return con;
}
};
public:
void solve(vector<vector<char>>& board) {
if (board.empty() || board[0].empty()) return;
int h = board.size(), w = board[0].size();
int n = h * w;
uf u(n+1); // 构建并查集 + dummy节点
for (int i = 0; i < h; ++i) {
for (int j = 0; j < w; ++j) {
int m = w*i+j;
if (board[i][j] == 'O' && (i == 0 || j == 0 || i == h - 1 || j == w - 1))
u.merge(m,n); // 边界点
else if (board[i][j] == 'O') { // 和边界相连的'O'点
if (i-1>=0&&board[i-1][j]=='O') u.merge(m,m-w);
if (i+1<h&&board[i+1][j]=='O') u.merge(m,m+w);
if (j-1>=0&&board[i][j-1]=='O') u.merge(m,m-1);
if (j+1<w&&board[i][j+1]=='O') u.merge(m,m+1);
}
}
}
for (int i = 0; i < h; ++i) {
for (int j = 0; j < w; ++j) {
int m = i*w+j;
if (board[i][j] == 'O' && !u.connect(m,n))
board[i][j] = 'X';
}
}
}
};
990. 等式方程的可满足性
输入: [ " a = = b " , " b ! = c " , " c = = a " ] ["a==b","b!=c","c==a"] ["a==b","b!=c","c==a"]
输出: f a l s e false false
- 将 equations 中的算式根据 = = == == 和 ! = != != 分成两部分,先处理 = = == == 算式,使得他们通过相等关系各自勾结成门派;
- 然后处理 ! = != != 算式,检查不等关系是否破坏了相等关系的连通性。
class Solution {
private:
class uf { // 并查集 (不可删除节点)
...
};
public:
bool equationsPossible(vector<string>& equations) {
vector<int> e, ne;
uf u(26);
for (int i = 0; i < equations.size(); ++i) {
if (equations[i][1] == '=') e.push_back(i);
else ne.push_back(i);
}
for (int i = 0; i < e.size(); ++i)
u.merge(equations[e[i]][0]-'a', equations[e[i]][3]-'a');
for (int i = 0; i < ne.size(); ++i) {
if (u.connect(equations[ne[i]][0]-'a', equations[ne[i]][3]-'a'))
return false;
}
return true;
}
};
拓扑排序
- 针对有向图
- 对图节点进行排序 成一维数组
- A -> B,A出现在B的前面
- 如果且仅当图形没有定向循环,即如果它是有向无环图(DAG),则拓扑排序是可能的
- 以课程表为例子:[[1, 0], [0, 2], [1, 3]],表示0课程完成之后,1课程才能修,输出一种修课的顺序
class Solution {
public:
bool topSort(vector<vector<int>>& G, vector<int>& O, vector<int>& D) {
int N = D.size(), idx = 0;
queue<int> Q; // 入度为0才能做学习起点
for (int i = 0; i < N; i++)
if (D[i] == 0) Q.push(i);
while (!Q.empty()) {
int X = Q.front(); Q.pop();
O[idx++] = X;
for (int i = 0; i < G[X].size(); i++) {
int x = G[X][i]; D[x]--;
if (D[x] == 0) Q.push(x);
}
G[X].clear();
}
if (idx == N) return true;
return false;
}
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<int> inD(numCourses), res(numCourses); // 入度表 课程排序
vector<vector<int>> G(numCourses); // 邻接表
for (int i = 0; i < prerequisites.size(); i++) {
G[prerequisites[i][1]].push_back(prerequisites[i][0]);
inD[prerequisites[i][0]]++;
}
if (topSort(G, res, inD)) return res;
return {};
}
};