RL 实践(0)—— 及第平台辛丑年冬赛季【Rule-based policy】
- 本学期选了一个数据科学相关的实验课,大作业是复现一个数据挖掘相关竞赛的冠军算法,为了实践一下 RL,我找了半天之后专门选了一个比较简单的 RL 竞赛
- 但是开始弄了才发现,这个竞赛的冠军方法竟然是一个纯规则方法,这下尴尬了,不但没实践成,还复现得很痛苦。总之先把报告发上来水一篇博文吧,用这个 Rule-based 方法作为 RL 实践系列的第一篇
- 引用信息
- 赛题链接:RLChina 智能体挑战赛 - 辛丑年冬赛季
- 冠军原始代码:Luanshaotong / Competition_Olympics-Running
- 我的复现代码:[JiDi_platform] competition-olympics-running (Rule-based) (注:后文中关于 “代码结构/代码内容/注释“ 等内容的说明均基于此仓库)
- 我的 presentation slide:slide
- 【RLChina 智能体挑战赛】辛丑年冬赛季赛题讲解
- 【RLChina 智能体挑战赛】及第辛丑年冬赛季线上算法分享会
文章目录
- 0. 背景说明
-
- 0.1 赛题介绍
-
- 0.1.1 规则
- 0.1.2 赛题特点和挑战
- 0.2 关于本报告的说明
- 1. Learning Based 方法
-
- 1.0 强化学习背景
-
- 1.0.1 基础概念
- 1.0.2 算法分类
- 1.1 算法模型
-
- 1.1.1 模型选择
- 1.1.2 调参技巧 & 超参数设置
- 1.2 各队伍使用的 tricks (for RL)
-
- 1.2.1 第五名队伍
- 1.2.2 第四名队伍
- 1.2.3 第三名队伍
- 1.3 小结
- 2. Rule based 方法
-
- 2.1 规则设计(特征工程)
-
- 2.1.1 分析
- 2.1.2 冠军方案思路
- 2.2 规则构造细节(特征构造方法)
-
- 2.2.1 基础设定
- 2.2.2 包装原始观测
- 2.2.3 识别箭头
- 2.2.4 找出所有可行边和目标边
- 2.2.5 生成动作
- 2.2.6 转向角度补偿(提前转向)
- 2.2.7 其他
- 2.3 实验评估
-
- 2.3.1 复现冠军方案
- 2.3.2 性能评估
- 3. 分析和改进
-
- 3.1 方案分析
- 3.2 改进展望
- 4.总结
0. 背景说明
0.1 赛题介绍
0.1.1 规则
-
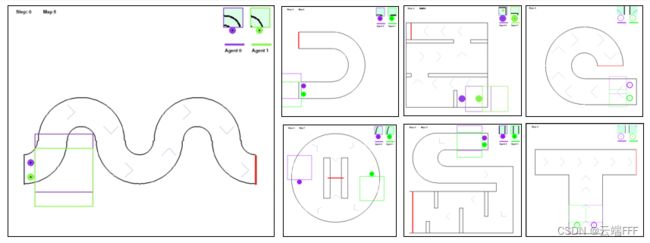
本实验选择的比赛为 2021/11/22 - 2022/1/20 进行的 “RLChina 智能体挑战赛 - 辛丑年冬赛季”,该竞赛由 RLChina 联合及第平台共同举办,使用及第平台的 “奥林匹克 跑步运动” 作为比赛科目
-
- 对战双方各控制一个有相同质量和半径的弹性小球智能体,最先触及终点线的一方获胜
- 测评时地图随机,并且可能出现训练时没见过的地图(总共11张地图)
- 智能体可以互相碰撞,也可以碰撞墙壁,但会损失一定的速度
- 智能体自身有能量,每步消耗的能量与施加的驱动力和位移成正比
- 智能体能量以固定速率恢复,如果能量衰减到零,则不能加力
- 智能体的观测为自身朝向前方25*25的矩形区域,观测值包括墙壁、终点线、对手和跑道方向辅助箭头
- 当有一个智能体到达终点(红线)或环境达到最大步数500步时环境结束,先冲过终点的一方获胜,若双方均未过线则平局
-
总结一下关键信息
0.1.2 赛题特点和挑战
-
本题有如下特点
-
部分可观测:agent 只能感知局部信息,全局信息丢失,这会给状态空间的设计带来很大的困难。下面两个 agent 全局位置不同,但是观测是相同的,agent 就无法区分这两个状态

-
泛化性挑战:测试时会出现未见地图,这是本题的最大难点,因为 RL 算法本身不具备这样的泛化性设计
Note: RL 考虑的泛化性是在同一张地图的任意位置出发都能完成任务
局部观测赋予 agent 一定的地图泛化能力,如果直接用原始观测或从中提取特征作为状态,则 agent 学到的是从这个 25*25 的观测特征分布到动作的映射,在所有地图的生成满足某个生成规则,训练地图中包含所有地图构成要素,且有一定多样性的前提下,可能可以进行一定的泛化。坏消息是,各个地图间区别很大
- 有些地图有箭头提示,有些没有
- 有些地图有十字路口,有些没有
- 有些地图中间有墙壁阻挡,有些没有
各个地图中包含的元素太多且差异很大,再加上部分观测导致的信息丢失,这个 25*25 观测的特征空间变得更大,相比而言训练地图数量就显得太少,这样直接学出的观测特征分布到动作的映射很容易过拟合,因此最好能考虑联合历史交互数据考虑构造新状态特征(比如用 RNN)。另外,状态和奖励中没有和能量有关的表征,在训练地图上通过强化学出来的分配策略往往过于激进,几乎无法泛化,可以考虑硬编码能量分配规则
-
稀疏奖励:原始环境中仅在取胜或平局达到终点时可以得到 1 的奖励,非常稀疏,需要考虑根据观测信息构造内部奖励
-
环境本身是确定性转移,随机性来自和对手交互,这个对抗其实不是很强,超过或落后对手一定距离即可看作没有对手存在
-
由于起点位置固定,使用前几帧就能判断是那一张训练训练地图!这样有可能硬编码一些动作
-
-
总结一下:部分观测 + 地图间差异大 = 极端的 POMDP 问题 = 信息缺失严重,特征工程难做
- 直接用神经网络提取原始观测特征,效果不佳(针对 POMDP 问题,通常使用 RNN 融合历史数据来提取状态特征)
- 地图数量太少不好提取地图分布,没法用 Meta RL
- 联合训练会导致观测特征空间变得非常大,性能相比各个地图单独训练时反而下降很多(既然能区分出当前的地图,可以考虑各地图单独训练)
- 能量分配策略几乎不可能泛化到新地图
Note: 关键是 agent 位置、速度、能量等重要信息缺失
0.2 关于本报告的说明
-
Note:由于本实验选题为强化学习,而冠军方法是一个纯规则方法(不涉及任何机器学习内容),这和《数据科学与应用实验课概述》ppt 中假定的监督学习类竞赛有很大不同,所以本报告不会完全按照上述 PPT 所规定之格式撰写
-
先看一下比赛结果
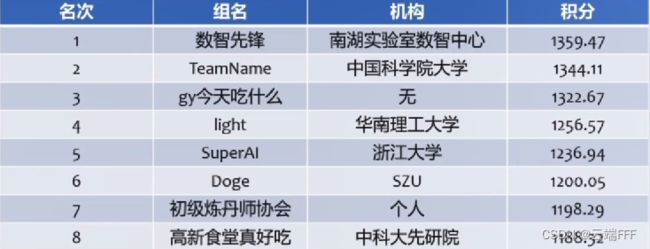
前五名中,第一第二都是纯规则方法,而三到五名都是机器学习方法,他们使用的方法 + tricks 概括如下- 第一名(得分 1359.47):【规则智能体】实时构建地图并规划路线
- 第二名(得分 1344.11):【规则智能体】实时检测箭头和墙壁位置导航
- 第三名(得分 1322.67):【强化学习】PPO + 全连接网络提取特征 + reward shaping + self-play + 额外规则
- 第四名(得分 1256.57):【模仿学习】人工示范 + 监督学习(行为克隆)
- 第五名(得分 1236.94):【强化学习】PPO + 状态叠帧CNN提取特征 + 动作空间离散化 + self-play
注意到一共出现了三类方法,模仿学习和强化学习都可以算到机器学习的范畴,而前两名的规则类方法硬要说的话仅仅就是做了一个很复杂的数据预处理而已
-
一个强化学习比赛却被规则类 agent 夺魁,这是值得思考的一件事,从学术的角度看,这体现了强化学习方法的泛化性问题
-
考虑到本课程性质,本报告会综合分析前五名的方法,这样不但能包含一些机器学习的相关内容,还可以针对序列决策任务,对 learning-based 和 rule-based 方法的性质做一些比较
1. Learning Based 方法
1.0 强化学习背景
- 为了便于 1.1.1 节中分析 PPO 算法优势及其推导,先介绍必要的基础概念
1.0.1 基础概念
- 强化学习是在与环境的交互中收集数据,通过最大化累计折扣奖励来学习最优策略的一种方法,适用于解决序列决策问题。RL 交互示意图如下

- 通常将以上交互建模为马尔可夫决策过程 MDP < S , A , R , P , γ , ( D ) > <\mathcal{S,A},R,P,\gamma,(\mathcal{D})> <S,A,R,P,γ,(D)>,交互行为产生一系列 “状态、动作、奖励” 序列,称之为 episode,形如
s 0 , a 0 , r 1 , s 1 , a 1 , r 2 , . . . s_0,a_0,r_1,s_1,a_1,r_2,... s0,a0,r1,s1,a1,r2,...其中奖励信号 R t + 1 = R ( S t , A t ) R_{t+1} = R(S_t,A_t) Rt+1=R(St,At) 是 agent 可以获取的指导其行为的唯一信号,注意该信号是和 ( s , a ) (s,a) (s,a) pair 绑定的,为了解决 RL 的 Credit Assignment Problem,我们设计出一套收益和价值函数机制,具体而言,把某个 episode 上从 t t t 时刻开始的收益/回报 (return ) 定义为
G t = ⋅ R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . = ∑ k = 0 ∞ γ k R t + k + 1 G_t \stackrel{·}{=} R_{t+1} + \gamma R_{t+2} +\gamma^2R_{t+3}+... = \sum_{k=0}^\infin \gamma^kR_{t+k+1} Gt=⋅Rt+1+γRt+2+γ2Rt+3+...=k=0∑∞γkRt+k+1这可以被看作该条 episode 上 “进入状态 S t S_t St ” 或 “在状态 S t S_t St 执行动作 A t A_t At” 的收益,求它关于 agent 策略 π \pi π 的条件期望,即可评价某个 s s s 或 ( s , a ) (s,a) (s,a) 的好坏,这就是价值函数
v π ( s ) = ⋅ E π [ G t ∣ S t = s ] q π ( s , a ) = ⋅ E π [ G t ∣ S t = s , A t = a ] \begin{aligned} &v_\pi(s) \stackrel{·}{=} \mathbb{E}_\pi[G_t|S_t = s]\\ &q_\pi(s,a) \stackrel{·}{=} \mathbb{E}_\pi[G_t|S_t = s,A_t=a] \end{aligned} vπ(s)=⋅Eπ[Gt∣St=s]qπ(s,a)=⋅Eπ[Gt∣St=s,At=a]注意到 G t G_t Gt 定义中存在递归关系,由此可以推出任意策略 π \pi π 或最优策略 π ∗ \pi^* π∗ 下相邻 s s s 或 ( s , a ) (s,a) (s,a) 之间价值的迭代关系(以 V V V 函数为例如下)
v π ( s ) = E π [ R t + 1 + γ G t + 1 ∣ S t = s ] = ∑ a π ( a ∣ s ) ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) [ r + γ E π [ G t + 1 ∣ S t + 1 = s ′ ] ] = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] v ∗ ( s ) = max a ∈ A ( s ) q π ∗ ( s , a ) = max a E π ∗ [ G t ∣ S t = s , A t = a ] = max a E π ∗ [ R t + 1 + γ G t + 1 ∣ S t = s , A t = a ] = max a E [ R t + 1 + γ v ∗ ( S t + 1 ) ∣ S t = s , A t = a ] = max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v ∗ ( s ′ ) ] \begin{aligned} &\begin{aligned} v_{\pi}(s) &= \mathbb{E}_{\pi}[R_{t+1} + \gamma G_{t+1}| S_t=s] \\ &= \sum_a\pi(a|s)\sum_{s'}\sum_r p(s',r|s,a)[r+\gamma\mathbb{E}_\pi[G_{t+1}|S_{t+1}=s']]\\ &= \sum_a\pi(a|s)\sum_{s',r} p(s',r|s,a)[r+\gamma v_\pi(s')]\\ \end{aligned}\\ &\begin{aligned} v_*(s) &= \max_{a\in\mathcal{A(s)}}q_{\pi_*}(s,a) \\ &= \max_a \mathbb{E}_{\pi_*}[G_t|S_t=s,A_t=a] \\ &= \max_a \mathbb{E}_{\pi_*}[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a] \\ &= \max_a \mathbb{E}[R_{t+1}+\gamma v_*(S_{t+1})|S_t=s,A_t=a] \\ &= \max_a \sum_{s',r}p(s',r|s,a)[r+\gamma v_*(s')] \end{aligned} \end{aligned} vπ(s)=Eπ[Rt+1+γGt+1∣St=s]=a∑π(a∣s)s′∑r∑p(s′,r∣s,a)[r+γEπ[Gt+1∣St+1=s′]]=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)]v∗(s)=a∈A(s)maxqπ∗(s,a)=amaxEπ∗[Gt∣St=s,At=a]=amaxEπ∗[Rt+1+γGt+1∣St=s,At=a]=amaxE[Rt+1+γv∗(St+1)∣St=s,At=a]=amaxs′,r∑p(s′,r∣s,a)[r+γv∗(s′)]这就是 Bellman equation 和 Bellman optimal equation,利用这两个公式,就能把和某个具体 ( s , a ) (s,a) (s,a) pair 绑定的奖励信号沿着 episode 反向传播,使得指导信号在动作状态空间中不断传播,直到最后价值收敛,解决任意策略 π \pi π 的 Credit Assignment Problem
1.0.2 算法分类
- 按照算法学习的内容,大体上可以把 RL 算法分成三类
- Value-based 方法:这类方法基于 value iteration 思想,直接利用 Bellman optimal equation 学习出最优动作价值函数 Q ∗ Q^* Q∗,进而导出最优策略 π ∗ \pi^* π∗
- Policy Gradient 方法:这类方法基于 policy iteration 思想,交替执行 “利用 Bellman equation 评估当前策略” 和 “优化策略” 两步,直接学习能够最大化期望 return 的最优策略 π ∗ \pi^* π∗,具体实现时常将其表示为一个优化问题并用 Gradient-based 优化方法求解。注意 agent 能够获取的唯一指导信号就是 reward 信号,因此优化目标不可能脱离对价值的估计,通常为以下形式
arg max π J ( θ ) = arg max π E S [ V ( S ) ] = arg max π E S , A [ Q ( S , A ) ] \begin{aligned} \arg\max_\pi J(\theta) &= \arg\max_\pi \mathbb{E}_{\mathcal{S}}[V(S)]\\ &= \arg\max_\pi \mathbb{E}_{\mathcal{S,A}}[Q(S,A)]\\ \end{aligned} argπmaxJ(θ)=argπmaxES[V(S)]=argπmaxES,A[Q(S,A)]根据优化过程中是否需要学习完整的价值函数,可以进一步将 Policy Gradient 方法分为以下两类- Policy based 方法:这类方法直接学习策略,其中可能有价值信息作为优化目标的一部分,但不必学习完整的价值函数
- Actor-Critic 方法:这类方法同时学习价值函数和策略,并在每轮迭代中直接使用学到的价值函数输出作为策略网络的优化目标
- 上述讨论可以用示意图如下表示

1.1 算法模型
1.1.1 模型选择
-
注意到使用强化学习的第三名和第五名在模型选择问题上都不约而同地选择了 PPO 算法,故本节讨论 PPO 算法的优势。先看一下各类方法存在的问题
- Value based 类方法的思路基本都是输入一个状态,输出执行各个动作的概率分布,这就要求可行动作必须是可列的,也就是说 Value based 方法仅适用于离散动作空间,该赛题是一个连续控制任务,所以这一类方法都直接排除了
- Policy gradient 类方法可以实现连续控制,通常将策略参数化为策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ)。就像这类方法的名字那样,几乎所有 policy gradient 算法都使用梯度方法对 θ \theta θ 进行优化,假设 g g g 是某轮迭代中计算的梯度或随机梯度值, θ \theta θ 会如下更新
θ ← θ + α g \theta \leftarrow \theta + \alpha g θ←θ+αg其中 α \alpha α 是学习率。这看起来很好,但问题在于强化学习对于策略是非常敏感的, π \pi π 的一点点变化,都可能导致巨大的性能差异,上面这种更新方式可以通过调整 α \alpha α 很好地控制参数 θ \theta θ 的变化,但无法准确且线性地控制经过神经网络后得到的策略 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 的变化,所以梯度优化时很容易 overstep,学到的策略 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 在 sweet point 附近反复震荡,收敛缓慢,样本效率低下
-
解决 Policy gradient 方法问题的一个思路是直接换一种优化方法,以回避上面的更新过程,比如改用置信域优化方法
- 置信域优化是一种经典优化方法,其出发点是:如果对目标函数 J ( θ ) J(\theta) J(θ) 进行优化过于困难,不妨在 θ \theta θ 的当前值 θ n o w \theta_{now} θnow 附近构造一个局部范围内和 J ( θ ) J(\theta) J(θ) 十分相似的替代函数 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow),通过在这个局部范围内最优化 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow) 来更新一次 θ \theta θ 值,反复迭代上述过程直到收敛。注意到这里的置信域半径控制着每一轮迭代中 θ \theta θ 变化的上限,我们通常会让这个半径随优化过程不断减小来避免 overstep,其一步更新和优化过程示意图如下

- 注意到每一轮迭代中,我们都在构造并求解一个小的约束优化问题,这样就不要做 θ ← θ + α g \theta \leftarrow \theta + \alpha g θ←θ+αg 形式的更新了,更重要的是,我们可以更自由地设计置信域约束条件,从而对每轮迭代中 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 的变化进行直接控制
- 置信域优化是一种经典优化方法,其出发点是:如果对目标函数 J ( θ ) J(\theta) J(θ) 进行优化过于困难,不妨在 θ \theta θ 的当前值 θ n o w \theta_{now} θnow 附近构造一个局部范围内和 J ( θ ) J(\theta) J(θ) 十分相似的替代函数 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow),通过在这个局部范围内最优化 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow) 来更新一次 θ \theta θ 值,反复迭代上述过程直到收敛。注意到这里的置信域半径控制着每一轮迭代中 θ \theta θ 变化的上限,我们通常会让这个半径随优化过程不断减小来避免 overstep,其一步更新和优化过程示意图如下
-
把置信域优化方法和 policy based 方法相结合就得到了 TRPO 方法,下面做一些公式推导。记住我们的优化目标是最大化 J ( θ ) = E S [ V π ( a ∣ s ; θ ) ( S ) ] J(\theta) = \mathbb{E}_S[V_{\pi(a|s;\theta)}(S)] J(θ)=ES[Vπ(a∣s;θ)(S)],为了构造 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow),把 θ n o w \theta_{now} θnow 引入 V π ( s ) V_\pi(s) Vπ(s) 中
V π ( s ) = ∑ a π ( a ∣ s ; θ ) ⋅ Q π ( s , a ) = ∑ a π ( a ∣ s ; θ n o w ) ⋅ π ( a ∣ s ; θ ) π ( a ∣ s ; θ n o w ) ⋅ Q π ( s , a ) = E A ∼ π ( a ∣ s ; θ n o w ) [ π ( a ∣ s ; θ ) π ( a ∣ s ; θ n o w ) ⋅ Q π ( s , a ) ] \begin{aligned} V_\pi(s) &= \sum_a \pi(a|s;\theta)·Q_\pi(s,a) \\ &= \sum_a \pi(a|s;\theta_{now})·\frac{\pi(a|s;\theta)}{\pi(a|s;\theta_{now})}·Q_\pi(s,a) \\ &= \mathbb{E}_{A\sim \pi(a|s;\theta_{now})} \big[\frac{\pi(a|s;\theta)}{\pi(a|s;\theta_{now})}·Q_\pi(s,a) \big] \end{aligned} Vπ(s)=a∑π(a∣s;θ)⋅Qπ(s,a)=a∑π(a∣s;θnow)⋅π(a∣s;θnow)π(a∣s;θ)⋅Qπ(s,a)=EA∼π(a∣s;θnow)[π(a∣s;θnow)π(a∣s;θ)⋅Qπ(s,a)]这样优化目标就变成
J ( θ ) = E S [ V π ( a ∣ s ; θ ) ( S ) ] = E S [ E A [ π ( a ∣ s ; θ ) π ( a ∣ s ; θ n o w ) ⋅ Q π ( s , a ) ] ] = E S , A [ π ( a ∣ s ; θ ) π ( a ∣ s ; θ n o w ) ⋅ Q π ( s , a ) ] \begin{aligned} J(\theta) &= \mathbb{E}_S[V_{\pi(a|s;\theta)}(S)] \\ &= \mathbb{E}_S\big[\mathbb{E}_A \big[\frac{\pi(a|s;\theta)}{\pi(a|s;\theta_{now})}·Q_\pi(s,a) \big]\big] \\ &= \mathbb{E}_{S,A} \big[\frac{\pi(a|s;\theta)}{\pi(a|s;\theta_{now})}·Q_\pi(s,a) \big] \end{aligned} J(θ)=ES[Vπ(a∣s;θ)(S)]=ES[EA[π(a∣s;θnow)π(a∣s;θ)⋅Qπ(s,a)]]=ES,A[π(a∣s;θnow)π(a∣s;θ)⋅Qπ(s,a)]
注意到这个原始优化目标中有两个不好处理的点- 要对动作空间 A \mathcal{A} A 和状态空间 S \mathcal{S} S 做积分,这个积分没法做。我们利用 MC 的思想构造替代优化目标,先用 π ( a ∣ s ; θ n o w ) \pi(a|s;\theta_{now}) π(a∣s;θnow) 交互得到一批具体的 transition 数据,再用它们 π ( a ∣ s ; θ ) π ( a ∣ s ; θ n o w ) ⋅ Q π ( s , a ) \frac{\pi(a|s;\theta)}{\pi(a|s;\theta_{now})}·Q_\pi(s,a) π(a∣s;θnow)π(a∣s;θ)⋅Qπ(s,a) 的均值代替期望
- 要估计优化得到的 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 下的 Q Q Q 价值。我们认为置信域内 Q π ( a ∣ s ; θ n o w ) Q_{\pi(a|s;\theta_{now})} Qπ(a∣s;θnow) 是 Q π ( a ∣ s ; θ ) Q_{\pi(a|s;\theta)} Qπ(a∣s;θ) 的近似,而每个 ( s , a ) (s,a) (s,a) 在其轨迹中的具体 return g g g 又是 Q π ( a ∣ s ; θ n o w ) Q_{\pi(a|s;\theta_{now})} Qπ(a∣s;θnow) 的近似,这样就可以用 g g g 估计 Q π ( a ∣ s ; θ ) ( s , a ) Q_{\pi(a|s;\theta)}(s,a) Qπ(a∣s;θ)(s,a)
解决两个问题后构造出的替代目标函数 L ( θ ∣ θ n o w ) L(\theta|\theta_{now}) L(θ∣θnow) 如下:
L ( θ ∣ θ n o w ) = 1 n ∑ i = 1 n π ( a i ∣ s i ; θ ) π ( a i ∣ s i ; θ n o w ) ⋅ g i L(\theta|\theta_{now}) = \frac{1}{n}\sum_{i=1}^n \frac{\pi(a_i|s_i;\theta)}{\pi(a_i|s_i;\theta_{now})}·g_i L(θ∣θnow)=n1i=1∑nπ(ai∣si;θnow)π(ai∣si;θ)⋅gi再加上置信域约束,每轮迭代中构造出的约束优化问题为
θ n e w ← arg max θ L ( θ ∣ θ n o w ) s.t. θ ∈ N ( θ n o w ) \theta_{new} \leftarrow \arg\max_\theta L(\theta|\theta_{now}) \space\space\space\space\space\space\space \text{s.t.} \space\space\theta \in \mathcal{N}(\theta_{now}) θnew←argθmaxL(θ∣θnow) s.t. θ∈N(θnow)为了避免策略的 overstep 问题,直接把更新前后的策略差异的约束作为 θ \theta θ 的约束条件,即
θ ∈ N ( θ n o w ) ⇒ 1 n ∑ i = 1 n KL [ π ( a ∣ s ; θ n o w ∣ ∣ π ( a ∣ s ; θ ) ) ] < △ \theta \in \mathcal{N}(\theta_{now}) \space\space\space \Rightarrow\space\space \frac{1}{n}\sum_{i=1}^n \text{KL}\big[\pi(a|s;\theta_{now} || \pi(a|s;\theta)) \big] < \triangle θ∈N(θnow) ⇒ n1i=1∑nKL[π(a∣s;θnow∣∣π(a∣s;θ))]<△持续迭代求解上述约束优化问题直至策略收敛的方法就是 TRPO,注意我们不再需要手动设置梯度更新步长 α \alpha α 了,且能有效控制每轮迭代中策略的变化程度,这就很好地解决了策略网络优化时的 overstep 问题,另外 TRPO 对超参数(如置信域半径)也不敏感,即使超参设置较差,性能也不会下降很多。但是,TRPO 也引入了新问题:上面这个约束优化问题求解起来非常困难,编程实现也很繁琐 -
PPO 巧妙地将 TRPO 中的约束优化问题转换为了一个无约束优化问题,其优化目标如下
J P P O θ k ( θ ) ≈ ∑ ( s t , a t ) min ( π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ k ) A θ k ( s t , a t ) , clip ( π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ k ) , 1 − ε , 1 + ε ) A θ k ( s t , a t ) ) \begin{aligned} J_{P P O}^{\theta^{k}}(\theta) \approx \sum_{\left(s_{t}, a_{t}\right)} \min &\left(\frac{\pi\left(a_{t} | s_{t};\theta\right)}{\pi\left(a_{t} | s_{t};{\theta^{k}}\right)} A^{\theta^{k}}\left(s_{t}, a_{t}\right)\right.,\\ &\left.\operatorname{clip}\left(\frac{\pi\left(a_{t} | s_{t};\theta\right)}{\pi\left(a_{t} | s_{t};{\theta^{k}}\right)}, 1-\varepsilon, 1+\varepsilon\right) A^{\theta^{k}}\left(s_{t}, a_{t}\right)\right) \end{aligned} JPPOθk(θ)≈(st,at)∑min(π(at∣st;θk)π(at∣st;θ)Aθk(st,at),clip(π(at∣st;θk)π(at∣st;θ),1−ε,1+ε)Aθk(st,at))其中主要有两点比较重要-
引入了优势函数 A θ k ( s t , a t ) = Q π ( a ∣ s ; θ k ) ( s t , a t ) − V π ( a ∣ s ; θ k ) ( s t ) A^{\theta^{k}}\left(s_{t}, a_{t}\right) = Q_{\pi(a|s;\theta^k)}(s_t,a_t) - V_{\pi(a|s;\theta^k)}(s_t) Aθk(st,at)=Qπ(a∣s;θk)(st,at)−Vπ(a∣s;θk)(st) ,优势函数代表在状态 s t s_t st 处执行动作 a t a_t at 带来了多大的好处,其关键性质是
E a ∼ π θ [ A π θ ( s , a ) ] = E a ∼ π θ [ Q π θ ( s , a ) ] Var ( A π θ ( s , a ) ) < Var ( Q π θ ( s , a ) \mathbb{E}_{a\sim{\pi^\theta}}[A_{\pi^\theta}(s,a)] = \mathbb{E}_{a\sim{\pi^\theta}}[Q_{\pi^\theta}(s,a)] \\ \text{Var}(A_{\pi^\theta}(s,a)) < \text{Var}(Q_{\pi^\theta}(s,a) Ea∼πθ[Aπθ(s,a)]=Ea∼πθ[Qπθ(s,a)]Var(Aπθ(s,a))<Var(Qπθ(s,a) 优势函数 A A A 相比状态动作价值函数 Q Q Q 具有相同的期望和更小的方差,在 policy gradient 类方法中涉及到 Q Q Q 函数的地方几乎都可以直接替换为 A A A 函数,这是一个常用 trick -
特殊设计的目标函数,这个乍看起来比较复杂,但其实上就是在给优势函数 A θ k A^{\theta^{k}} Aθk 选择一个系数 min ( π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ k ) , clip ( π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ k ) , 1 − ε , 1 + ε ) ) \min \left(\frac{\pi\left(a_{t} | s_{t};\theta\right)}{\pi\left(a_{t} | s_{t};{\theta^{k}}\right)}, \operatorname{clip}\big(\frac{\pi\left(a_{t} | s_{t};\theta\right)}{\pi\left(a_{t} | s_{t};{\theta^{k}}\right)}, 1-\varepsilon, 1+\varepsilon\big)\right) min(π(at∣st;θk)π(at∣st;θ),clip(π(at∣st;θk)π(at∣st;θ),1−ε,1+ε)),其中后者就是把前者裁剪到 [ 1 − ϵ , 1 + ϵ ] [1-\epsilon,1+\epsilon] [1−ϵ,1+ϵ] 而已,直接将两个系数的曲线如下画出来
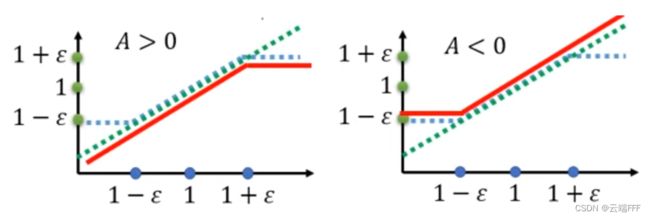
其中蓝色绿色虚线是 π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ k ) \frac{\pi\left(a_{t} | s_{t};\theta\right)}{\pi\left(a_{t} | s_{t};{\theta^{k}}\right)} π(at∣st;θk)π(at∣st;θ),蓝色虚线是 clip ( π ( a t ∣ s t ; θ ) π ( a t ∣ s t ; θ k ) , 1 − ε , 1 + ε ) \operatorname{clip}\big(\frac{\pi\left(a_{t} | s_{t};\theta\right)}{\pi\left(a_{t} | s_{t};{\theta^{k}}\right)}, 1-\varepsilon, 1+\varepsilon\big) clip(π(at∣st;θk)π(at∣st;θ),1−ε,1+ε),红色实线是优势函数 A ( s t , a t ) A(s_t,a_t) A(st,at) 不同取值时 min \min min 操作选出的系数。以左图为例分析, A ( s t , a t ) > 0 A(s_t,a_t)>0 A(st,at)>0 意味着状态 s t s_t st 处动作 a t a_t at 带来了好处,所以为了鼓励 a t a_t at 出现系数应尽量大,但是不要超过 1 + ϵ 1+\epsilon 1+ϵ (就是说 s t s_t st 处选择 a t a_t at 的概率不要比现在高超过 1 + ϵ 1+\epsilon 1+ϵ 倍 ),以免策略网络出现 overstep,而系数小于 1 时说明网络还处于欠拟合状态,没有训练好,这时就不用限制了;右图显示的 A ( s t , a t ) < 0 A(s_t,a_t)<0 A(st,at)<0 情况也同理
可见,PPO 巧妙地将 TRPO 的约束变形成一个 clip \text{clip} clip 加一个 min \min min 操作,不但消除了约束条件,甚至连 KL \text{KL} KL 散度都不用算了,PPO 在保留 TRPO 训练稳定,调参简单的基础上,进一步简化了算法实现
-
-
顺带一提,在 PPO 的原始论文中使用了两个 trick,这两个都是 “插件” 形式的 trick,可以和各种 RL 方法组合
- 使用 GAE 方法,根据经验轨迹 episode 生成优势函数估计值,然后让Critic去拟合这个值,这样不需要太多轨迹即可描述当前策略
- 在优化目标 J J J 中增加策略熵正则项,在优化策略的同时提高策略的熵,这样可以避免训练后期得到的策略过于片面,更好地平衡探索和利用
-
总的来看,PPO 几乎是目前解连续控制问题的主流 model-free DRL 方法中训练最稳定,调参最简单的
- Note:就好像做 CV 时我们首先考虑 CNN 一样,PPO/TD3/SAC 是现在解连续控制强化学习问题的首选方法,它们都是 Policy Gradient 方法,其中
- TD3:在 DPG 的基础上增加了很多 trick 来缓解价值高估问题。其问题在于超参数很多,调参困难,相比而言 PPO 没有那么多参数
- SAC:在策略网络的训练目标中增加策略熵项,从而更好地平衡探索和利用。其问题在于非常依赖 Reward Function,相比而言 PPO 即使用较差的 Reward function 也能训练,而且 PPO 的网络结构要简单一点(不过事实上 SAC 是目前 SOTA 的 model-free 方法)
- 相比而言,PPO 在 “性能” 和 “实现难度 (编程/调参/奖励函数设计)” 间取得了最好的平衡,考虑到比赛时间的紧迫性,PPO 成为大部分走 RL 路线队伍的首选也是意料之中的
1.1.2 调参技巧 & 超参数设置
- 就像前文分析的那样,PPO 对于超参数和奖励函数设计都很鲁棒,通常用默认的超参数即可得到较好的效果(注:RLChina 提供了一个 PPO Demo)
- 因为冠军方法并非 RL 方法,我没有实现 PPO,所以对于调参这块也没有什么体会,不过此处有一篇很好的文章可供参考:深度强化学习调参技巧:以D3QN、TD3、PPO、SAC算法为例,本文作者开发的 ElegantRL 是一个极好的 RL 库,水平在线
1.2 各队伍使用的 tricks (for RL)
1.2.1 第五名队伍
- 使用的 tricks:
- 状态叠帧CNN:在使用 CNN 提取观测信息时,使用连续 4 帧 25*25 的原始图像堆叠作为输入,即输入shape 扩展为 [4,25,25],这样相邻帧之间变化减少,消除抖动,智能体动作更稳定(这个 trick 来自 DQN 论文)
- 连续动作空间离散化:力矩和转向角度都离散化为 11 个点,一共 121 个离散动作,实验发现连续动作空间前期收敛速度快
- Self-play:这是处理多智能体对抗任务的常用 trick,基本思想是和过去的策略网络进行对抗,从而提高自身性能,没有公认的 general schedule 设置,视具体任务而定。该队先把对手选择成随机策略,用 PPO 训练直到胜率稳定在 1,reward 曲线不增长后,进行 self-play(约 1000-2000 轮)
- 80% 时间选择最新的 actor,20% 采样一个旧 actor 模型。每个模型有个 quality score q i ( i = 1 , 2 , . . . , N ) q_i(i=1,2,...,N) qi(i=1,2,...,N),根据 softmax 分布采样。若 self-play 胜率 w i n r winr winr 超过 0.5,模型要扣分以减少其采样概率: q i ← q i − 0.01 N p i ( w i n r − 0.5 ) q_i \leftarrow q_i -\frac{0.01}{N p_i}(winr-0.5) qi←qi−Npi0.01(winr−0.5),其中 p i p_i pi 是第 i i i 个模型被采样概率
- 假设历史模型是越来越好的,先选一个初始模型,对抗胜率超过 80% 就以一定步长选择更新的模型进行对抗。每隔固定间隔插入 n 个 random agent 对抗,以防止 agent 局限于和自己相似的策略对抗(保证对手多样性,避免 strategy collapse)
- 存在的问题
- 所有地图联合训练,拟合难度太高
- 几乎没有做 reward shaping,奖励太稀疏
- 动作空间离散化虽然能加快训练,但可能损害性能
1.2.2 第四名队伍
-
使用的 tricks:
- 模仿学习(BC): 模仿学习本身是以 “在没有 Reward Function 的情况下,利用专家示范学一个好策略” 为出发点而建立的一个研究领域,在强化的背景下看,如果你用 IL 来给 RL 做 warm-up(就像 AlphaGo 那样),那么 IL 确实可以算一种 tricks(事实上该队伍原本的想法也确实是要后续接一个 PPO,但是由于时间问题只做到 IL 就结束了)。作者开发了一个 UI 界面,手动执行并采集一些 ( s , a ) (s,a) (s,a) 二元组作为专家数据,然后直接跑了一个最简单的行为克隆(BC)算法获得转向策略(就是直接用 s 作为样本,对应的 a 作为标签,做监督学习)
- 硬编码的能量策略:作者认为如果一开始就用最大速度冲出去,且能在高速下保持好方向,那么对手就可能被甩在后面干扰不到你,无需考虑对抗。因此使用手动设计的能量分配策略:开局最大能量加速;能量耗尽后,维持加速度和能量恢复速率相同,直到终点
-
分析:在难以收集大量数据的情况下,仅仅做了一个最简单的 BC 就能拿到第 4 名,这个还是有点出乎意料,不过仔细思考一下可以发现,这个环境中 IL 其实取巧了
- 由于本题中局部观测特性,难以获得很好的状态特征表示,使用模仿学习可以大大增强模型早期的表现

比如如果早期没有学好箭头的含义,则上面左图 agent 可能错误地转向左边,右图 agent 可能一直绕圈,使用模仿学习都能避免这些问题;另外有些地图没有箭头提示,这时沿着边缘走比较好,专家可以给出相应的指导让 agent 学会这一点;还可以用来初始化强化学习进一步优化 - BC 方法最大的问题是 distribution shift 和 mismatch,因为给予示范信息的状态分布和 agent 真实遇到的状态分布不可能完全相同,一旦 agent 处于没有示范的状态区域,它执行的动作就可能很糟糕,这很可能使 agent 进一步远离示范区域引发恶性循环
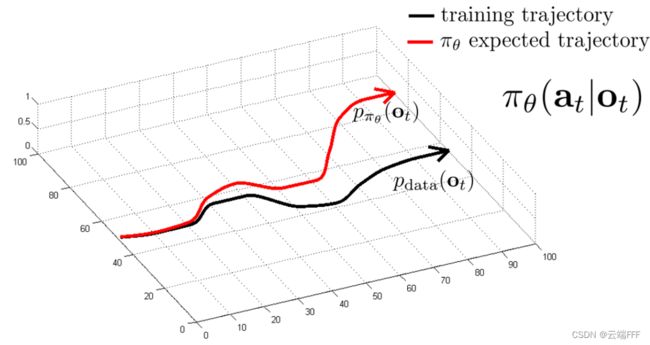
在本赛题中,可以发现状态空间是比较小的,而且 agent 有弹性,这样一方面示范可以覆盖较大范围,另一方面 agent 偏离道路时容易弹回道路中间的有示范区域,缓解了 distribution shift 和 mismatch;另外,如果人类专家在给出示范时就专门收集一些很差位置(比如路径边缘和犄角旮旯)的指导,也有助于 agent 始终保持在有示范区域,缓解上述问题
- 由于本题中局部观测特性,难以获得很好的状态特征表示,使用模仿学习可以大大增强模型早期的表现
1.2.3 第三名队伍
- 使用的 tricks:
- 更好的 reward shaping: reward = 终点奖励(原始) + 近似测地线距离奖励(到终点距离缩短加分,增长扣分) + 撞墙惩罚
- self-play:先单人训练,收敛后再随机采样 50% 胜率的对手进行训练(如果对手胜率太小学学不到东西,如果对手太强可能越学越乱(奖励太稀疏))
- 额外规则:由于起点位置固定,使用前几帧就能判断是那一张训练训练地图,这种情况下
- 在部分初始不会碰撞的情况下(如初始几步,或一些轨迹不交叉的地图)使用硬编码动作
- 部分地图加上固定加速度(避免提前耗光体力),RL agent 仅控制角加速度
- 存在的问题
- 仍然只用当前观测提取特征作为状态,没有利用历史数据构造更好的状态特征,这样泛化性能会很差
1.3 小结
-
表现较好的 Learning-based 方法基本遵循以下思路
- 选择 PPO 模型,实现较简单,且对超参数和奖励设置比较鲁棒
- 最大限度从局部观测中提取信息做 reward shaping
- self-play 提高 agent 的对抗性能;或者尽量和对手保持距离来避免对抗
- 考虑到地图和环境性质,各地图单独训练对应的最优策略,按照一定的硬编码规则切换
- 对于无法提取指导信息的部分,使用硬编码规则(比如这里的能量分配策略)
- 引入专家样本,用 IL 做 warn-up,给 RL 训提供更好的起点
-
本次比赛中 Learning-based 方法的统一问题在于
- 没有队伍针对 POMDP 的特点做针对性处理,每个时刻的局部观测蕴含的信息量太少,如果不能联合考虑历史观测数据,agent 位置、速度、能量等重要信息都无从获取,这样学到的策略就很难泛化,不说新地图,即使在训练地图间都泛化都很差(联合训练性能不如各个地图独立训练)
- 如果训练地图很有代表性,上面这样把 POMDP 当作普通的 MDP 问题硬做也是可以的,但这里各个地图间差异很大,所以 RL 方法都效果不佳(最简单的纯 IL 方法甚至都能排第 4)
2. Rule based 方法
-
Rule-based 方法说白了就是人工设计一套规则,将观测输入直接映射到输出动作。看到红灯停车,看到绿灯起步就是一种规则系统
-
放到机器学习的语境下,这大概可以相当于结合先验知识做了一个很强的特征工程(或者说数据预处理),直接替代整个学习过程
- 以图像处理分类问题为例
- 普通监督学习先做特征工程提取图像特征,然后跑监督学习算法学习从特征到预测标记的映射;
- Rule-based 直接手工设计一个分类规则作为从原始图像到预测标记的映射(PCA 降维人脸识别大概可以算这一卦的)
- 如果是放在本赛题这样的强化学习背景中
- 普通强化学习方法在每一步都对原始观测做特征工程提取特征作为状态,通过大量交互建立起各个状态的价值估计,再依赖价值估计不断优化策略,最终得到从状态到动作的映射
- Rule-based 方法直接手工设计一个规则作为从原始观测到动作的映射
-
本节仅对冠军方案进行分析说明,第二名的规则方法不提
2.1 规则设计(特征工程)
2.1.1 分析
-
深入分析 agent 的状态信息,特别是因 POMDP 而缺失的部分
- 角度可以直接积分计算
- 速度和位置难以积分计算,因为有随机碰撞
如果能获取自身的位置,就能估计一切
- 速度用位置变化估计
- 能量用当前速度和力累加估计
-
发现获取 agent 的绝对位置是重中之重,作者注意到每一帧旋转角度最多 30 度运动距离有限,这样两帧之间就会有很大重叠,直接 for 循环暴力匹配一定范围内的整数位移,就能得到 agent 每一帧的位移信息,进而可以直接积分得到绝对位置
-
更进一步,如果能得到每一帧的位移,那么我们其实可以把每一帧的观测都拼接起来还原当前的地图,从而方便地估计位置、速度、能量等关键状态信息,还可以对箭头方向、道路边缘、终点线等各种信息进行识别,这种情况下
- 利用这些信息可以大幅提高 RL 的性能
- 既然已知地图,不如直接规划出前进路线
2.1.2 冠军方案思路
-
冠军方案思路
- agent 运动过程中,不断拼接重建地图,注意两点
- 对图像进行超分,放大到 50*50,提高准确度
- 考察位移时,和当前已经重建的地图整体进行匹配,这样就能从期望上抵消掉拼接误差
- BFS 寻找地图上的出口和路径,识别箭头位置及其指向
- 综合考虑 agent 当前位置、箭头指向、距离、所需转向角度等各种信息,选择一个目标出路方向前行(核心规则)
- 转弯时增加角度补偿,提前转弯
- 硬编码能量分配措施:力*速度 = 400(这是每帧恢复值),保证能量不会耗尽
- agent 运动过程中,不断拼接重建地图,注意两点
-
地图拼接效果:下面展示了绿色 agent 在 map8 和 map11 运动过程中的地图重建情况


- 最右是当前绿色agent 所在位置
- 最左是当前绿色agent 使用历史观测拼接的地图
- 中间对左边图做了反色处理,注意在地图边缘有一些彩色点,这些是用 bfs 找出的目前所有可通行边;再看 agent 位置还有一条地图内的线,它是绿色agent去往当前目标边的 bfs 路线。相同颜色的点属于同一条边,颜色深浅表示 bfs 过程中的先后关系
2.2 规则构造细节(特征构造方法)
- 本节首先说明一些基础设置,然后说明几个关键的规则构造方法,其他没有介绍的请查看复现代码注释
- 以下用 “global map” 代表实时拼接的地图
2.2.1 基础设定
- 以下设置对于理解程序非常重要,必须加以说明
-
拼接正方向:上面两张最右侧图像都是游戏画面逆时针旋转 90 度所得,画面中的绿色和紫色方框代表两个 agent 的观测信息,注意原始观测是 agent 当前位置正前(上)方的一个正方形区域。作者把 agent 初始朝向转 180 度作为拼接地图的正方向,也就是说 agent 初始指向在构造的 global map 中总是垂直向下的,上面两个地图中 agent 都是在游戏画面水平向左起步,所以原始地图的左方变成了构造 global map 的下方,像上面那样将原始游戏画面逆时针旋转 90 度即可对齐
-
agent 尺寸和观测尺寸:超分后观测矩阵边长 50 像素,根据游戏画面比例,agent 示意圆形半径为 5 像素
-
地图尺寸:各个地图尺寸不同,为了保证地图总能拼接完整,global map 尺寸为边长 2000 像素的正方形,这远远大于所有测试地图
-
坐标系:程序涉及两个坐标系,如下所示
其中浅蓝色代表 global map,绿色圆和方框代表初始时刻 agent 及其观测的位置
- 初始时刻 agent 中心位置:中心坐标 ( 0 , 0 ) (0,0) (0,0),绝对坐标 ( 1000 , 1000 ) (1000,1000) (1000,1000)
- 初始时刻观测中心位置:中心坐标 ( 30 , 0 ) (30,0) (30,0),绝对坐标 ( 1030 , 1000 ) (1030,1000) (1030,1000)
-
角度:程序中所有角度都是测算的目标向量和 x 轴负方向的夹角,并且限制在 [-180,180] 范围内,因此初始时刻 agent 的绝对角度为 180 度或 -180 度,以此为初始值对 agent 每个动作的选择角度积分,即可得到任意时刻 agent 的绝对角度,这对于拼接地图非常重要
-
箭头指向:作者假设地图中箭头只可能有四个指向,程序中用东南西北表示,在 global map 中表示如下
-
2.2.2 包装原始观测
- 代码中的
wrap_obs函数:输入为shape = (25,25)的原始观测- resize 到 ( 25 , 25 , 4 ) (25,25,4) (25,25,4),每个像素绑定一个四维向量,前三维构成一个 one-hot 向量表示像素属性(arrow/wall/endline),根据属性不同对第四维赋值 60/90/120。后面检测箭头和可行边时,可以像
global_map[:,:,0]这样取出相应的观测标记切片进行分析 - 双线性插值放大到 ( 50 , 50 , 4 ) (50,50,4) (50,50,4),注意到插值超分会导致模糊,上面的 one-hot 向量和 60/90/120 这些值都会被模糊化,后面检测箭头和可行边时需要注意
- 根据 agent 当前的绝对角度进行旋转,对齐 global map 以便拼接
- resize 到 ( 25 , 25 , 4 ) (25,25,4) (25,25,4),每个像素绑定一个四维向量,前三维构成一个 one-hot 向量表示像素属性(arrow/wall/endline),根据属性不同对第四维赋值 60/90/120。后面检测箭头和可行边时,可以像
2.2.3 识别箭头
- 代码中的
add_arrows函数:输入为包装后观测的第 0 维度(arrow标记)切片,记为img- 遍历所有像素,由于超分导致图像模糊,只要
img[i,j]> 0.9就认为找到了一个箭头像素 - 从这个箭头像素开始 bfs,把这个箭头的所在的范围找出来
- 先从南到北按行(x)扫描箭头范围,每一行中从东到西按列(y)扫描,如果发现箭头像素出现两次,说明扫描到箭头的两个尾巴,此箭头一定是南或北指向;反之一定是东或西指向
- 对比箭头两个端点和顶点位置,通过位置关系判断箭头出箭头的具体指向
- 考察新箭头中点和过去记录所有某个箭头中点的距离,如果有太近的就认为是图像抖动所致,反之判断为新箭头进行记录
- 二重遍历,两两比较所有箭头,如果顶点距离 <60(认为是相邻箭头)且
ll箭头在k箭头所指方向(意味着已经按k箭头指向走向并看到了下一个箭头),则设置k箭头为 “已经过箭头”,否则将其记为 “有效箭头” - 回到第一步继续遍历找出其他箭头,直到本帧观测内所有箭头都找出为止
- 遍历所有像素,由于超分导致图像模糊,只要
2.2.4 找出所有可行边和目标边
- 代码中的
get_edges函数:输入为当前重建的 global map- 从 agent 当前位置开始 bfs 遍历整个 global map,这里 bfs 步进值为 3 像素,以提高效率
- 在遍历过程中考察墙壁标记切片
global_map[:,:,1]找出这个切片的所有探索边界点,存入edge_point_list,这些点都是 agent 可以前往的(没有被墙挡住) - bfs 过程中的每一步,都用
past_x和past_y记录相邻的上一个 bfs 点的坐标,这样对与任意一个点,都能通过反复查询这两个数组找出其 bfs 路径 - 遍历
edge_point_list中的每一个点,步进值 3 做 bfs,把edge_point_list切分为若干长度不超过 20 的 bfs 路径,并且排除掉那些长度小于等于 4 的路径。这样找出的路径都是探索边界上没有被墙壁阻挡的边,是 agent 可以前往的候选目标(如 2.1.2 节中间图像所示),将他们加入edge_list。每一条边的 “中点” 定义为组成该边的所有点坐标的均值 - 对于
edge_list中的每一条可行边,检查目前找出的所有箭头,每一个距离小于 70 且指向该边中点的有效箭头加 1 分,同时考虑 agent 去往该边中心位置的转向角扣分(转向角越小扣分越少,细节请看复现代码)和行进距离扣分(距离该边越近扣分越少,细节请看复现代码),选出一个最优的可去边 - 在组成最优边的所有点中,找出一个距离该边中心最近的点作为 “目标点”
- 用
past_x和past_y反向找出从 agent 当前位置去向目标点的 bfs 路径(如2.1.2 节中间图像所示),并返回 - 另外,如果 bfs 过程中发现了 endline 标记,则直接用
past_x和past_y找出从 agent 当前位置去向该标记点的 bfs 路径返回
2.2.5 生成动作
- 代码中的
get_action函数:输入为 2.2.4 节中找出的target_bfs_path- 对于能量分配,设置
power = 200 if self.v <= 2.01 else 200 / self.v * 2,其中self.v是利用 global map 差分计算的绝对速度。这里控制 power * speed ≤ 400 \text{power * speed} \leq 400 power * speed≤400 避免能量耗尽 - 对于转向角度,把
target_bfs_path的最后一个点(最靠近目标边中点的那个点)设为目标点向 agent 当前位置连直线,逐像素遍历,检查中间是否有墙壁,如果有墙壁阻挡,就按 bfs 顺序回退,直到找到没有阻挡的点作为 “可行目标点”,计算从当前位置去往该点的转向角度 angle - 返回计算出的
power和angle
- 对于能量分配,设置
2.2.6 转向角度补偿(提前转向)
- 代码中的
fix_action函数:输入为 2.2.5 节中生成的转向角度angle- 把 agent 当前位置和 4 步之前位置连线,计算该向量角度(和 x 轴负方向的夹角)
- 和 agent 当前绝对角度
self.angle(也是和 x 轴负方向的夹角)做差,标准化到 [ − 180 , 180 ] [-180,180] [−180,180],记为a - 如果现在去往目标点的夹角
angle在最大转向角度内(30),而过去一段时间的累计转向角度a超过最大转向角度,且速度较快,就进行补偿
new_angle = angle - a ∗ min ( abs(a) , 20 ) / 8 \text{new\_angle} = \text{angle - a}*\min\big(\text{abs(a)},20\big)/8 new_angle=angle - a∗min(abs(a),20)/8 - 把补偿后的转向角度限制在规定范围内( [ − 30 , 30 ] [-30,30] [−30,30])返回
2.2.7 其他
- 规则构建过程中还有很多细节函数,比如 2.2.4 中的两个打分函数、判断某个点是否在箭头所指方向的函数、暴力匹配找出每一帧位移的函数等,这些部分请到我复现的源码中查看注释
2.3 实验评估
-
先看文件夹
- agent 文件夹是可选智能体,其中
- champion_raw 是冠军方法源码
- my 是我复现的冠军方法
- random 是随机策略 agent
- rl 是官方提供的 PPO agent 示例
- assert 文件夹是说明图片
- env 文件夹和 olympics 文件夹都是环境引擎相关代码
- rl_trianer 文件夹是官方 PPO 的 RL 训练脚本
- utils 文件夹是工具函数
- Experiment 文件夹是实验 gif,详见 2.3.2 节
- agent 文件夹是可选智能体,其中
-
再看根目录下的几个文件
- evaluation_local.py 是官方提供的本地测评脚本
- run_log.py 是官方提供的测评仿在线测评脚本,这个和网站上的策略逻辑基本一致
- main.py 是我编写的本地测评脚本(直接运行这个就可以了)
2.3.1 复现冠军方案
-
体会冠军队方案的编程技巧:这个代码写得非常糟糕,堪称屎山,其具有以下问题
- 内聚程度太高,好几个函数长度超过 100 行,看不下去
- 变量命名规范不统一,比如像素坐标变量,每个地方都不太一样;变量名标识不清晰,有
a b c d这样的变量,理解困难 - 注释极少,无文档,看的时候一直在猜测他在干什么
- 缺少 2.2.1 节这样的基础设定说明,完全不知道程序的具体表现
- 大量冗余代码根本没有实际作用,该队伍应该尝试过用 global map 的附加信息跑一个 RL 方法但是最后没做完,这些遗留的部分都没有删除;另外在它实现的规则方法中也有很多冗余的变量和函数,非常影响理解
针对这些问题,我使用以下手段阅读
- 先研究明白环境模拟器的使用方法
- 单步调试,摸清模拟器如何与冠军方法交互的,搞明白冠军方法内部的运行顺序和调用关系
- 针对难以理解的代码,将他复制出来单独运行,了解其功能
- 首先理清 2.2.1 节这样的基础设定,这样才能明白代码的具体行为
- 写了一个绘图函数,看不懂的地方在 global map 上可视化出来(比如 2.1.2 图像中的可行边和目标路径),方便理解
- 硬看
-
说实话,我没感受到作者用了什么编程技巧,这种规则类方法不像机器学习那种代码有一定的框架和套路,就是一个纯粹的像素级别的逻辑处理,这种情况下确实也很难用一些技巧了,就全部都是业务逻辑。在有限的比赛时间内,写成这样乱七八槽也能理解。硬要说的话,我深刻地感受到了写注释和文档的重要性,并且对于不规范的编程习惯的厌恶更上一层楼
我选择 RL 题目原本是想学习一下怎么编写 DRL 的代码的,没想到第一名却不是 RL 方法,阅读和复现的过程中,我感觉这全部都是 dirty work,就好像在写一个巨复杂的 CSP 模拟题,完全没有通用性,在浪费大量时间后,终于怀着极大的痛苦把他搞完了。做这件事让我感到筋疲力尽,唯一的好处就是阅读代码能力可能提高了一点…
-
怀着对这个冠军代码的极大恶意,我复现时特别注意变量名规范,并且使用 python 3 新引入的函数注释方法,仿照 request 开源库的格式,给每一个函数都写了非常详细的文档说明,还对可能产生困惑的地方使用中文进行补充注释,例如
def update_map(self, wrap_obs, pos_x, pos_y) -> None: """ Splice current wrapped observation to update the global map :param wrap_obs: wrapped observations, shape = (50,50,4) :param pos_x: the x center coord of current observation center :param pos_y: the y center coord of current observation center :return: None :note: The part that has been spliced won't be overwritten """ # 观测中心的中心坐标,向上取整 x = int(pos_x + 0.5) y = int(pos_y + 0.5) # 遍历 wrap_obs 中所有像素,拼接到 self.global_map 上 for i in range(scaled_size): for j in range(scaled_size): absolute_x = to_absolute_coord(x + i - scaled_size // 2) absolute_y = to_absolute_coord(y + j - scaled_size // 2) # 这个条件限制已经拼接过的部分不要被覆盖 if wrap_obs[i, j, 3] >= 0 and self.global_map[absolute_x, absolute_y, 3] >= 150: self.global_map[absolute_x, absolute_y] = wrap_obs[i, j]现在一切都非常清晰了
-
对于逻辑层面,我复现过程中基本没有改动,因为这些逻辑本身也没什么可以改的,非要换一种写法的话,就是 “为了复现而复现” 了
2.3.2 性能评估
-
做性能评估时也遇到了很多麻烦,因为及第平台上这个比赛科目的在线测评系统一直开放,所以我一开始是打算用它来测评的,但是遇到两个问题
- 4 月 25 日,及第平台在未公式的情况下修改了环境模拟引擎,导致所有科目的观测发生变化,过去的算法和策略表现异常。这里困扰我很久,因为我发现即使上传了冠军的开源代码,其性能也非常差劲,和本地测评完全不同,一直在怀疑是不是环境模拟器的用法不对或者上传时没有遵循要求。浪费大量时间后,我仔细检查了平台上冠军方法的对抗记录,发现 4 月 25 日后其行为突然开始异常,再去看了及第平台的 git,发现 4 月 25 有一次对该类科目的 commit,故怀疑其修改了测评方式,联系平台官方人员查证后才得知确实有引擎改动,我提出的这个问题使得平台专门进行了回滚
- RL 算法由于要和环境交互,测评特别费时,及第平台上有几十个 RL 科目,所以他们使用了一个测评队列来做评估。对于这种不在比赛的科目,代码提交后,会和所有其他科目的 agent 一起排队等待测评,往往一天下来也只能跑二十场测试,这实在太慢了
-
考虑到上述问题,我决定直接写个本地测评脚本,让我复现的 agent 和原始冠军 agent 进行对抗,这样只要胜率保持在 50% 即可说明复现成功。测试时每张地图对抗 100 局,然后交换出发位置再对抗 100 局,11 张地图一共对抗 2200 局,用时 15 小时左右,我复现的 agent 胜率如下
map1 map2 map3 map4 map5 map6 map7 map8 map9 map10 map11 绿色位置出发 100% 平 100% 胜 100% 胜 100% 负 100% 胜 100% 胜 100% 负 100% 胜 100% 胜 100% 负 100% 负 紫色位置出发 100% 平 100% 负 100% 负 100% 胜 100% 负 100% 负 100% 胜 100% 负 100% 负 100% 胜 100% 胜 综合胜率 50% 50% 50% 50% 50% 50% 50% 50% 50% 50% 50% 实验说明复现 agent 具有和原始冠军 agent 完全一致的性能
经过测试发现,由于两个 agent 的行为策略完全相同,导致胜负的唯一因素就是出发时的位置,第一个弯道走在内线的 agent 必胜
-
我对 11 张地图上的比赛各制作了一张 gif(三倍速播放),放在根目录的 Experience 文件夹中,由于使用固定策略且二者规则一致,事实上所有实验都是高度相似的,gif 中的两个 agent 的轨迹都可以看做复现 agent 从相应位置出发的运动轨迹
3. 分析和改进
3.1 方案分析
- 其实前面在分析赛题和介绍 Learning-based 方法原理的过程中已经融合了不少分析了,这里再总结一下
- Rule-based 的方法融入了很多高级先验知识,比如箭头方向代表通路,又比如应该向开口方向运动,这些在 RL 方法中都要靠反复试错来学习。而且这些高级先验知识抽象程度更高,因此泛化性更好
- 考虑到地图重建的效果很好,纯 RL 方法超越冠军方案应该很困难
- 但另一方面,现在冠军方案的规则设计也不是完美无缺,比如
- map3 中如果靠左起步,就会在 T 字路口处转向错误的方向(见 gif),这是因为 2.2.4 节中介绍的
get_edges函数里,寻找目标边的标准设计不是很好。作者在这里综合考虑了箭头、距离和转向角度三个因素,但是我没看出来作者在平衡这几项时的依据是什么,感觉就是一点点尝试最后修正得到了一些还可以的超参数,这个设定在 map3 这里就出现了问题,另外在 map6 的第一道门槛处也是如此 - 由于
get_edges函数很难设计,冠军方法在面对超宽地图时应该会表现不佳,因为这时 agent 的观测中经常没有围墙,各个方向都是可行边,get_edges受到的压力就会更大,一旦它给出错误的指向,agent 就会绕很多弯路;反之,冠军方法在面对窄地图时表现应该比较好,因为这时可行边数量较少,get_edges更容易指出最优边 - 识别帧间位移的
get_displacement函数是在有限的区域内做暴力搜索进行匹配的,如果 agent 出现剧烈碰撞,瞬时出现很大的位移,该函数识别的位移数据就可能出错,导致拼接的 global map 中出现断裂,这些断裂又会干扰get_edges函数的判断。不过从试验来看这种剧烈碰撞几乎不会出现 - 在 2.2.3 节介绍的箭头识别方法 add_arrows 中,假设了箭头只可能指向东南西北四个方向,但是在 map7 和 map11 中其实也出现了倾斜的箭头,这些倾斜箭头会导致
add_arrows运行出错。不过由于get_edges方法不只考虑了箭头,从试验结果看这一点小错误影响不大 - 硬编码的能量策略比较保守,agent 运动速度较慢,冠军其实是胜在稳定
- map3 中如果靠左起步,就会在 T 字路口处转向错误的方向(见 gif),这是因为 2.2.4 节中介绍的
3.2 改进展望
-
虽然 3.1 节中指出了一些问题,但是他们在冠军方案这种重建地图的框架下几乎是无解的,特别是
get_edges函数中选取目标边的规则设计是一个开放性问题,在逐步构建地图的过程中,我们无法获取去向终点最优路径的任何绝对准确的信息(map7中的箭头也可能导致一直在外侧转圈),也就只能像作者这样根据直觉设计一个基础规则,再利用已知地图不断尝试来优化它了 -
但是另一方面,我们可以尝试将 Rule-based 方法和 Learning-based 方法相结合。注意到我们可以根据前几帧的观测直接判断出当前所在的地图是哪一张训练地图,那么或许可以尝试以下方法
- 让对手不动,使用 RL 方法在各个训练地图上找出其最优策略,这里我们甚至可以作弊直接使用全局观测来训练,这样找到最优策略很容易
- 用找到的最优策略和环境交互,找到最优轨迹,将其对应的最优动作序列存储起来
- 测试时先判断当前地图,如果是训练地图,就直接重放对应的最优动作序列;如果是未见地图,则还按这里的冠军方法运行
这个方法的唯一问题在于对手可能会和我们发生碰撞,导致重放动作序列无法还原对应的最优轨迹。不过不用太担心,我们在 0.1.2 节就分析过:这个环境的对抗不是很强,超过或落后对手一定距离即可看作没有对手存在,RL 学到的能量分配策略都很激进,很容易和对手拉开差距从而避免对抗。同时,我们还可以对动作重放过程进行监控,一旦偏移最优轨迹太多,就还原到这里的冠军方法
-
由于时间原因没有进行实验,但是理论上讲,上述方法应该能大幅提高 agent 的性能,至少不会比现在更差
4.总结
- 第一次深入研究一个强化学习比赛,并借此机会对 RL 的泛化性问题进行了一点研究,对 RL 有了更深刻的认识;虽然复现代码的过程非常痛苦,但也体会到了代码规范的重要性,总体上感觉还是很有意义的
- 及第 AI 这个平台不错,可以关注下