- 【笔试题汇总】华为春招笔试题题解 2024-3-20
PXM的算法星球
大厂面试题华为面试数据结构算法
这里是paoxiaomo,一个现役ACMer,之后将会持续更新算法笔记系列以及笔试题题解系列本文章面向想打ICPC/蓝桥杯/天梯赛等程序设计竞赛,以及各个大厂笔试的选手感谢大家的订阅➕和喜欢有什么想看的算法专题可以私信博主(本文题面由清隆学长收集)01.K小姐的魔法药水问题描述K小姐是一位魔法师,她最近在研究一种神奇的魔法药水。这种药水由一系列魔法材料制成,每种材料都有一个正整数的魔法值。K小姐按
- java将json字符串转换成对象,看这篇足矣了!
imtokenmax合约众筹
程序员面试经验分享java
20个二叉树面试高频0.几个概念1.求二叉树中的节点个数2.求二叉树的最大层数(最大深度)3.先序遍历/前序遍历4.中序遍历5.后序遍历6.分层遍历7.求二叉树第K层的节点个数8.求二叉树第K层的叶子节点个数9.判断两棵二叉树是否结构相同10.判断二叉树是不是平衡二叉树11.求二叉树的镜像12.求二叉树中两个节点的最低公共祖先节点13.求二叉树的直径14.由前序遍历序列和中序遍历序列重建二叉树15
- HDU2196Computer 树形dp
Vibrant
传送门解法1树的直径参考博客#include//树的直径#defineMAXN10010usingnamespacestd;typedefpairP;intdis[MAXN],Max,root;vectora[MAXN];voidInit(intn){Max=0;for(inti=1;iMax)Max=sum,root=now;for(inti=0;i//记忆化搜索#defineMAXN10010
- 动态规划的时间复杂度优化
闻缺陷则喜何志丹
#算法基础数据结构与算法动态规划算法c++LeetCode状态转移状态表示逆向思考
作者推荐视频算法专题本文涉及知识点动态规划汇总优化动态规划的时间复杂度,主要有如下几种:一,不同的状态表示。比如:n个人,m顶帽子。第一种方式:dp[i][mask],i表示前i个人已经选择帽子,mask表示那些帽子已经选择。空间复杂度:O(n2m)。第二种方式:dp[i][mask],i表示前i个帽子已经选择,mask表示那些人已经选择。空间复杂度:O(m22)。n大,则现在方式一;否则选择方式
- 【科学刷题】完全吃透所有树相关的算法题
数学工具构造器
科学刷题算法数据结构leetcode
文章目录1二叉树1.1二叉树递归/层序遍历1.1.1二叉树的对称/翻转/镜像1.1.2二叉树的直径/最大路径和1.1.2.1二叉树的直径1.1.2.2二叉树中的最大路径和1.1.3二叉树的最大/最小深度1.1.4填充每个节点的下一个右侧节点指针1.1.5二叉树的层序遍历1.1.5.1二叉树最大宽度1.2完全二叉树1.2.1复杂度log2N\log^2Nlog2N的题目1.2.1.1完全二叉树的结
- 力扣题目训练(16)
落幕·重逢
编程学习leetcode算法c++
2024年2月9日力扣题目训练2024年2月9日力扣题目训练530.二叉搜索树的最小绝对差541.反转字符串II543.二叉树的直径238.除自身以外数组的乘积240.搜索二维矩阵II124.二叉树中的最大路径和2024年2月9日力扣题目训练2024年2月9日第十六天编程训练,今天主要是进行一些题训练,包括简单题3道、中等题2道和困难题1道。惰性太强现在才完成,不过之后我会认真完成的。530.二叉
- 算法专题:线性DP
Q天马A行空Q
算法导论算法leetcode线性DP
参考练习习题总集文章目录10.正则表达式匹配44.通配符匹配45.跳跃游戏II53.最大子数组和(LCR161连续天数的最高销售额)91.解码方法97.交错字符串115.不同的子序列119.杨辉三角II198.打家劫舍(LCR089打家劫舍)213.打家劫舍II(LCR090打家劫舍II)10.正则表达式匹配第一道题就是困难题让我很难蚌,真是磨人啊。classSolution{public:boo
- 算法专题:滑动窗口
Q天马A行空Q
算法导论算法leetcode滑动窗口
参考练习习题总集文章目录3.无重复字符的最长子串30.串联所有单词的子串76.最小覆盖子串187.重复的DNA序列219.存在重复元素II220.存在重复元素III396.旋转函数424.替换后的最长重复字符438.找到字符串中所有字母异位词滑动窗口太简单了,没啥说的自己做吧。3.无重复字符的最长子串classSolution{public:intlengthOfLongestSubstring(
- 算法专题:前缀和
Q天马A行空Q
算法导论算法leetcode前缀和
参考练习习题总集文章目录53.最大子数组和(LCR161连续天数的最高销售额)85.最大矩形187.重复的DNA序列209.长度最小的子数组238.除自身以外数组的乘积363.矩形区域不超过K的最大数值和396.旋转函数53.最大子数组和(LCR161连续天数的最高销售额)线性DPclassSolution{public:intmaxSubArray(vector&nums){for(inti=1
- 关闭Windows自动更新的6种方法
人不走空
windows
人不走空个人主页:人不走空系列专栏:算法专题⏰诗词歌赋:斯是陋室,惟吾德馨目录个人主页:人不走空系列专栏:算法专题⏰诗词歌赋:斯是陋室,惟吾德馨✔方法1.Windows设置✔方法2.关闭WindowsUpdate服务✔方法3.本地组策略编辑器✔方法4.任务计划程序✔方法5.注册表编辑器✔方法6.通过工具关闭Win10自动更新作者其他作品:这里我们将为您分享6种关闭Win10自动更新的方法,分别是通
- 【深度优先搜索】【树】【图论】2973. 树中每个节点放置的金币数目
闻缺陷则喜何志丹
#算法题深度优先图论算法c++LeetCode树金币
作者推荐视频算法专题本博文涉及知识点深度优先搜索树图论分类讨论LeetCode2973.树中每个节点放置的金币数目给你一棵n个节点的无向树,节点编号为0到n-1,树的根节点在节点0处。同时给你一个长度为n-1的二维整数数组edges,其中edges[i]=[ai,bi]表示树中节点ai和bi之间有一条边。给你一个长度为n下标从0开始的整数数组cost,其中cost[i]是第i个节点的开销。你需要在
- 12.图论1 最短路之dijkstra算法
准确、系统、简洁地讲算法
算法图论深度优先
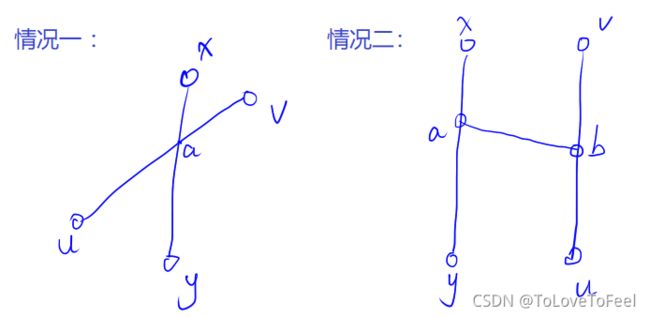
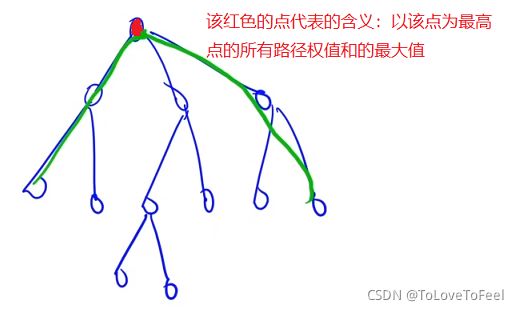
图论常见类型的图二分图判定:染色法。性质:可以二着色。无奇圈。BFS&DFS树的直径模板两遍dfs/bfs,证明时反证法的核心是用假设推出矛盾。设1是一开始随机选的点,s是与其最远的点,证明s是直径的一端。反证:假设s不是直径的一端,ss是直径的一端。现在要做的就是证明ss是直径的一端是错误的,从而不存在s的反面的情况即可完成证明。要证ss是直径的一端是错误的,那么要将ss所在的最长的径与直径比较
- Java和JavaScript区别与联系
人不走空
javascript
人不走空个人主页:人不走空系列专栏:算法专题⏰诗词歌赋:斯是陋室,惟吾德馨目录个人主页:人不走空系列专栏:算法专题⏰诗词歌赋:斯是陋室,惟吾德馨梗概:一、起源与发展二、语言特性对比六、二者详细对比六、两者示例代码七、总结作者其他作品:梗概:Java和JavaScript是两种截然不同的编程语言,尽管它们的名称相似,但它们在设计理念、语法规则、应用领域等方面有着本质的区别。Java是一种静态类型的、
- Svelte:下一代前端框架的革命性选择
人不走空
前端框架
人不走空个人主页:人不走空系列专栏:算法专题⏰诗词歌赋:斯是陋室,惟吾德馨目录个人主页:人不走空系列专栏:算法专题⏰诗词歌赋:斯是陋室,惟吾德馨1.Svelte的特点2.Svelte的优势3.Svelte的应用场景4.代码案例结语作者其他作品:Svelte是一种全新的前端框架,与传统的虚拟DOM框架不同,它采用了一种全新的编译思想,能够将组件化开发的代码在构建时转换成高效的JavaScript代码
- 【动态规划】【前缀和】【C++算法】LCP 57. 打地鼠
闻缺陷则喜何志丹
#算法题算法动态规划c++力扣前缀和打地鼠枚举位置
作者推荐视频算法专题本文涉及知识点动态规划汇总C++算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例包括课程视频LCP57.打地鼠勇者面前有一个大小为3*3的打地鼠游戏机,地鼠将随机出现在各个位置,moles[i]=[t,x,y]表示在第t秒会有地鼠出现在(x,y)位置上,并于第t+1秒该地鼠消失。勇者有一把可敲打地鼠的锤子,初始时刻(即第0秒)锤子位于正中间的格子(1,1),锤子的使用规则
- #Z2294. 打印树的直径
伟大的拜线段树jjh
数据结构
Description给你一棵树,树上有N个点,编号从0到N-1请找出任意一条树的直径,并输出直径上的点,输出顺序为从直径的某个端点走向另一个端点FormatInput第一行一个整数n;之后n-1行每行两个整数u,v,表示u和v之间有边。1usingnamespacestd;vectorvec[1000001];boolvis[10000001];intans,dep[1000001],n,x,y
- 精选力扣500题 第50题 LeetCode 543. 二叉树的直径【c++详细题解】
林小鹿@
LeetCode题解二叉树数据结构与算法力扣高频面试题
目录1、题目2、思路3、c++代码4、java代码1、题目给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。示例:给定二叉树1/\23/\45返回3,它的长度是路径[4,2,1,3]或者[5,2,1,3]。注意:两结点之间的路径长度是以它们之间边的数目表示。2、思路(递归,树的遍历)O(n)O(n)O(n)在这道题目中
- 树形dp解法
像风一样_
深度优先算法
二叉树的直径将一棵树抽象成左子树,右子树,根节点,求出左子树作为根的最长链长度l,右子树作为根的最长链长度r,则其父节点的最长链长度为max(l,r)+1/***Definitionforabinarytreenode.*structTreeNode{*intval;*TreeNode*left;*TreeNode*right;*TreeNode():val(0),left(nullptr),ri
- CF1404BTree Tag/ BZOJ0487. 树上追逐详解
伟大的拜线段树jjh
算法图论深度优先
1.题目传送门:TreeTag-洛谷2.思路我们考虑什么情况下Alice可以获胜.如果≤da,则Alice可以一步就追上Bob.如果Alice处在一个能覆盖整棵树的点,即2da+1≥树的直径,那么Bob也无论走到哪里Alice都能追到,Alice获胜.其它情况下,Alice会一步一步逼近Bob,并一定能把Bob逼近某棵子树.如果当前Alice占据一个点,使Bob无论怎么走都还在Alice的控制范围
- 【动态规划】【状态压缩】【2次选择】【广度搜索】1494. 并行课程 II
闻缺陷则喜何志丹
#算法题数据结构与算法动态规划算法c++力扣状态压缩广度优先搜索并行课程
作者推荐视频算法专题本文涉及知识点动态规划汇总状态压缩广度优先搜索LeetCode1494.并行课程II给你一个整数n表示某所大学里课程的数目,编号为1到n,数组relations中,relations[i]=[xi,yi]表示一个先修课的关系,也就是课程xi必须在课程yi之前上。同时你还有一个整数k。在一个学期中,你最多可以同时上k门课,前提是这些课的先修课在之前的学期里已经上过了。请你返回上完
- 开源软件:推动技术发展的强大引擎
人不走空
开源软件
人不走空个人主页:人不走空系列专栏:算法专题⏰诗词歌赋:斯是陋室,惟吾德馨目录个人主页:人不走空系列专栏:算法专题⏰诗词歌赋:斯是陋室,惟吾德馨开源软件的影响力一、开源软件的优势二、开源软件与技术创新三、如何更好地利用开源软件推动技术创新结语:作者其他作品:开源软件的影响力随着信息技术的快速发展,开源软件已经成为软件开发的趋势,并产生了深远的影响。开源软件的低成本、可协作性和透明度等特点,使得越来
- 【算法专题】前缀和(附图解、代码)
放风讲故事
算法
前言本文主要是前缀和的文章,如果有什么需要改进的地方还请大佬指出⛺️作者简介:大家好,我是青衿☁️博客首页:CSDN主页放风讲故事每日一句:努力一点,优秀一点目录文章目录前言**目录**1.统计范围内的元音字符串数2.二维区域和检索-矩阵不可变文章末尾1.统计范围内的元音字符串数leetcode2559给你一个下标从0开始的字符串数组words以及一个二维整数数组queries。每个查询queri
- 【算法专题】贪心算法
YoungMLet
算法专栏算法贪心算法c++leetcode开发语言
贪心算法贪心算法介绍1.柠檬水找零2.将数组和减半的最少操作次数3.最大数4.摆动序列(贪心思路)5.最长递增子序列(贪心算法)6.递增的三元子序列7.最长连续递增序列8.买卖股票的最佳时机9.买卖股票的最佳时机Ⅱ(贪心算法)10.K次取反后最大化的数组和11.按身高排序12.优势洗牌13.最长回文串14.增减字符串匹配15.分发饼干16.最优除法17.跳跃游戏Ⅱ18.跳跃游戏19.加油站20.单
- 【动态规划】【字符串】【行程码】1531. 压缩字符串
闻缺陷则喜何志丹
#算法题数据结构与算法动态规划算法c++LeetCode字符串行程码压缩
作者推荐视频算法专题本文涉及知识点动态规划汇总LeetCode1531.压缩字符串II行程长度编码是一种常用的字符串压缩方法,它将连续的相同字符(重复2次或更多次)替换为字符和表示字符计数的数字(行程长度)。例如,用此方法压缩字符串“aabccc”,将“aa”替换为“a2”,“ccc”替换为`“c3”。因此压缩后的字符串变为“a2bc3”。注意,本问题中,压缩时没有在单个字符后附加计数‘1’。给你
- 递归算法——Leetcode题型总结(1)
宛宛宛
leetcode算法二叉树
二叉树专题目录1,最长同值路径(Leetcode687题)1.1二叉树的直径(543题)2,BiNode3,二叉搜索树的范围和(938)4,二叉搜索树节点最小距离(783)1,最长同值路径(Leetcode687题)题目描述:给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。这条路径可以经过也可以不经过根节点。注意:两个节点之间的路径长度由它们之间的边数表示。示例1:输入:5/\45
- 【算法专题】动态规划综合篇
YoungMLet
算法专栏算法动态规划c++开发语言leetcode
动态规划7.01.最长公共子序列2.不相交的线3.不同的子序列4.通配符匹配5.正则表达式匹配6.交错字符串7.两个字符串的最小ASCII删除和8.最长重复子数组1.最长公共子序列题目链接->Leetcode-1143.最长公共子序列Leetcode-1143.最长公共子序列题目:给定两个字符串text1和text2,返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列,返回0。一个字符串
- 【算法专题】二分查找(入门)
放风讲故事
算法
前言本文主要是二分查找(入门)的文章,如果有什么需要改进的地方还请大佬指出⛺️作者简介:大家好,我是青衿☁️博客首页:CSDN主页放风讲故事每日一句:努力一点,优秀一点目录文章目录前言**目录**二分查找1.二分查找搜索2.在排序数组中查找元素的第一和最后一个位置文章末尾二分查找1.二分查找搜索题目链接->Leetcode-704.二分查找Leetcode-704.二分查找题目:给定一个n个元素有
- 【算法专题】二分查找(进阶)
放风讲故事
算法
前言本文主要是二分查找(进阶)的文章,如果有什么需要改进的地方还请大佬指出⛺️作者简介:大家好,我是青衿☁️博客首页:CSDN主页放风讲故事每日一句:努力一点,优秀一点目录文章目录前言**目录**二分法1.爱吃香蕉的珂珂2.在D天内送达包裹的能力文章末尾二分法二分法的特性:1,题目满足单调性2,待求解的值是0到无限的一个值1.爱吃香蕉的珂珂leetcode875珂珂喜欢吃香蕉。这里有n堆香蕉,第i
- 【算法专题】动态规划之回文子串问题
YoungMLet
算法专栏算法动态规划c++性能优化开发语言leetcode
动态规划6.0动态规划---回文子串问题1.回文子串2.最长回文子串3.分割回文串Ⅳ4.分割回文串Ⅱ5.最长回文子序列6.让字符串成为回文串的最少插入次数动态规划---回文子串问题1.回文子串题目链接->Leetcode-647.回文子串Leetcode-647.回文子串题目:给你一个字符串s,请你统计并返回这个字符串中回文子串的数目。回文字符串是正着读和倒过来读一样的字符串。子字符串是字符串中的
- 蓝桥杯真题讲解【大臣的旅费】(树的直径、DFS)
sutr
蓝桥杯深度优先职场和发展算法c++数据结构宽度优先
大臣的旅费很久以前,T王国空前繁荣。为了更好地管理国家,王国修建了大量的快速路,用于连接首都和王国内的各大城市。为节省经费,T国的大臣们经过思考,制定了一套优秀的修建方案,使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时,如果不重复经过大城市,从首都到达每个大城市的方案都是唯一的。J是T国重要大臣,他巡查于各大城市之间,体察民情。所以,从一个城市马不停蹄地到另一个城市成了J最常做的
- 戴尔笔记本win8系统改装win7系统
sophia天雪
win7戴尔改装系统win8
戴尔win8 系统改装win7 系统详述
第一步:使用U盘制作虚拟光驱:
1)下载安装UltraISO:注册码可以在网上搜索。
2)启动UltraISO,点击“文件”—》“打开”按钮,打开已经准备好的ISO镜像文
- BeanUtils.copyProperties使用笔记
bylijinnan
java
BeanUtils.copyProperties VS PropertyUtils.copyProperties
两者最大的区别是:
BeanUtils.copyProperties会进行类型转换,而PropertyUtils.copyProperties不会。
既然进行了类型转换,那BeanUtils.copyProperties的速度比不上PropertyUtils.copyProp
- MyEclipse中文乱码问题
0624chenhong
MyEclipse
一、设置新建常见文件的默认编码格式,也就是文件保存的格式。
在不对MyEclipse进行设置的时候,默认保存文件的编码,一般跟简体中文操作系统(如windows2000,windowsXP)的编码一致,即GBK。
在简体中文系统下,ANSI 编码代表 GBK编码;在日文操作系统下,ANSI 编码代表 JIS 编码。
Window-->Preferences-->General -
- 发送邮件
不懂事的小屁孩
send email
import org.apache.commons.mail.EmailAttachment;
import org.apache.commons.mail.EmailException;
import org.apache.commons.mail.HtmlEmail;
import org.apache.commons.mail.MultiPartEmail;
- 动画合集
换个号韩国红果果
htmlcss
动画 指一种样式变为另一种样式 keyframes应当始终定义0 100 过程
1 transition 制作鼠标滑过图片时的放大效果
css
.wrap{
width: 340px;height: 340px;
position: absolute;
top: 30%;
left: 20%;
overflow: hidden;
bor
- 网络最常见的攻击方式竟然是SQL注入
蓝儿唯美
sql注入
NTT研究表明,尽管SQL注入(SQLi)型攻击记录详尽且为人熟知,但目前网络应用程序仍然是SQLi攻击的重灾区。
信息安全和风险管理公司NTTCom Security发布的《2015全球智能威胁风险报告》表明,目前黑客攻击网络应用程序方式中最流行的,要数SQLi攻击。报告对去年发生的60亿攻击 行为进行分析,指出SQLi攻击是最常见的网络应用程序攻击方式。全球网络应用程序攻击中,SQLi攻击占
- java笔记2
a-john
java
类的封装:
1,java中,对象就是一个封装体。封装是把对象的属性和服务结合成一个独立的的单位。并尽可能隐藏对象的内部细节(尤其是私有数据)
2,目的:使对象以外的部分不能随意存取对象的内部数据(如属性),从而使软件错误能够局部化,减少差错和排错的难度。
3,简单来说,“隐藏属性、方法或实现细节的过程”称为——封装。
4,封装的特性:
4.1设置
- [Andengine]Error:can't creat bitmap form path “gfx/xxx.xxx”
aijuans
学习Android遇到的错误
最开始遇到这个错误是很早以前了,以前也没注意,只当是一个不理解的bug,因为所有的texture,textureregion都没有问题,但是就是提示错误。
昨天和美工要图片,本来是要背景透明的png格式,可是她却给了我一个jpg的。说明了之后她说没法改,因为没有png这个保存选项。
我就看了一下,和她要了psd的文件,还好我有一点
- 自己写的一个繁体到简体的转换程序
asialee
java转换繁体filter简体
今天调研一个任务,基于java的filter实现繁体到简体的转换,于是写了一个demo,给各位博友奉上,欢迎批评指正。
实现的思路是重载request的调取参数的几个方法,然后做下转换。
- android意图和意图监听器技术
百合不是茶
android显示意图隐式意图意图监听器
Intent是在activity之间传递数据;Intent的传递分为显示传递和隐式传递
显式意图:调用Intent.setComponent() 或 Intent.setClassName() 或 Intent.setClass()方法明确指定了组件名的Intent为显式意图,显式意图明确指定了Intent应该传递给哪个组件。
隐式意图;不指明调用的名称,根据设
- spring3中新增的@value注解
bijian1013
javaspring@Value
在spring 3.0中,可以通过使用@value,对一些如xxx.properties文件中的文件,进行键值对的注入,例子如下:
1.首先在applicationContext.xml中加入:
<beans xmlns="http://www.springframework.
- Jboss启用CXF日志
sunjing
logjbossCXF
1. 在standalone.xml配置文件中添加system-properties:
<system-properties> <property name="org.apache.cxf.logging.enabled" value=&
- 【Hadoop三】Centos7_x86_64部署Hadoop集群之编译Hadoop源代码
bit1129
centos
编译必需的软件
Firebugs3.0.0
Maven3.2.3
Ant
JDK1.7.0_67
protobuf-2.5.0
Hadoop 2.5.2源码包
Firebugs3.0.0
http://sourceforge.jp/projects/sfnet_findbug
- struts2验证框架的使用和扩展
白糖_
框架xmlbeanstruts正则表达式
struts2能够对前台提交的表单数据进行输入有效性校验,通常有两种方式:
1、在Action类中通过validatexx方法验证,这种方式很简单,在此不再赘述;
2、通过编写xx-validation.xml文件执行表单验证,当用户提交表单请求后,struts会优先执行xml文件,如果校验不通过是不会让请求访问指定action的。
本文介绍一下struts2通过xml文件进行校验的方法并说
- 记录-感悟
braveCS
感悟
再翻翻以前写的感悟,有时会发现自己很幼稚,也会让自己找回初心。
2015-1-11 1. 能在工作之余学习感兴趣的东西已经很幸福了;
2. 要改变自己,不能这样一直在原来区域,要突破安全区舒适区,才能提高自己,往好的方面发展;
3. 多反省多思考;要会用工具,而不是变成工具的奴隶;
4. 一天内集中一个定长时间段看最新资讯和偏流式博
- 编程之美-数组中最长递增子序列
bylijinnan
编程之美
import java.util.Arrays;
import java.util.Random;
public class LongestAccendingSubSequence {
/**
* 编程之美 数组中最长递增子序列
* 书上的解法容易理解
* 另一方法书上没有提到的是,可以将数组排序(由小到大)得到新的数组,
* 然后求排序后的数组与原数
- 读书笔记5
chengxuyuancsdn
重复提交struts2的token验证
1、重复提交
2、struts2的token验证
3、用response返回xml时的注意
1、重复提交
(1)应用场景
(1-1)点击提交按钮两次。
(1-2)使用浏览器后退按钮重复之前的操作,导致重复提交表单。
(1-3)刷新页面
(1-4)使用浏览器历史记录重复提交表单。
(1-5)浏览器重复的 HTTP 请求。
(2)解决方法
(2-1)禁掉提交按钮
(2-2)
- [时空与探索]全球联合进行第二次费城实验的可能性
comsci
二次世界大战前后,由爱因斯坦参加的一次在海军舰艇上进行的物理学实验 -费城实验
至今给我们大家留下很多迷团.....
关于费城实验的详细过程,大家可以在网络上搜索一下,我这里就不详细描述了
在这里,我的意思是,现在
- easy connect 之 ORA-12154: TNS: 无法解析指定的连接标识符
daizj
oracleORA-12154
用easy connect连接出现“tns无法解析指定的连接标示符”的错误,如下:
C:\Users\Administrator>sqlplus username/
[email protected]:1521/orcl
SQL*Plus: Release 10.2.0.1.0 – Production on 星期一 5月 21 18:16:20 2012
Copyright (c) 198
- 简单排序:归并排序
dieslrae
归并排序
public void mergeSort(int[] array){
int temp = array.length/2;
if(temp == 0){
return;
}
int[] a = new int[temp];
int
- C语言中字符串的\0和空格
dcj3sjt126com
c
\0 为字符串结束符,比如说:
abcd (空格)cdefg;
存入数组时,空格作为一个字符占有一个字节的空间,我们
- 解决Composer国内速度慢的办法
dcj3sjt126com
Composer
用法:
有两种方式启用本镜像服务:
1 将以下配置信息添加到 Composer 的配置文件 config.json 中(系统全局配置)。见“例1”
2 将以下配置信息添加到你的项目的 composer.json 文件中(针对单个项目配置)。见“例2”
为了避免安装包的时候都要执行两次查询,切记要添加禁用 packagist 的设置,如下 1 2 3 4 5
- 高效可伸缩的结果缓存
shuizhaosi888
高效可伸缩的结果缓存
/**
* 要执行的算法,返回结果v
*/
public interface Computable<A, V> {
public V comput(final A arg);
}
/**
* 用于缓存数据
*/
public class Memoizer<A, V> implements Computable<A,
- 三点定位的算法
haoningabc
c算法
三点定位,
已知a,b,c三个顶点的x,y坐标
和三个点都z坐标的距离,la,lb,lc
求z点的坐标
原理就是围绕a,b,c 三个点画圆,三个圆焦点的部分就是所求
但是,由于三个点的距离可能不准,不一定会有结果,
所以是三个圆环的焦点,环的宽度开始为0,没有取到则加1
运行
gcc -lm test.c
test.c代码如下
#include "stdi
- epoll使用详解
jimmee
clinux服务端编程epoll
epoll - I/O event notification facility在linux的网络编程中,很长的时间都在使用select来做事件触发。在linux新的内核中,有了一种替换它的机制,就是epoll。相比于select,epoll最大的好处在于它不会随着监听fd数目的增长而降低效率。因为在内核中的select实现中,它是采用轮询来处理的,轮询的fd数目越多,自然耗时越多。并且,在linu
- Hibernate对Enum的映射的基本使用方法
linzx0212
enumHibernate
枚举
/**
* 性别枚举
*/
public enum Gender {
MALE(0), FEMALE(1), OTHER(2);
private Gender(int i) {
this.i = i;
}
private int i;
public int getI
- 第10章 高级事件(下)
onestopweb
事件
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- 孙子兵法
roadrunners
孙子兵法
始计第一
孙子曰:
兵者,国之大事,死生之地,存亡之道,不可不察也。
故经之以五事,校之以计,而索其情:一曰道,二曰天,三曰地,四曰将,五
曰法。道者,令民于上同意,可与之死,可与之生,而不危也;天者,阴阳、寒暑
、时制也;地者,远近、险易、广狭、死生也;将者,智、信、仁、勇、严也;法
者,曲制、官道、主用也。凡此五者,将莫不闻,知之者胜,不知之者不胜。故校
之以计,而索其情,曰
- MySQL双向复制
tomcat_oracle
mysql
本文包括:
主机配置
从机配置
建立主-从复制
建立双向复制
背景
按照以下简单的步骤:
参考一下:
在机器A配置主机(192.168.1.30)
在机器B配置从机(192.168.1.29)
我们可以使用下面的步骤来实现这一点
步骤1:机器A设置主机
在主机中打开配置文件 ,
- zoj 3822 Domination(dp)
阿尔萨斯
Mina
题目链接:zoj 3822 Domination
题目大意:给定一个N∗M的棋盘,每次任选一个位置放置一枚棋子,直到每行每列上都至少有一枚棋子,问放置棋子个数的期望。
解题思路:大白书上概率那一张有一道类似的题目,但是因为时间比较久了,还是稍微想了一下。dp[i][j][k]表示i行j列上均有至少一枚棋子,并且消耗k步的概率(k≤i∗j),因为放置在i+1~n上等价与放在i+1行上,同理