【自用】【持续更新】LaTeX常用基础语法大全

LaTeX常用基础语法大全

段落

居中

\begin{center}
要居中的内容
\end{center}

排序列表

% 原始模板
\begin{enumerate}
\item 第一小题
\item 第二小题
\end{enumerate}
% 自定义排序列表的编号形式
\begin{enumerate}[(1)]
\item 第一小题
\item 第二小题
\end{enumerate}
\begin{enumerate}[a.]
\item 第一小题
\item 第二小题
\end{enumerate}
\begin{enumerate}[a)]
\item 第一小题
\item 第二小题
\end{enumerate}
% 实心圆点列表
\begin{itemize}
	\item 第一小题
	\item 第二小题
\end{itemize}
% 短横杠列表
\begin{itemize}
	\item[-] 第一小题
	\item[-] 第二小题
\end{itemize}

文本、变量

加粗

\textbf{A}、\boldsymbol{A}、\boldsymbol{我们}、\textbf{我们}、我们

$\text{A}、\mathbf{A}、\mathbf{我们}、\text{我们}、我们$

斜体

\textit{我们}、\it{我们}

$\text{我们}、我们$

向量（顶有向量箭头→）

\vec v

$v$

估计（顶有尖头hat）

\hat{y}

$\hat{y}$

平均（顶有横线）

% \overline的线稍长，能覆盖所有字符
\bar x ，\overline x，\bar{AB} ，\overline{AB}

$\bar{x}，\overline{x}，\overline{AB}，\overline{AB}$

顶有波浪号~

% \widetilde能覆盖所有字符
\tilde x ，\widetilde x，\tilde{AB} ，\widetilde{AB}

$\tilde{x}，x，\widetilde{AB}，AB$

分式

\frac{分子}{分母}

$\frac{2}{3},\frac{x+y}{2}$

24个希腊字母

时不时就会用到几个，干脆全部打一遍，并标明音标（防止会写不会读）
注：大写只用把首字母大写即可。$\phi 和\epsilon$从语法上看虽然是变体，但更常用，因此标明。

小、大写	语法	音标	小、大写	语法	音标
$\alpha \mathrm{A}$	\alpha\Alpha	/'ælfə/	$\nu \mathrm{N}$	\nu\Nu	/nju:/
$\beta \mathrm{B}$	\beta\Beta	/'beɪtə/	$\xi \Xi$	\xi\Xi	希腊/ksi/(一般读这个) 英美 /ˈzaɪ/ 或 /ˈsaɪ/
$\gamma \Gamma$	\gamma\Gamma	/'gæmə/	$o\mathrm{O}$	\omicron\Omicron	/əuˈmaikrən/ 或 /ˈɑmɪˌkrɑn/
$\delta \Delta$	\delta\Delta	/'deltə/	$\pi \Pi$	\pi\Pi	/paɪ/
$ϵ\epsilon \mathrm{E}$	\epsilon\varepsilon\Epsilon	/'epsɪlɒn/艾普西隆	$\rho \mathrm{P}$	\rho\Rho	/rəʊ/
$\zeta \mathrm{Z}$	\zeta\Zeta	/'zi:tə/	$\sigma \Sigma$	\sigma\Sigma	/'sɪɡmə/
$\eta \mathrm{H}$	\eta\Eta	/'i:tə/	$\tau \mathrm{T}$	\tau\Tau	/tɔ:/ 或 /taʊ/
$\theta \Theta$	\theta\Theta	/'θi:tə/	$\upsilon {\rm Y}$	\upsilon\Upsilon	/ˈipsɪlon/ 或 /ˈʌpsɪlɒn/厄普西隆
$\iota \mathrm{I}$	\iota\Iota	/aɪ’əʊtə/	$\varphi \phi \Phi$	\phi\varphi\Phi	/faɪ/
$\kappa \mathrm{K}$	\kappa\Kappa	/'kæpə/	$\chi \mathrm{X}$	\chi\Chi	/kaɪ/
$\lambda \Lambda$	\lambda\Lambda	/'læmdə/	$\psi \Psi$	\psi\Psi	/psaɪ/
$\mu \mathrm{M}$	\mu\Mu	/mju:/	$\omega \Omega$	\omega\Omega	/'əʊmɪɡə/ 或 /oʊ’meɡə/

花体、集合手写体

% 花体
\mathcal{X} ，\mathcal{Y} ，\mathcal{D}
% 集合手写体
\mathbb{N} ，\mathbb{Z} ，\mathbb{R} ，\mathbb{C} ，\mathbb{Q}

$\mathcal{X}，\mathcal{Y}，\mathcal{D}$
常常在板书上看到这样的集合手写体。\mathbb也就是Blackboard bold，为什么要这么写
$\mathbb{N}，\mathbb{Z}，\mathbb{R}，\mathbb{C}，\mathbb{Q}$

大型运算

求和

$\sum_{i=1}^{n}x_i$  # 上下标在右边
$\sum\limits_{i=1}^{n}x_i$  # 上下标在正上、正下

${\sum }_{i=1}^n{x}_i$

$\sum _{i=1}^n{x}_i$

注意：这里是把 \sum 写到了$$里才有了第二种强制将上下标居于正上、正下的写法。
如果 \sum 不写在$$里，则直接写

\sum_{i=1}^{n}x_i

也会显示成正上、正下的效果。
同理，如果\sum 不写在$$里的时候我们又希望上下标是显示在右边（反复横跳(ˉ▽ˉ；)...），则加上\nolimits

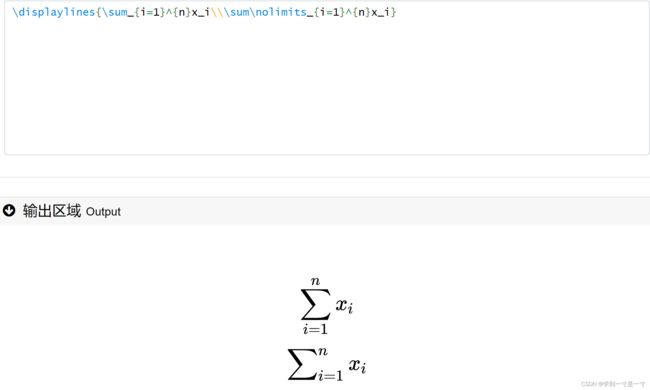
求和符号的上下标位置也可以缺省

$\sum\limits_i \sum\limits^n$

$\sum _i\sum ^n$

数组矩阵

下面把矩阵的几种写法写在一起，方便比较记忆

% 无括号矩阵
\begin{matrix}
-1 & 1 & 2\\
0 & 1 & 4\\
\end{matrix}
% 圆括号矩阵
\begin{pmatrix}
-1 & 1 & 2\\
0 & 1 & 4\\
\end{pmatrix}
% 单竖线矩阵
\begin{vmatrix}
-1 & 1 & 2\\
0 & 1 & 4\\
\end{vmatrix}
% 双竖线矩阵
\begin{Vmatrix}
-1 & 1 & 2\\
0 & 1 & 4\\
\end{Vmatrix}
% 方括号矩阵
\begin{bmatrix}
-1 & 1 & 2\\
0 & 1 & 4\\
\end{bmatrix}
% 花括号矩阵
\begin{Bmatrix}
-1 & 1 & 2\\
0 & 1 & 4\\
\end{Bmatrix}

− 1 1 2 0 1 4 ( − 1 1 2 0 1 4 ) ∣ − 1 1 2 0 1 4 ∣ ∥ − 1 1 2 0 1 4 ∥ [ − 1 1 2 0 1 4 ] { − 1 1 2 0 1 4 } \begin{gathered} \begin{matrix} -1 & 1 & 2\\ 0 & 1 & 4\\ \end{matrix} \begin{pmatrix} -1 & 1 & 2\\ 0 & 1 & 4\\ \end{pmatrix} \begin{vmatrix} -1 & 1 & 2\\ 0 & 1 & 4\\ \end{vmatrix} \begin{Vmatrix} -1 & 1 & 2\\ 0 & 1 & 4\\ \end{Vmatrix} \begin{bmatrix} -1 & 1 & 2\\ 0 & 1 & 4\\ \end{bmatrix} \begin{Bmatrix} -1 & 1 & 2\\ 0 & 1 & 4\\ \end{Bmatrix} \end{gathered} −10​11​24​(−10​11​24​) ​−10​11​24​ ​ ​−10​11​24​ ​[−10​11​24​]{−10​11​24​}​

符号

属于

\in

$\in$

集合之间的各种关系（包含于、包含、真包含于……）

A\subset B
A\supset B
A\subseteq B
A\supseteq B
A\cap B
A\cup B
% A减B
A\setminus B
\emptyset

$$\begin{gathered} A\subset B \\ A\supset B \\ A\subseteq B \\ A\supseteq B \\ A\cap B \\ A\cup B \\ A\setminus B \\ \varnothing \end{gathered}$$

任意

\forall

$\forall$

存在

\exist或者\exists

$\exists$

因为、所以

\because 和 \therefore

$\because 和\therefore$

如果没有编译成功，需要在导言区导入宏包amssymb：

\usepackage{amssymb}

无穷大

\infty +\infty -\infty

$\infty 、+\infty 、-\infty$

尖括号（也就是常见的向量夹角$cos⟨a,b⟩$）

注意与小于号<，大于号> 区别

\langle

$⟨$

\rangle

$⟩$

小于等于、大于等于、不等于、恒等于、恒不等于

巧记：等于equation，所以这几个符号都是从 eq 词根出发的

\le 或者 \leq

$\le$

\ge 或者 \geq

$\ge$

\ne 或者 \neq

$\ne$

\equiv

$\equiv$

\not\equiv  # 注意这里只能是拼接\not和\equiv，\nequiv无效

$\not\equiv$

远小于、远大于

\ll，\gg

$\ll ，\gg$

约等于

\approx

$\approx$

向上取整、向下取整

\lceil x \rceil

$\lceil x\rceil$

\lfloor x \rfloor

$\lfloor x\rfloor$

绝对值

\left|-2\right| 或者 \vert -2\vert 或者  \lvert -2\rvert 

可以观察一下区别

$\left|-2\right|、|-2|、|-2|$

双竖线

\| A\| 或者 \left\|A\right\| 或者 \Vert A\Vert

$\Vert A\Vert 、\Vert A\Vert 、\Vert A\Vert$

花括号

\{ A\} 或者 \left\{ A \right\} 

$\{A\}、\left\{A\right\}$

乘号

\times 或者 ×

$\times 、\times$

开n次方

\sqrt{2}、\sqrt[4]{16}

$\sqrt{2}、\sqrt[4]{16}$

导数

% 求导
\frac{\mathrm{d}y}{\mathrm{d}x}
% 高阶导
\frac{\mathrm{d}^{n} y}{\mathrm{d}x^{n}}
% 求偏导
\frac{\partial{Loss}}{\partial{w}}
% 二阶偏导
\frac{\partial^{2}z}{\partial{x}^{2}}
\frac{\partial^{2}z}{\partial{x}\partial{y}}

$$\begin{gathered} \frac{\mathrm{d}y}{\mathrm{d}x}、\frac{{\mathrm{d}}^{n}y}{\mathrm{d}{x}^n} \\ \frac{\partial Loss}{\partial w}、\frac{{\partial }^{2}z}{\partial x^2}、\frac{{\partial }^{2}z}{\partial x\partial y} \end{gathered}$$

---

不断学习，持续更新……