回朔法之装载问题
装载问题描述:
有一批n个集装箱要装上2艘载重量分别为c1和c2的轮船,其中集装箱i的重量为Wi,且满足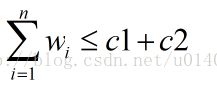
装载问题要求确定,是否有一个合理的装载方案可将这n个集装箱装上这2艘轮船,如果有,找出一种装载方案。(事实上,肯定有的啊)
策略:
<1>首先将第一艘轮船尽可能装满;
<2>然后将剩余的集装箱装上第二艘轮船
*回朔法解问题
*1.先明确定义问题的解空间,
*例如在下面的问题中解空间(0,0,0) (0,0,1) (0,1,0) (0,1,1) (1,0,0) (1,0,1) (1,1,0) (1,1,1)
*2.然后将解空间组织起来,装载问题这里用的是子集树,当然还有图
*3.深度优先搜索,配合剪枝函数
#include
using namespace std;
template
class Loading
{
friend Type MaxLoading(Type w[],Type c, int n,int bestx[]);
private:
void BackTrack(int i);
int n, //集装箱数
*x, //current result
*bestx; //current excellent result
Type *w, //集装箱重量数组
c, //第一艘轮船的载重量
cw, //当前载重量
bestw, //当前最优载重量
r; //the leaving weight
};
/*
*递归和回朔法在时间复杂赋仍为O(n2^n),但是迭代法省去了O(n)的递归栈空间
*
*
*/
template
void Loading::BackTrack(int i)
{
if(i>n-1) //reach the leaf of node ,n-1 is the array's index of objects because array is from 0 to n
{
if(cw>bestw)
{
for(int j=0;j// 当在i节点后面解空间找到最优解或者无最优解时,都得进行回朔,判断除掉i时,是否也存在最优解(cw+r>bestw)
//剪枝函数也就在此时起到作用
}
if(cw+r>bestw) // cut the branch
{
x[i]=0;
BackTrack(i+1); //x[i]=0
}
r+=w[i];
}
template
Type MaxLoading(Type w[],Type c,int n,int bestx[])
{
Loading X;
//init x object
X.x=new int[n]; //used to the temp array
X.w=w;
X.c=c;
X.n=n;
X.bestx=bestx;
X.bestw=0;
X.cw=0;
//init r
X.r=0;
for(int i=0;i
Type MaxLoading(Type w[],Type c,int n,int bestx[])
{
//itration fuction
int i=0;
int *x=new int[n];
Type bestw=0,cw=0,r=0;
for(int j=0;j=c
{
r-=w[i];
cw+=w[i];
x[i]=1;
i++;
}
if(i>n-1) //if the node has reached the bottom, and updating the bestw
{
for(int j=0;j0&&!x[i]) //when x[i] is 0,show the son tree is right son tree
{
r+=w[i];
i--;
}
if(i==0)
{
delete[] x;
return bestw;
}
x[i]=0; //enter the right son tree relative to the father node but not root node
cw-=w[i];
i++;
}
}
}
//even thought adding the fuction of cutting the branch,the complex of time is still O(2^n),O() represents the bad situation.
int main()
{
int w[3]={10,40,40};
int c=50;
int n=3;
int bestx[3];
int ExcWeight=MaxLoading(w,c,n,bestx); //guaruateeing the value is lower or equal to 50
cout<<"the excellent weight is "<