数据结构-队列(Queue)
队列(Queue)
队列的基本概念
定义
队列(Queue)。队列简称队。是一种操作受限的线性表,只允许在表的一端进行插入,而在表的另一端进行删除。向队列中插入元素称为入队或进队;删除元素称为出队或离队。其操作特性为先进先出(First In First Out,FIFO),并且只允许在队尾进,队头出。
![]()
队头(Front):允许删除的一端,又称队首
队尾(Rear):允许插入的一端
空队列:不包含任何元素的空表
队列的基本操作
1)InitQueue(&Q):初始化队列,构造一个空队列Q
2)QueueEmpty(Q):判断一个队列是否为空
3)EnQueue(&Q,x):入队,若队列未满,则将x加入使之成为新队尾
4)DeQueue(&Q,&x):出队,若队列非空,则将队首元素删除,并用x返回
5)GetHead(Q,&x):读队头元素,若栈顶元素非空,则用x返回栈顶元素
队列的顺序存储结构
队列的顺序存储
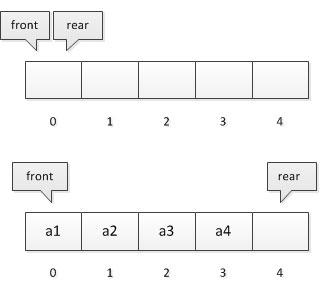
队列的顺序实现市值分配一块连续的存储单元存放队列中的元素,并附设两个指针 front 和 rear 分别指示队头元素和队尾元素的位置。设队头指针指向队头元素,队尾指针指向队尾元素的下一个位置。
队列的顺序存储类型可描述为:
#define MAXSIZE 100
typedef struct {
ElemType data[MAXSIZE];
int front,rear;
} SqQueue;
初始状态(队空):Q.front == Q.rear == 0;
进队操作:队不满时,先送值到队尾元素,将队尾指针加1
出队操作:队非空时,先删除队头元素,再将队头指针加1
由上可知,Q.front == Q.rear == 0 可以作为队列的判空条件,但能否能用 Q.rear == MAXSIZE 作为队列已满的条件呢?显然是不行的,因为队尾指针可能已经到了最尾端,但是队头指针可能不在初始位置,而是在队列的中间,这时入队出现“上溢”,但这种溢出并不是真正的溢出,data数组中仍存在可以放置元素的位置,所以为“假溢出”。
循环队列
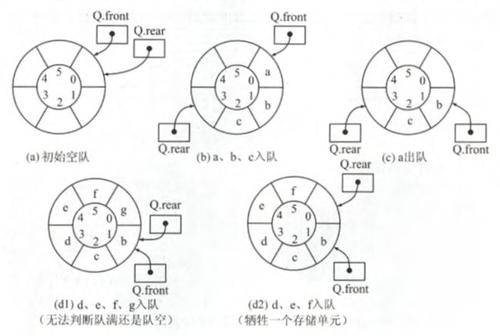
前面指出了队列的缺点,这里就引出循环队列的概念。将队列臆造成一个环状的空间,即把存储队列元素的表从按逻辑上视为一个环,称为循环队列。当队首指针 Q.front == MAXSIZE - 1,再前景一个位置就自动到0,这可以利用除法取余运算(%) 来实现。
初始化时:Q.front = Q.rear = 0;
队首指针进1:Q.front = (Q.front + 1) % MAXSIZE;
队尾指针进1:Q.rear = (Q.rear + 1)% MAXSIZE;
队列长度:(Q.front + MAXSIZE - Q.rear) % MAXSIZE;
循环队列如何判断队满还是队空?
1)一般的做法是:入队时少入对一个队列单元,约定“队尾指针的下一个标志是队头指针 作为 队满的标志“:
队空条件:Q.front == Q.rear
队满条件:(Q.rear + 1) % MAXSIZE == Q.front
队列长度:(Q.rear - Q.front + MAXSIZE )% MAXSIZE
2)在类型中添加表示成员个数的数据成员。队空时 Q.size == 0;队满时 Q.size == MAXSIZE
3)类型中添加tag 数据成员,以区分是队满还是对空。tag ==0 ,若因删除导致Q.front == Q.rear ,则为队空;若tag == 1,若因添加导致Q.front == Q.rear,则为队满。
循环队列的操作
1、初始化
void InitQueue(SqQueue& Q){
Q.front = Q.rear = 0;
}
2、判队空
bool QueueEmpty(SqQueue Q){
if( Q.front == Q.rear){
return true;
}
return false;
}
3、入队
bool EnQueue(SqQueue& Q, ElemType x){
if( (Q.rear + 1) % MAXSIZE == Q.front ){
return false;
}
Q.data[Q.rear] = x;
Q.rear = ( Q.rear + 1) % MAXSIZE;//队尾指针加1取模,这步操作很容易写错
return true;
}
4、出队
bool DeQueue(SqQueue& Q, ElemType &x){
if( Q.rear == Q.front ){
return false;
}
x = Q.data[Q.front];
Q.front = (Q.front + 1) % MAXSIZE;//队头指针加1取模
return true;
}
队列的链式存储结构
队列的链式存储
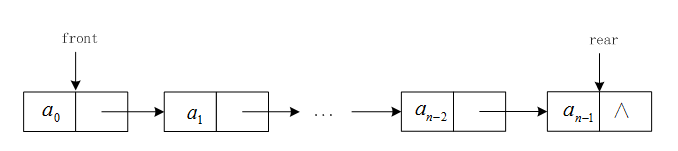
队列的链式存储又称为 链队列,它实际上是一个同时带有一个队头指针和队尾指针的单链表。头指针指向队头结点,尾指针指向最后一个结点。
不带头结点的链式队列
队列的链式存储类型可描述为:
typedef struct LinkNode{
ElemType data;
struct LinkNode* next;
}LinkNode;
typedef struct{
LinkNode *front, *rear;
}LinkQueue;
当Q.front == nullptr 且 Q.rear == nullptr 时,链式队列为空。
出队时,若不空,则将队头元素删除,Q.front 指向下一个结点;入队时,新建一个结点,将新结点插入到链队列的尾端,并让Q.rear指向这个新插入的结点。
不带头结点的链式队列在操作上往往比较麻烦,因此通常将链式队列设计成一个带头结点的单链表,这样插入和删除就统一了。
链式队列的基本操作
1、初始化
void InitQueue(LinkQueue& Q){
//初始化时,Q.front 和 Q.rear 同时指向头结点
Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
Q.front->next = nullptr;
}
2、判队空
bool QueueEmpty(LinkQueue Q){
if( Q.front == Q.rear){
return true;
}
return false;
}
3、入队
bool EnQueue(LinkQueue& Q, ElemType x){
LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = x;
s->next = nullptr;
Q.rear->next = s;
Q.rear = s;
return true;
}
4、出队
bool DeQueue(LinkQueue& Q, ElemType &x){
if( Q.rear == Q.front ){
return false;
}
LinkNode* p = Q.front->next; //因为有头结点,所以队头节点为Q.front->next
x = p->data;
Q.front->next = p->next;
if( Q.rear == p ){ //只剩一个结点,删除后变空只剩头结点
Q.rear = Q.front;
}
free(p);
return true;
}
双端队列
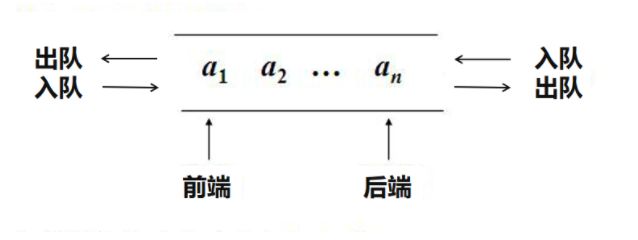
双端是允许两端都可以进行入队和出队操作的队列。逻辑结构仍然是线性结构,将队列的两端分别称为前端和后端,连段都可以入队和出队。
在双端队列进队时,前端进的元素排列在队列中后端进的元素的前面,后端进的元素排在前端进的元素的后面。在双端队列中,无论是前端还是后段,先出去的元素排列在后出去的元素前面。
输出受限的双端队列:有一端不能进行删除,这样的双端队列叫做 输出受限的双端队列。
输入受限的双端队列:有一端不能进行插入,这样的双端队列叫做 输出受限的双端队列。
如果觉得本文对你有帮助的话,不妨关注作者一波,小小的关注其实对我很重要。更多高质量内容与资料请访问:数据结构简单学,个人主页:修心的小屋
如果喜欢的话,不妨关注一波,谢谢啦。
![]()