数据在计算机中的表示:原码 反码 补码 移码
文章目录
- 一.原码
-
- 1.正整数原码
- 2.负整数原码
- 二.补码
-
- 1.整数的补码
- 2.定点小数的补码
- ==⭐补码的性质⭐==
- 三.反码
- 四.移码
- 例题与思考
一.原码
原码是有符号定点数
有符号数:n位二进制的有符号数中,最高位表示符号位,0表示正数,1表示负数,其余n-1位表示数值位,其可表示的范围为:-127~+127
1.正整数原码
正数的原码就是其本身,即有符号正数的二进制形式,例如5的八位原码为:00000101.
正数原码可表示的范围为
0 — + ( 2 n − 1 − 1 ) 0 \space— \space+(2^{n-1}-1) 0 — +(2n−1−1)
例如8位正数原码的范围为0~127:00000000-01111111
2.负整数原码
负数的原码是最高位取1,其余n-1位表示为负数的绝对值。
以8位原码为例,-12的原码为:10001100
负数原码可表示的范围为
− 0 — − ( 2 n − 1 − 1 ) -0\space—-(2^{n-1}-1) −0 —−(2n−1−1)
例如8位负数原码的范围为-0~-127:10000000-11111111
二.补码
在介绍补码概念之前,先介绍一下“模”的概念:“模”是指一个计量系统的计数范围,如过去计量粮食用的斗、时钟等。计算机也可以看成一个计量机器,因为计算机的字长是定长的,即存储和处理的位数是有限的,因此它也有一个计量范围,即都存在一个“模”。如:时钟的计量范围是0~11,模=12。表示n位的计算机计量范围是,模=2^n,“模”实质上是计量器产生“溢出”的量,它的值在计量器上表示不出来,计量器上只能表示出模的余数。任何有模的计量器,均可化减法为加法运算————百度百科
补码运算的理解:
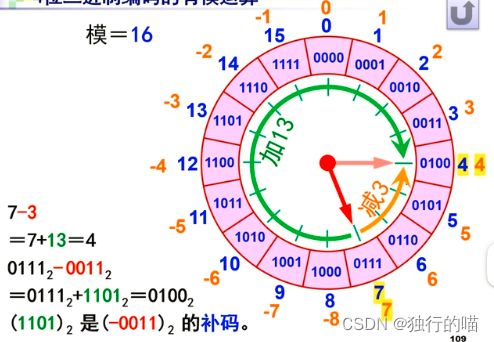
用一个类似于钟表布局的图来解释补码的运算:
从图中我们可以看到,假如我们要做7-3的运算,那么有两种方法可以实现:
- 直接让7-3,即逆时针转动三个数
- 让7+13,即顺时针转动13个数也能达到与减3同样的效果
在计算机运算电路的设计中,我们希望通过把减法转换成加法而用加法电路来替代减法电路的功能,以达到简化硬件设计的目的。
那么从上面的例子中,在模16的运算中我们显然可以通过+13的方式来替代-3的方式来实现相同的运算结果。即本质就是,对于一个数正x,加上:(模-x)的原码 等价于 减去:x的原码。通过这一点,我们对于一个负数x,加上x也就等价于加上(模-|x|)的原码 。
而对于加上的这个改变之后的原码,我们单独称其为补码。
上面例子7-3的运算中,可见3的原码是0011,而-3的操作等价于+(-3),即+ [ − 3 ] 补 [-3]_补 [−3]补,-3的补码即为16-3=13的原码:1101。
经验算:7的原码+13的原码=0111+1101=0100(舍弃最高位)
而0100确实是4的原码,如此一来我们就将对原码的减法转换为了对补码的加法。
下面我们对补码做出具体的规定:
1.整数的补码
求整数补码的方法:
1.若是正整数,则其补码与原码相同
2.若是负整数,则需要通过以下两个步骤获得补码:
- 1)符号位不变,其余位取反
- 2)最低位+1
例如求取15和-23的补码(8位):
15的原码为:00001111
15的补码位:00001111
-23的原码为:10010111
-23的补码为:11101001
更简便的做法是:从左往右数第一个1以及1右边的数不变,左边的数除符号位外取反
整数补码表示的范围:
n位整数补码可表示的真值范围为:
− 2 n − 1 — 2 n − 1 − 1 -2^{n-1}—2^{n-1}-1 −2n−1—2n−1−1
其中10000·····000表示-2^(n-1),例如8位补码中10000000表示-128
2.定点小数的补码
若小数用n位二进制数表示,则小数补码的定义为:
[ X ] 补 = { X 1 > X ≥ 0 X + 2 0 > X ≥ − 1 [X]_补=\left\{ \begin{aligned} &X &&1>X\ge0 \\ &X+2 && 0>X\ge-1\\ \end{aligned} \right. [X]补={XX+21>X≥00>X≥−1
n位补码可表示的定点小数的范围为:
− 1 → + ( 1 − 2 − n + 1 ) \space -1\to+(1-2^{-n+1}) −1→+(1−2−n+1)
注意:
- 1.1111…1111111(n个1)表示 − 2 − n + 1 -2^{-n+1} −2−n+1的补码
- 1.000…0000000(n-1个0)表示-1的补码(定点小数),而在定点整数中,-1的补码为:1111111111111(n个1)
- 证明:按照定点小数的定义 [ − 1 ] 补 = [ − 1 + 2 ] 无 符 号 小 数 = 1.0000000 [-1]_补=[-1+2]_{无符号小数}=1.0000000 [−1]补=[−1+2]无符号小数=1.0000000
⭐补码的性质⭐
- (1)性质1:正数的补码是其本身
- (2)性质2:对补码再次求补,得到其原码
- (3)性质3: [ x + y ] 补 = [ x ] 补 + [ y ] 补 [x+y]_补 = [x]_补+[y]_补 [x+y]补=[x]补+[y]补
- (4)性质4: [ x ] 补 = [ 模 + x ] 码 值 [x]_补=[模+x]_{码值} [x]补=[模+x]码值
- (5)性质5:若x > y(x,y同号),则 [ x ] 补 > [ y ] 补 [x]_补>[y]_补 [x]补>[y]补
证:若x,y>0,易证;若x,y<0, [ x ] 补 = [ 模 + x ] 码 值 , [ y ] 补 = [ 模 + y ] 码 值 , x > y , 故 [ x ] 补 > [ y ] 补 [x]_补=[模+x]_{码值},[y]_补=[模+y]_{码值},x>y,故[x]_补>[y]_补 [x]补=[模+x]码值,[y]补=[模+y]码值,x>y,故[x]补>[y]补 - (6)性质6: 若 [ x ] 补 = 符 号 位 x 0 x 1 x 2 x 3 x 4 . . . . x n , 则 [ 2 n x ] 补 若[x]_补=符号位x_0x_1x_2x_3x_4....xn,则[2^nx]_补 若[x]补=符号位x0x1x2x3x4....xn,则[2nx]补为符号位不变,将其余位左移n位,溢出位舍去。
三.反码
正数的反码与原码相同
负数的反码为:符号位不变,其余位取反
四.移码
移码多用于浮点数中表示阶码,均为正数
正数移码的定义为:
[ x ] 移 = 2 n − 1 + X 真 值 ( 2 n − 1 > X ≥ − 2 n − 1 ) m o d ( 2 n ) [x]_{移}=2^{n-1}+X_{真值} (2^{n-1}>X\ge-2^{n-1}) mod(2^n) [x]移=2n−1+X真值(2n−1>X≥−2n−1)mod(2n)
移码与补码的关系:移码为补码的符号位取反
移码的特点:移码的大小反映了数值X的大小,即若 [ X ] 移 > [ Y ] 移 , 则 X 真 值 > Y 真 值 [X]_移>[Y]_{移},则X_{真值}>Y_{真值} [X]移>[Y]移,则X真值>Y真值 反过来亦成立。
例题与思考
1.设X为小数,X在什么范围内,有 [ X ] 补 > [ X ] 原 [X]_补>[X]_原 [X]补>[X]原
分析:当X>0时,显然: [ X ] 补 = [ X ] 原 [X]_补=[X]_原 [X]补=[X]原
\space \space\space \space\space\space\space\space\space 当X<0时, [ X ] 补 = [ X 真 值 + 2 ( m o d ) ] 码 值 ; [ X ] 原 码 = [ 1 − X 真 值 ] 码 值 [X]_补=[X_{真值}+2(mod)]_{码值};[X]_{原码}=[1-X_{真值}]_{码值} [X]补=[X真值+2(mod)]码值;[X]原码=[1−X真值]码值
注:该码值所指的是当成一般无符号定点小数 的值
解析:若求: [ X ] 补 > [ X ] 原 [X]_补>[X]_原 [X]补>[X]原,即求 [ X 真 值 + 2 ( m o d ) ] 码 值 > [ 1 − X 真 值 ] 码 值 [X_{真值}+2(mod)]_{码值}>[1-X_{真值}]_{码值} [X真值+2(mod)]码值>[1−X真值]码值
即X+2>1-X, 解不等式得:X>-1/2
2.(西电15年833真题节选)假设机器字长为8位,已知[X]补=5AH,[Y]补=B6H,求:
(1)[2X]补;(2)[2Y]补;(3)[X/2]补;(4)[Y/4]补 ;
(采用截断法舍入)
分析:8位补码所能表示的真值范围显然问:-128到127(判断溢出)
将 5AH展开成8位2进制:0101 1010(补) = +80(真值)
将 B6H展开为8位2进制:1011 0110 (补)= 1100 1010(原)= -74(真值)
-
(1)[2X]补:
2X真值为:160,显然溢出
采用上文所列出的补码性质(6)将X的补码数值部分左移1为得:0011 0100 = 3 4 H -
(2)[2Y]补:
2Y真值为-148,显然溢出,
将Y补码数值部分左移1位得:1110 1100 = E C H -
(3)[X/2]补:
X/2真值为40,未溢出
将X补码数值部分右移1位得:0010 1101 = 2 D H -
(4)[Y/4]补:
Y/4真值为18.5,未溢出
将Y补码数值部分右移2位得:1110 1101 = E D H