FGPA实现基于cordic算法的反正切函数
一、cordic原理(圆坐标系):
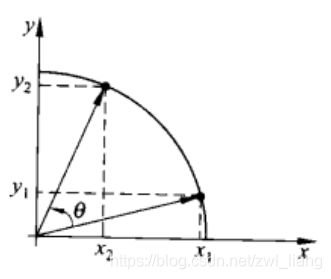
1、如图1所示,点 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)可以通过点 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)旋转来得到,根据givens旋转可以得到如下公式
x 2 = x 1 ∗ c o s θ − y 1 ∗ s i n θ x_2 = x_1*cos\theta-y_1*sin\theta x2=x1∗cosθ−y1∗sinθ
y 2 = x 1 ∗ s i n θ + y 1 ∗ c o s θ y_2 = x_1*sin\theta+y_1*cos\theta y2=x1∗sinθ+y1∗cosθ
2、上式提出 c o s θ 后 cos\theta后 cosθ后
x 2 = c o s θ ∗ ( x 1 − y 1 ∗ t a n θ ) x_2 = cos\theta*( x_1-y_1*tan\theta) x2=cosθ∗(x1−y1∗tanθ)
y 2 = c o s θ ∗ ( x 1 + y 1 ∗ t a n θ ) y_2 = cos\theta*( x_1+y_1*tan\theta) y2=cosθ∗(x1+y1∗tanθ)
3、去掉cos\theta后可得到伪旋转方程式如下
x 2 ∗ = x 1 − y 1 ∗ t a n θ x^*_2 = x_1-y_1*tan\theta x2∗=x1−y1∗tanθ
y 2 ∗ = x 1 + y 1 ∗ t a n θ y^*_2 = x_1+y_1*tan\theta y2∗=x1+y1∗tanθ
伪旋转后,x与y的值都相比实际值增加了 c o s − 1 θ cos^{-1}\theta cos−1θ,且 c o s − 1 θ cos^{-1}\theta cos−1θ>1。

伪旋转的主要作用是得到只含正切三角函数的等式,正切三角函数可以使其用 2 − i 2^{-i} 2−i来表示,即令 t a n θ = 2 − i tan\theta=2^{-i} tanθ=2−i。此时伪旋转公式可以变为如下形式
x 2 ∗ = x 1 − y 1 ∗ 2 − i x^*_2 = x_1-y_1*2^{-i} x2∗=x1−y1∗2−i
y 2 ∗ = x 1 + y 1 ∗ 2 − i y^*_2 = x_1+y_1*2^{-i} y2∗=x1+y1∗2−i
这样使得对任意角度的旋转变成了通过一些小角度的旋转i次来完成的,也迭代了i次,适合硬件电路的实现,下表是迭代13次后各次迭代的 θ , c o s , t a n \theta, cos,tan θ,cos,tan函数值

如上表所示,此方法支持的角度范围为(-99.7,99.7),二三象限的角度值可以通过三角函数的恒等变换来转化到此范围内,再进行计算。
4、此时的伪旋转公式可以改为如下迭代公式
x ( i + 1 ) = x ( i ) − d i ( 2 − i y ( i ) ) x^{(i+1)}=x^{(i)}-d_i(2^{-i}y^{(i)}) x(i+1)=x(i)−di(2−iy(i))
y ( i + 1 ) = y ( i ) + d i ( 2 − i x ( i ) ) y^{(i+1)}=y^{(i)}+d_i(2^{-i}x^{(i)}) y(i+1)=y(i)+di(2−ix(i))
同时设置一个角度累加方程,来记录角度的累加值
z ( i + 1 ) = z ( i ) − d i ∗ t h e t a ( i ) z^{(i+1)}=z^{(i)}-d_i*theta^{(i)} z(i+1)=z(i)−di∗theta(i)
注: d i d_i di的值为1或者-1,主要是用来确定旋转的方向,例如要计算sin30,当 z ( i + 1 ) z^{(i+1)} z(i+1)>30时减少角度,小于30则加大角度
5、令伸缩因子 k n = c o s 45 ∗ c o s 26.5 ∗ c o s 14.03 ∗ . . . ∗ c o s 0.0139 = 0.60725941 k_n=cos45*cos26.5*cos14.03*...*cos0.0139=0.60725941 kn=cos45∗cos26.5∗cos14.03∗...∗cos0.0139=0.60725941
二、操作模式
1、操作模式有两种,分别为旋转操作模式和向量操作模式,不同的模式中的 d i d_i di定义不同。在旋转模式中 d i = s i g n ( z ( i ) ) d_i=sign(z^{(i)}) di=sign(z(i)),在向量模式中 d i = − s i g n ( x ( i ) y ( i ) ) d_i=-sign(x^{(i)}y^{(i)}) di=−sign(x(i)y(i))
2、旋转模式下n次迭代后的公式如下
x ( n ) = k n ( x ( 0 ) c o s z ( 0 ) − y ( 0 ) s i n z ( 0 ) ) x^{(n)}=k_n(x^{(0)}cosz^{(0)}-y^{(0)}sinz^{(0)}) x(n)=kn(x(0)cosz(0)−y(0)sinz(0))
y ( n ) = k n ( y ( 0 ) c o s z ( 0 ) + x ( 0 ) s i n z ( 0 ) ) y^{(n)}=k_n(y^{(0)}cosz^{(0)}+x^{(0)}sinz^{(0)}) y(n)=kn(y(0)cosz(0)+x(0)sinz(0))
令 x ( 0 ) = 1 / k n , y ( 0 ) = 0 x^{(0)}=1/k_n,y^{(0)}=0 x(0)=1/kn,y(0)=0时,通过迭代使 z ( 0 ) z^{(0)} z(0)趋近0,就可以求得 c o s z ( 0 ) 与 s i n z ( 0 ) cosz^{(0)}与sinz^{(0)} cosz(0)与sinz(0)的值
例子: 当 z ( 0 ) = 30 z^{(0)}=30 z(0)=30时, c o s z ( 0 ) 与 s i n z ( 0 ) cosz^{(0)}与sinz^{(0)} cosz(0)与sinz(0)的求解如下表
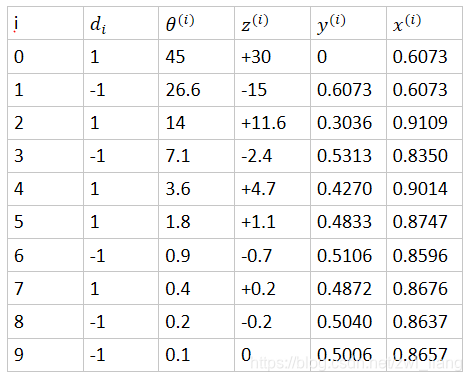
通过上表可知 s i n ( 3 0 o ) = y ( 9 ) = 0.5006 , c o s ( 3 0 o ) = x ( 9 ) = 0.8657 sin(30^o)=y^{(9)}=0.5006,cos(30^o)=x^{(9)}=0.8657 sin(30o)=y(9)=0.5006,cos(30o)=x(9)=0.8657
3、向量模式下n次迭代后的公式如下
x ( n ) = k n x ( 0 ) 2 + y ( 0 ) 2 x^{(n)}=k_n\sqrt {x^{(0)^2}+y^{(0)^2}} x(n)=knx(0)2+y(0)2
y ( n ) = 0 y^{(n)}=0 y(n)=0
z ( n ) = z ( 0 ) + t a n − 1 ( y ( 0 ) x ( 0 ) ) z^{(n)}=z^{(0)}+tan^{-1}(\frac{y^{(0)}}{x^{(0)}}) z(n)=z(0)+tan−1(x(0)y(0))
令 z ( 0 ) z^{(0)} z(0)=0时,可以得到反正切值 t a n − 1 ( y ( 0 ) x ( 0 ) ) tan^{-1}(\frac{y^{(0)}}{x^{(0)}}) tan−1(x(0)y(0))
例子: 令 y ( 0 ) = 2 , x ( 0 ) = 1 y^{(0)}=2,x^{(0)}=1 y(0)=2,x(0)=1时, t a n − 1 ( y ( 0 ) x ( 0 ) ) tan^{-1}(\frac{y^{(0)}}{x^{(0)}}) tan−1(x(0)y(0))的值
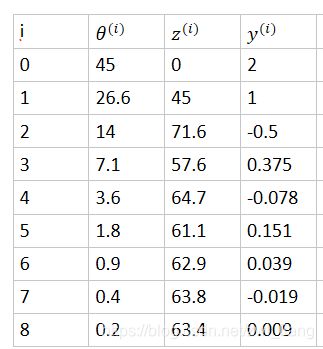
上式 z ( 8 ) z^{(8)} z(8)=63.4为最终结果
三、FPGA实现反正切函数
这次实现用了16次的迭代,为了方便计算代码中的数值扩大了65536倍,最后输出在缩小16倍
下面是相应的代码。
**反正切函数verilog代码**
/***********Filename ﹕Cordic_atan .v**************
************Author ﹕Wenliang Zhou*********
************Description ﹕Implementation of arctangent function based on CORDIC**********
************Called by ﹕DUT**********
************Revision time﹕2019.11.26**********
************Revision ﹕2.0**********
************Email ﹕[email protected]**********
***********/
module Cordic_atan
(
clk_50M,rst_n,
x,
y,
start,
finished,
atan
);
input clk_50M;
input rst_n;
input [31:0] x;
input [31:0] y;
input start;
output finished;
output [31:0] atan;
`define angle_0 32'd2949120 //45°*2^16
`define angle_1 32'd1740992 //26.5651°*2^16
`define angle_2 32'd919872 //14.0362°*2^16
`define angle_3 32'd466944 //7.1250°*2^16
`define angle_4 32'd234368 //3.5763°*2^16
`define angle_5 32'd117312 //1.7899°*2^16
`define angle_6 32'd58688 //0.8952°*2^16
`define angle_7 32'd29312 //0.4476°*2^16
`define angle_8 32'd14656 //0.2238°*2^16
`define angle_9 32'd7360 //0.1119°*2^16
`define angle_10 32'd3648 //0.0560°*2^16
`define angle_11 32'd1856 //0.0280°*2^16
`define angle_12 32'd896 //0.0140°*2^16
`define angle_13 32'd448 //0.0070°*2^16
`define angle_14 32'd256 //0.0035°*2^16
`define angle_15 32'd128 //0.0018°*2^16
parameter Pipeline = 16;
parameter K = 32'h09b74; //K=0.607253*2^16,32'h09b74,
reg signed [31:0] atan;
reg signed [31:0] x0=0,y0=0,z0=0;
reg signed [31:0] x1=0,y1=0,z1=0;
reg signed [31:0] x2=0,y2=0,z2=0;
reg signed [31:0] x3=0,y3=0,z3=0;
reg signed [31:0] x4=0,y4=0,z4=0;
reg signed [31:0] x5=0,y5=0,z5=0;
reg signed [31:0] x6=0,y6=0,z6=0;
reg signed [31:0] x7=0,y7=0,z7=0;
reg signed [31:0] x8=0,y8=0,z8=0;
reg signed [31:0] x9=0,y9=0,z9=0;
reg signed [31:0] x10=0,y10=0,z10=0;
reg signed [31:0] x11=0,y11=0,z11=0;
reg signed [31:0] x12=0,y12=0,z12=0;
reg signed [31:0] x13=0,y13=0,z13=0;
reg signed [31:0] x14=0,y14=0,z14=0;
reg signed [31:0] x15=0,y15=0,z15=0;
reg signed [31:0] x16=0,y16=0,z16=0;
reg [4:0] count;
always@ (posedge clk_50M or negedge rst_n) begin
if(!rst_n)
count <= 4'b00;
else if( start ) begin
if( count!=5'd18 )
count <= count+1'b1;
else if( count == 5'd18 )
count <= 0;
end
else
count <= 5'h00;
end
assign finished = (count == 5'd18)?1'b1:1'b0;
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x0 <= 1'b0;
y0 <= 1'b0;
z0 <= 1'b0;
end
else
begin
x0 <= x;
y0 <= y;
z0 <= 0;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x1 <= 1'b0;
y1 <= 1'b0;
z1 <= 1'b0;
end
else if(x0[31] == y0[31])//Di is -1;
begin
x1 <= x0 + y0;
y1 <= y0 - x0;
z1 <= z0 + `angle_0;
end
else
begin //Di is 1;
x1 <= x0 - y0;
y1 <= y0 + x0;
z1 <= z0 - `angle_0;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x2 <= 1'b0;
y2 <= 1'b0;
z2 <= 1'b0;
end
else if(x1[31] == y1[31])
begin
x2 <= x1 + (y1 >>> 1);
y2 <= y1 - (x1 >>> 1);
z2 <= z1 + `angle_1;
end
else
begin
x2 <= x1 - (y1 >>> 1);
y2 <= y1 + (x1 >>> 1);
z2 <= z1 - `angle_1;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x3 <= 1'b0;
y3 <= 1'b0;
z3 <= 1'b0;
end
else if(x2[31] == y2[31])
begin
x3 <= x2 + (y2 >>> 2);
y3 <= y2 - (x2 >>> 2);
z3 <= z2 + `angle_2;
end
else
begin
x3 <= x2 - (y2 >>> 2);
y3 <= y2 + (x2 >>> 2);
z3 <= z2 - `angle_2;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x4 <= 1'b0;
y4 <= 1'b0;
z4 <= 1'b0;
end
else if(x3[31] == y3[31])
begin
x4 <= x3 + (y3 >>> 3);
y4 <= y3 - (x3 >>> 3);
z4 <= z3 + `angle_3;
end
else
begin
x4 <= x3 - (y3 >>> 3);
y4 <= y3 + (x3 >>> 3);
z4 <= z3 - `angle_3;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x5 <= 1'b0;
y5 <= 1'b0;
z5 <= 1'b0;
end
else if(x4[31] == y4[31])
begin
x5 <= x4 + (y4 >>> 4);
y5 <= y4 - (x4 >>> 4);
z5 <= z4 + `angle_4;
end
else
begin
x5 <= x4 - (y4 >>> 4);
y5 <= y4 + (x4 >>> 4);
z5 <= z4 - `angle_4;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x6 <= 1'b0;
y6 <= 1'b0;
z6 <= 1'b0;
end
else if(x5[31] == y5[31])
begin
x6 <= x5 + (y5 >>> 5);
y6 <= y5 - (x5 >>> 5);
z6 <= z5 + `angle_5;
end
else
begin
x6 <= x5 - (y5 >>> 5);
y6 <= y5 + (x5 >>> 5);
z6 <= z5 - `angle_5;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x7 <= 1'b0;
y7 <= 1'b0;
z7 <= 1'b0;
end
else if(x6[31] == y6[31])
begin
x7 <= x6 + (y6 >>> 6);
y7 <= y6 - (x6 >>> 6);
z7 <= z6 + `angle_6;
end
else
begin
x7 <= x6 - (y6 >>> 6);
y7 <= y6 + (x6 >>> 6);
z7 <= z6 - `angle_6;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x8 <= 1'b0;
y8 <= 1'b0;
z8 <= 1'b0;
end
else if(x7[31] == y7[31])
begin
x8 <= x7 + (y7 >>> 7);
y8 <= y7 - (x7 >>> 7);
z8 <= z7 + `angle_7;
end
else
begin
x8 <= x7 - (y7 >>> 7);
y8 <= y7 + (x7 >>> 7);
z8 <= z7 - `angle_7;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x9 <= 1'b0;
y9 <= 1'b0;
z9 <= 1'b0;
end
else if(x8[31] == y8[31])
begin
x9 <= x8 + (y8 >>> 8);
y9 <= y8 - (x8 >>> 8);
z9 <= z8 + `angle_8;
end
else
begin
x9 <= x8 - (y8 >>> 8);
y9 <= y8 + (x8 >>> 8);
z9 <= z8 - `angle_8;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x10 <= 1'b0;
y10 <= 1'b0;
z10 <= 1'b0;
end
else if(x9[31] == y9[31])
begin
x10 <= x9 + (y9 >>> 9);
y10 <= y9 - (x9 >>> 9);
z10 <= z9 + `angle_9;
end
else
begin
x10 <= x9 - (y9 >>> 9);
y10 <= y9 + (x9 >>> 9);
z10 <= z9 - `angle_9;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x11 <= 1'b0;
y11 <= 1'b0;
z11 <= 1'b0;
end
else if(x1[31] == y10[31])
begin
x11 <= x10 + (y10 >>> 10);
y11 <= y10 - (x10 >>> 10);
z11 <= z10 + `angle_10;
end
else
begin
x11 <= x10 - (y10 >>> 10);
y11 <= y10 + (x10 >>> 10);
z11 <= z10 - `angle_10;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x12 <= 1'b0;
y12 <= 1'b0;
z12 <= 1'b0;
end
else if(x11[31] == y11[31])
begin
x12 <= x11 + (y11 >>> 11);
y12 <= y11 - (x11 >>> 11);
z12 <= z11 + `angle_11;
end
else
begin
x12 <= x11 - (y11 >>> 11);
y12 <= y11 + (x11 >>> 11);
z12 <= z11 - `angle_11;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x13 <= 1'b0;
y13 <= 1'b0;
z13 <= 1'b0;
end
else if(x12[31] == y12[31])
begin
x13 <= x12 + (y12 >>> 12);
y13 <= y12 - (x12 >>> 12);
z13 <= z12 + `angle_12;
end
else
begin
x13 <= x12 - (y12 >>> 12);
y13 <= y12 + (x12 >>> 12);
z13 <= z12 - `angle_12;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x14 <= 1'b0;
y14 <= 1'b0;
z14 <= 1'b0;
end
else if(x13[31] == y13[31])
begin
x14 <= x13 + (y13 >>> 13);
y14 <= y13 - (x13 >>> 13);
z14 <= z13 + `angle_13;
end
else
begin
x14 <= x13 - (y13 >>> 13);
y14 <= y13 + (x13 >>> 13);
z14 <= z13 - `angle_13;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x15 <= 1'b0;
y15 <= 1'b0;
z15 <= 1'b0;
end
else if(x14[31] == y14[31])
begin
x15 <= x14 + (y14 >>> 14);
y15 <= y14 - (x14 >>> 14);
z15 <= z14 + `angle_14;
end
else
begin
x15 <= x14 - (y14 >>> 14);
y15 <= y14 + (x14 >>> 14);
z15 <= z14 - `angle_14;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n)
begin
x16 <= 1'b0;
y16 <= 1'b0;
z16 <= 1'b0;
end
else if(x15[31] == y15[31])
begin
x16 <= x15 + (y15 >>> 15);
y16 <= y15 - (x15 >>> 15);
z16 <= z15 + `angle_15;
end
else
begin
x16 <= x15 - (y15 >>> 15);
y16 <= y15 + (x15 >>> 15);
z16 <= z15 - `angle_15;
end
end
always @ (posedge clk_50M or negedge rst_n)
begin
if(!rst_n) begin
atan <= 1'b0;
end
else if(finished)begin
atan <= z16>>16;
end
end
endmodule
**testbench代码**
/***********Filename ﹕Cordic_atan_tb .v**************
************Author ﹕Wenliang Zhou*********
************Description ﹕Testbench document of Cordic_atan**********
************Called by ﹕Testbench**********
************Revision time﹕2019.11.26**********
************Revision ﹕2.0**********
************Email ﹕[email protected]**********
***********/
`timescale 1 ns/1 ns
module cordic_atan_tb();
//时钟周期,单位为ns,可在此修改时钟周期。
parameter CYCLE = 20;
//复位时间,此时表示复位3个时钟周期的时间。
parameter RST_TIME = 3 ;
// Inputs
reg clk_50M;
reg rst_n;
reg [15:0] cnt;
reg [15:0] cnt_n;
reg start;
reg [31:0] x;
reg [31:0] y;
wire [31:0] Error;
wire [31:0] atan;
// Instantiate the Unit Under Test (UUT)
Cordic_atan uut(
.clk_50M (clk_50M ),
.rst_n (rst_n ),
.x (x ),
.y (y ),
.start (start ),
.finished (finished ),
.atan (atan )
);
//生成本地时钟50M
initial begin
clk_50M = 0;
forever
#(CYCLE/2)
clk_50M=~clk_50M;
end
//产生复位信号
initial begin
rst_n = 1;
#2;
rst_n = 0;
#(CYCLE*RST_TIME);
rst_n = 1;
end
//输入信号din0赋值方式
initial begin
#1;
//赋初值
x = 1;
y = 1;
start = 1;
end
endmodule
