主成分分析(PCA)及python原理实现
PCA定义:
该定义来自于秒懂百科:
PCA(principal components analysis)即主成分分析技术,又称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
在统计学中,主成分分析PCA是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。主成分分析经常用于减少数据集的维数,同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是,这也不是一定的,要视具体应用而定。
就是通过线性变换,将数据映射到低维的子空间中的降维方法,期间尽可能防止信息丢失。
数据降维:
降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。
即高维数据的低位表达,但必然会导致一部分信息的丢失。
维数灾难:
由于我们生活在并且习惯于3维世界,所以当我们尝试想象高维空间时,一般很难有个直观的感受。即使是一个4D的超立方体,在我们脑海中也很难进行想象,更不用说200-维的椭球体在1000-维空间的弯曲的样子了。下图是0D(0维)到4D超平面的一个示例:
降维的主要方法:
在我们深入了解特定降维算法之前,我们先看一下两个主要的降维方法:投影与流形学习。
投影:
投影指的是用一组光线将物体的形状投射到一个平面上去,称为“投影”。
在该平面上得到的图像,也称为“投影”。投影可分为正投影和斜投影。
正投影即是投射线的中心线垂直于投影的平面,其投射中心线不垂直于投射平面的称为斜投影。
一个是投影面,一个是映射面。
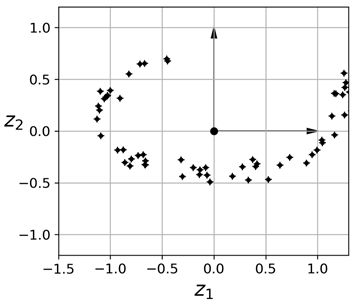
如果我们将3维所有训练实例垂直投影到这个2维子空间,则可以得到一个新的2维数据集,如下所示:
映射2维
数据从三维变到二维,数据线性变换,例如(x, y, z)垂直投影后就变成(x,y)。
需要注意的是,坐标轴对应的是两个新特征z1和z2(投影在这个平面上的坐标)。
不过,投影并不总是最好的降维方法。在很多情况下,子空间可能弯曲和旋转。
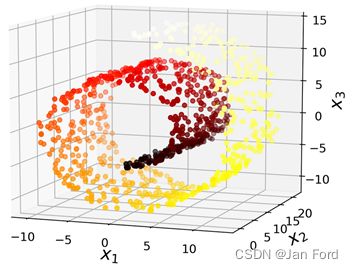
例如著名的瑞士卷数据集:
如果简单的将它们投影到一个平面(例如,直接丢弃x3)则会将不同层的数据挤压到一起。
流形学习:
全称流形学习方法(Manifold Learning),从高维采样数据恢复低维流形结构。
分类:
流形学习方法是模式识别中的基本方法,分为线性流形学习算法和非线性流形学习算法,
非线性流形学习算法包括等距映射,拉普拉斯特征映射,局部线性嵌入等。
而线性方法则是对非线性方法的线性扩展,如主成分分析(PCA),多维尺度变换(MDS)等。
解释:
瑞士卷数据集是一个2D流形的例子。简单地说,一个2D流形是一个2D的形状,可以弯曲并旋转到一个更高的空间中。
更普遍地说,一个d维的流形是一个n-1维空间里的一部分(d < n),在本地类似于一个d维的超平面。
在这个瑞士卷例子中,d=2,n=3:它在本地类似一个2D平面,但是是在3维里卷成。
许多降维算法的方式是在训练实例上做流形建模,这个称为流形学习。
流形学习是一种常见的降维算法,它基于流形假设,即认为高维数据集通常接近于一个非常低维的流形结构。这意味着虽然数据在高维空间中有很多自由度,但它们实际上由较少的关键变量或维度所控制。
解决方案:
在做数据挖掘的时候,经常会遇到数据体量过大的情况,这种大体量往往会在两方面:
- 样本量过大(表现为行多);
- 样本特征过多(表现为列多);
好了,有点扯了,我来讲解PCA方法的使用。
PCA的步骤:
我就不一步一步讲了,太繁琐了,用简洁的语言,教复杂的学。
还记得我们的定义吧,PCA是通过线性线性变换,将数据映射到低维的子空间中的降维方法。
1.首先,确定降维之后的维度数;
2.找到一个对应维度的子空间,原数据映射到该空间下最大程度保留其方差;(就是调式维度数,让方差尽量达到最大. )
3.另外,还需要得到位置:从方差公式上我们可以看到,为了能够使得所有的方差计算更加公允
这会需要将每个特征减去它的均值,对于矩阵X而言,就是说:
通过减去均值,可以确保在计算主成分时,各个特征的方差都能够在相同的尺度上进行比较。这样可以避免某些特征的方差过大而主导了主成分的计算,从而更公平地评估每个特征对方差的贡献。
减去均值后的数据可以表示为X' = X - mean(X),其中X是原始数据,mean(X)是每个特征的均值向量。然后,对X'进行主成分分析,就可以得到每个主成分的方差,进而计算保留的方差百分比。
需要注意的是,在应用PCA之后,如果需要将数据还原到原始的特征空间中,需要将主成分乘以对应的标准差(即每个主成分的方差的平方根),并加上原始数据的均值。这样可以保持数据的原始尺度和分布。
在这里的 "公允" 指的是对各个特征在计算方差时的公正性和平等性。
总结:
1.所有数据中心化处理;
2.将数据映射到子空间中:
- 选择需要保留的信息量 or 选择维度;
- 通过线性变换,根据上述条件进行映射;
3.降维完毕;
中心化处理就是我们上面那个“每个特征减去它的均值”。
数据映射到子空间中,那这个数据就一定是通过调维度数之后,方差达到最大的数据。
那在这个过程中,我们干了什么,调维度参数,比较特征值方差,选最好。
那原理和步骤讲明白了,下面我们用Python代码来实现
python实现步骤:
首先,我们这边导入Scikit-learn库中的鸢尾花数据集。
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
#如遇中文显示问题可加入以下代码
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 鸢尾花的数据集
iris = datasets.load_iris()
iris感兴趣的,可以自己去弄着玩,数据是两个array,data是一个四维数据,下面用PCA进行降维。
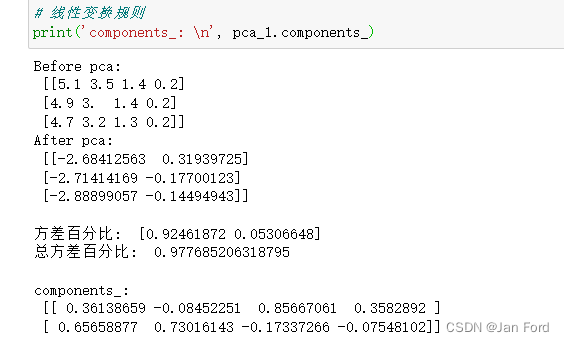
print('Before pca: \n', X[:3,:]) # 前三行,所有列
pca_1 = PCA(n_components=2) # 指定主成分数量初始化 将数据降为2维
X_red_1 = pca_1.fit_transform(X) # fit并直接得到降维结果
# 这里只展示前三行的结果以示对比
print('After pca: \n', X_red_1[:3, :],'\n')
# 查看各个特征值所占的百分比,也就是每个主成分保留的方差百分比
print('方差百分比: ', pca_1.explained_variance_ratio_)
# 当前保留总方差百分比;
print('总方差百分比: ',pca_1.explained_variance_ratio_.sum(),'\n')
# 线性变换规则
print('components_: \n', pca_1.components_)因为指定主成分数量数量为2,所以pca处理过后数据从四维变成了两维。
下面是一些参数上的用法:
-
fit_transform方法:这是PCA类中的方法,可以对原始数据进行降维处理。它首先使用fit方法计算出数据的主成分(特征向量),然后对原始数据进行线性变换,得到降维后的数据。这个方法可以合并fit和transform两个步骤,方便使用。 -
explained_variance_ratio_属性:这是PCA类中的属性,表示每个主成分保留的方差比例。它返回一个数组,数组的每个元素表示对应主成分保留的方差百分比。通过查看这个属性,我们可以了解每个主成分在总方差中的贡献程度。 -
explained_variance_ratio_.sum()方法:在PCA中,explained_variance_ratio_.sum()方法可以用来查看当前保留的总方差百分比。总方差百分比越高,说明保留的主成分越多,降维后的数据保留了较多的信息。 -
components_属性:这是PCA类中的属性,表示主成分(特征值)对应的特征向量。特征向量描述了数据的方向,在PCA中,它可以用来了解数据降维过程中的线性变换规则。同时,通过这个属性,也可以了解每个原始特征在新特征构建过程中的权重。
可视化:
plt.figure(figsize=(6,6))
for i in range(2):
plt.scatter(x=X_red_1[np.where(y==i),:][0][:,0], y=X_red_1[np.where(y==i),:][0][:,1], alpha=0.8, label='效果%s' % i)
plt.legend()
plt.show()
np.where(y==i):这部分代码会找出所有满足条件y==i的索引。y==i会返回一个布尔数组,表示数据中哪些位置的元素等于i。np.where()函数会返回满足条件的索引。
X_red_1[np.where(y==i), :]:这部分代码使用上一步得到的索引,从X_red_1中选取满足条件的数据点。:表示选取所有的列,保留所有的特征。
[0]:这部分代码会取出满足条件的数据点,并返回一个数组。由于我们只有一个条件,所以直接使用[0]来取出满足条件的数据点。
[:, 0]:这部分代码会取出满足条件的数据点的第一列,即x坐标。:,表示选取所有的行,0表示选取第一列。
[:, 1]:这部分代码会取出满足条件的数据点的第二列,即y坐标。:,表示选取所有的行,1表示选取第二列。效果图:
如果你降维数据是三维的,需要导入 Axes3D的包,普通的scatter绘制不了三维图。
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111, projection='3d')
for i in range(3):
ax.scatter3D(X_red_1[np.where(y==i),:][0][:,0], X_red_1[np.where(y==i),:][0][:,1], X_red_1[np.where(y==i), :][0][:, 2], alpha=0.8, label='效果%s' % i)
plt.legend()
plt.show()
这里除了导包外,改一下range,因为是三维,所以for结构多加一层。不用每一列赋值x,y。他是通过位置传参的方式。结果如下:
那第一种是指定降维个数,实质参数有待提高。
第二种
指定保留方差量初始化。这一种方法可以在降维后查看保留的维度数量
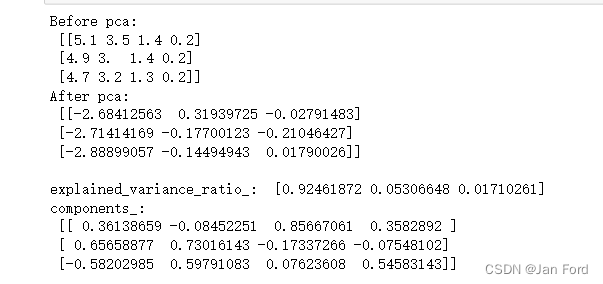
print('Before pca: \n', X[:3,:])
pca_2 = PCA(0.98)
# 后续的操作都一样,仅仅在初始化上有区别
X_red_2 = pca_2.fit_transform(X)
print('After pca: \n', X_red_2[:3, :],'\n')
print('explained_variance_ratio_: ', pca_2.explained_variance_ratio_)
print('components_: \n', pca_2.components_)这边就不是指定主成分个数了,而是指定保留0.98的信息量(方差)。让其自己找最好的降维个数。
那他这边就为了保留0.98的信息量,将数据降维成三类。
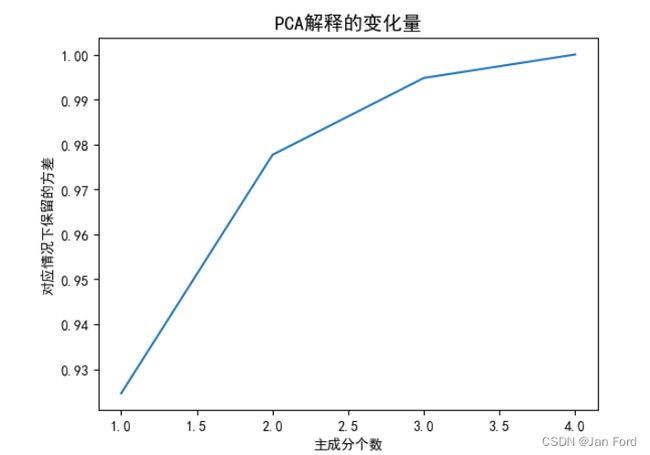
将其主成分个数可视化:
代码,如下:
# Fitting PCA
pca = PCA()
pca.fit_transform(X)
# 对所有的保留情况进行累加(1个主成分,2个,...直到和原本数据维度相同
explained_var = np.cumsum(pca.explained_variance_ratio_)
plt.plot(list(range(1, len(explained_var)+1)), explained_var)
plt.title('PCA解释的变化量', fontsize = 14)
plt.xlabel('主成分个数')
plt.ylabel('对应情况下保留的方差')
plt.show()Numpy库验证PCA可行度
回忆上面步骤:我们说第一步应该干嘛,“ 数据中心化处理 ”。
print("处理前: \n",X[:3, :])
# 数据中心化
for i in range(X.shape[-1]):
X[:, i] -= np.mean(X[:,i])
print("处理后: \n", X[:3,:])第二步,数据映射到子空间中。
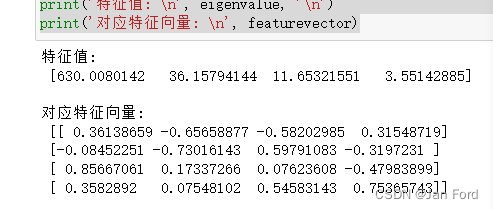
首先,求X 和 其转置矩阵的特征值 和 对应的特征向量。
# np.dot(X.T, X)表示计算矩阵X的转置与矩阵X的乘积,即X的转置乘以X。
# 这个结果将作为输入传递给np.linalg.eig()函数,该函数返回一个包含矩阵的特征值和特征向量的元组。
# eig()函数是NumPy线性代数模块(np.linalg)中的一个函数,用于计算一个方阵的特征值和特征向量。
eigenvalue, featurevector=np.linalg.eig(np.dot(X.T, X))
print('特征值: \n', eigenvalue, '\n')
print('对应特征向量: \n', featurevector)其次,选择最大的几个特征值,并得到对应的主成分,进行线性变换。
看图发现特征值前两列更大,保留两个维度进行降维,其次选择两个维度方便可视化。
下面进行对比验证:
# numpy 验证
dim_map = np.argsort(-eigenvalue)[:2] # 排序后,最大值在最前面,取前两列
vec = featurevector[:, dim_map] # 取出这两列所在的所有行,组成一个2维的特征向量矩阵
result_np = np.dot(X, vec) # 矩阵乘法运算,将原始数据 X 投影到由前两个主成分构成的特征空间中
# pca 实现
pca = PCA(n_components=2)
result_pca = pca.fit_transform(X)
print('pca结果:\n', result_pca[:3, :])
print('np结果:\n', result_np[:3, :])
print('numpy特征向量:\n', vec)
print('主成分对应的特征向量:\n', pca.components_)参数解析:
为什么 eigenvalue (特征值) 要设负号?
np.argsort函数默认按照从小到大的顺序返回索引.通过对特征值取负号,可以实现将特征值从大到小进行排序,因为负号会改变特征值的符号,使得原本较大的特征值变为较小的负数。
方差百分比
eigenvalue/eigenvalue.sum() # 对应的特征值除以所有特征值的总和
pca.explained_variance_ratio_ # PCA类中的属性,表示每个主成分保留的方差比例eigenvalue/eigenvalue.sum() 和 pca.explained_variance_ratio_ 是等价的,都表示每个主成分保留的方差比例。